Calculadora de velocidad angular

Esta calculadora de velocidad angular es una herramienta fácil de usar que da una respuesta inmediata a la pregunta "¿Cómo hallar la velocidad angular?". En el texto encontrarás varias fórmulas de velocidad angular, conocerás las distintas unidades de velocidad angular y, por último, ¡calcularás la velocidad angular de la Tierra!

¿Te has preguntado alguna vez qué relación hay entre la velocidad angular y la frecuencia angular? ¿O para qué se usa la velocidad angular? Sigue leyendo para averiguarlo y convertirte en un experto en el campo del movimiento circular.

La velocidad angular describe el movimiento de rotación de los cuerpos. Mide la rapidez con la que se mueven alrededor de un centro de rotación. Podemos pensar en dos tipos distintos de rotaciones. La primera describe el movimiento del centro de masas de un objeto alrededor de un punto concreto del espacio, que podemos tomar como origen punto de referencia. Algunos ejemplos son los planetas que se mueven alrededor del Sol o un automóvil que toma una salida en la autopista.

La segunda se refiere a la rotación del cuerpo alrededor de su propio centro de masa. Seguro que has visto a un jugador de baloncesto haciendo girar una pelota sobre su dedo.

En general, podemos decir que cuanto más rápido es el movimiento, mayor es la velocidad angular. Pero debemos pasar a las ecuaciones de velocidad angular que se describen en el siguiente apartado para definir algunos valores concretos.

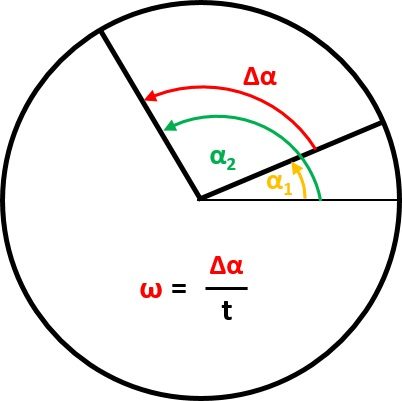
Esta calculadora de velocidad angular utiliza dos fórmulas diferentes de velocidad angular en función de tus parámetros de entrada.

La primera ecuación de la velocidad angular es análoga a la ecuación de la velocidad lineal:

donde $\alpha_1$ y $\alpha_2$ son dos valores de ángulos en un círculo, y $\Delta\alpha$ es su diferencia. $t$ es el tiempo en el que se produce el cambio de ángulo. Como puedes ver, para la velocidad normal, existe una relación del desplazamiento posicional en un periodo, mientras que aquí, utilizamos el ángulo en lugar de la distancia.

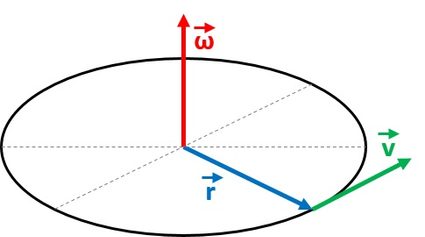
Podemos derivar la segunda fórmula de la velocidad angular a partir de la relación de la velocidad lineal y el radio utilizando el producto vectorial, o cruzado, que es:

Podemos reescribir esta expresión para obtener la ecuación de la velocidad angular:

donde todas estas variables son vectores, y $|r|$ denota la magnitud ddel vector radio, es decir, el valor absoluto del radio. En realidad, la velocidad angular es un pseudovector, cuya dirección es perpendicular al plano del movimiento de rotación.

Existen múltiples unidades de velocidad angular, y las que utilizamos en nuestra calculadora de velocidad angular se mencionan a continuación:

• rad/s o radianes por segundo - La definición procede directamente de la primera fórmula de la velocidad angular. Indica la magnitud de la rotación (o ángulo) que recorre el cuerpo en un tiempo determinado.

• RPM o revoluciones por minuto - Es la unidad que se encuentra con más frecuencia en la vida cotidiana. Con ella puedes describir la velocidad a la que gira una rueda o un motor. Puedes imaginar fácilmente la diferencia entre 10 y 100 RPM.

• Hz o hercios - Las mismas unidades que se utilizan para la frecuencia, pero rara vez se usan en el contexto de la velocidad angular. Es algo similar a las RPM, ya que nos indica cuántas rotaciones completas se realizan en un tiempo determinado. La diferencia es que antes, la unidad básica de tiempo era un minuto, y aquí es un segundo.

Naturalmente, todas estas unidades de velocidad angular se convierten entre sí mediante las siguientes relaciones:

1 RMP = 0.10472 rad/s = 0.01667 Hz

O al revés:

1 Hz = 6.283 rad/s = 60 RPM

Echa un vistazo a la definición de frecuencia angular:

donde $f$ es la frecuencia. Como vemos, se denota con la misma letra. Además, la unidad de la frecuencia angular es rad/s, precisamente la misma que para la velocidad angular. Así que puede surgir la pregunta: "¿Cuál es la diferencia entre velocidad angular y frecuencia angular?".

La respuesta es relativamente sencilla. La relación entre la frecuencia angular y la velocidad angular es análoga a la que existe entre la rapidez y la velocidad. La primera es una magnitud de la segunda; en otras palabras, la frecuencia angular es un escalar, mientras que la velocidad angular es un (pseudo)vector.

Solemos utilizar la frecuencia angular cuando hablamos de un movimiento armónico, cuyo ejemplo es un péndulo simple. Como puedes ver, el movimiento no tiene por qué estar representado por una rotación estándar, sino simplemente por un movimiento que repite periódicamente su posición. La velocidad angular, sin embargo, está estrictamente relacionada con el movimiento alrededor de algún punto. Por tanto, podemos decir que la frecuencia angular es una magnitud más general, y podemos utilizarla para describir una amplia gama de problemas físicos. En cambio, la velocidad angular sólo incluye el movimiento de rotación.

¿Qué tal si utilizamos nuestra calculadora de velocidad angular? ¡Calculemos la velocidad angular de la Tierra! En primer lugar, consideraremos la velocidad de giro. Sabemos que la Tierra realiza una rotación completa, respecto a las estrellas lejanas, en unas 23 h 56 min 4 s, lo que equivale aproximadamente a 23 934 h. La rotación completa es el ángulo 2π rad, por lo que la velocidad angular resultante es:

o $7.292 \times 10^{-5}\ \rm rad/s$ (utilizando la notación científica).

Ahora que conocemos la velocidad angular de giro de la Tierra, podemos evaluar su velocidad lineal en el ecuador. Para ello, necesitamos el radio de la Tierra, aproximadamente 6 371 km. Lo único que tenemos que hacer es insertar valores en la segunda fórmula de la velocidad angular:

Para calcular la velocidad lineal respecto al centro de la Tierra, basta con multiplicar este resultado por el coseno de la latitud de tu ciudad.

Por cierto, ¿te has preguntado alguna vez por qué los cohetes suelen lanzarse desde bases espaciales situadas cerca del ecuador y no desde los polos? Pues bien, cuanto más cerca del ecuador, mayor velocidad angular. Un impulso de casi 500 m/s al principio es una parte considerable de la velocidad objetivo. Así que mover el punto de partida lo más cerca posible del ecuador reduce la cantidad de combustible necesaria para acelerar el cohete.

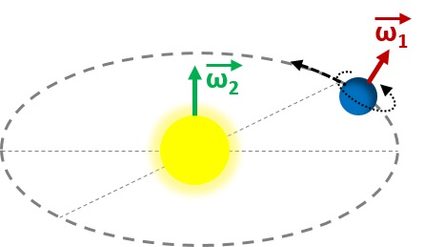
Después, podemos volver a pedir cómo hallar la velocidad angular de la Tierra, pero esta vez la orbital. Todos los cálculos son análogos, pero tenemos que cambiar el tiempo de 23 943 h a un año, que son unos 365.25 días. El cambio de ángulo es el mismo, la revolución completa.

y la velocidad lineal de la Tierra respecto al Sol (para el radio medio $\small 1.496\!\times\!10^8\ \rm km$) es:

Nos movemos muy rápido, ¿no te parece?

Múltiples magnitudes físicas están relacionadas con la velocidad angular, algunas de las cuales se enumeran a continuación:

1. Aceleración angular - Describe cómo cambia la velocidad angular con el tiempo. Cuanto mayor sea la diferencia de velocidades angulares, mayor será el valor de la aceleración angular. No dudes en comprobar cómo funciona en la realidad con nuestra calculadora de aceleración angular 🇺🇸.

2. Energía cinética rotacional - Es la medida de la energía en un movimiento circular. Como en el caso de la energía cinética lineal, la dependencia de la velocidad (angular) es cuadrática.

3. Fuerza centrípeta - Es la fuerza que te hace girar y mantenerte en movimiento circular; en un auto girando la ejercen los neumáticos. La tendencia a seguir en linea recta y no girar (primera ley de Newton) es la inercia, comúnmente llamada fuerza centrífuga aunque no es un fuerza real.

4. Efecto Coriolis - Hace que los objetos giren si residen en un cuerpo en rotación (por ejemplo, en la Tierra) en lugar de moverse en línea recta.

5. Sistema de poleas - No se trata de una magnitud física, técnicamente hablando, pero es un mecanismo interesante que tiene que ver con la velocidad angular. El sistema más sencillo consiste en dos poleas, normalmente con circunferencias o radios diferentes. Una correa las conecta, de modo que sus velocidades lineales son idénticas, pero como son de distintos tamaños, sus velocidades angulares cambian proporcionalmente.

   Sabiendo esto y teniendo algún motor con velocidad de rotación bien definida, podemos ajustar la velocidad angular del elemento de salida con buena precisión, simplemente ajustando su tamaño.

Unas cuantas reglas fundamentales nos hablan de las cantidades que se conservan en los sistemas aislados. Las más conocidas son la conservación de la energía y la conservación de momento. Junto a ellas, existe también la conservación del momento angular. Si pensamos en dos momentos en el tiempo, podemos escribir la regla como:

donde $I_1$ y $I_2$ son los momentos de inercia de las masas inicial y final. Estas magnitudes describen la distribución de la masa respecto a sus respectivos centros de rotación.

Podemos ver que, en esta situación, si el momento de inercia aumenta, la velocidad angular disminuye, y viceversa. ¿Cuáles son las consecuencias de este fenómeno?

Imaginemos que eres un patinador artístico. Cuando giras, posees cierta velocidad angular. Si tienes los brazos abiertos, el momento de inercia es relativamente grande. Entonces, acercas los brazos al resto del cuerpo. Como consecuencia, tu momento de inercia disminuye, así que como el momento angular global tiene que conservarse, tu velocidad angular aumenta: ¡significa que girarás más rápido! Esto no es magia, ¡sólo física!

Si no puedes / no te gusta patinar, puedes intentar verificar la regla con una silla de oficina que permita rotación. Sólo recuerda, ¡la seguridad es lo primero! Asegúrate de que haya espacio suficiente para hacer este experimento. Después, simplemente empieza a girar y observa cómo cambia tu velocidad angular cuando acercas y alejas los brazos de tu tronco. Además, puedes aumentar el efecto utilizando unas mancuernas. Como resultado, ¡puedes combinar ejercicio y diversión en una sola cosa!