Kombinationsrechner

Unser Kombinationsrechner hilft dir nicht nur dabei, die Anzahl der Kombinationen in einer Menge zu bestimmen, sondern zeigt dir auch jede einzelne mögliche Kombination (oder Permutation) deiner Menge an, bis zu einer Länge von 20 Elementen. Sei allerdings vorsichtig! Sogar unser Kombinationsgenerator könnte ein paar Sekunden brauchen, um so lange Terme zu finden. Wenn du dich fragst, wie viele verschiedene Kombinationen aus einer bestimmten Anzahl von Elementen und für einen bestimmten Stichprobenumfang möglich sind, probiere jetzt unseren Kombinationsrechner aus!

Wenn du dir noch nicht sicher bist, was eine Kombination wirklich ist, ließ dir den folgenden Artikel durch. Du findest hier eine Definition der Kombination und die Formel zur Kombinationenanzahl-Berechnung (mit und ohne Wiederholungen). Wir zeigen dir, wie du Kombinationen berechnen kannst, was die lineare Kombination und die Kombinationswahrscheinlichkeit ist. Schließlich sprechen wir über die Beziehung zwischen Permutation und Kombination. Kurz gesagt: Die Permutation berücksichtigt die Reihenfolge der Elemente, die Kombination nicht. Mehr Informationen findest du weiter unten!

Hast du dich schon einmal gefragt, wie hoch deine Chancen sind, den Hauptpreis in einer Lotterie zu gewinnen? Wie wahrscheinlich ist es, den zweiten Preis zu gewinnen? Um diese und ähnliche Fragen zu beantworten, musst du dich mit der Kombinatorik beschäftigen. Wir haben ein spezielles Tool für diese Art von Problemen erstellt. Unser Lotto Rechner 🇺🇸 schätzt nicht nur die Kombinationswahrscheinlichkeit für den Gewinn in einem beliebigen Lottospiel, sondern erklärt auch die dahinten stehende Formel. Probiere ihn aus! Du wirst herausfinden, wie groß (oder klein) deine Chancen tatsächlich sind.

Eine Kombination wird als die Anzahl der Weisen definiert, auf die du r Elemente aus einer Menge mit n verschiedenen Objekten auswählen kannst. Die Reihenfolge, in der du die Elemente auswählst, ist im Gegensatz zur Permutation nicht wichtig (eine ausführliche Erklärung dieses Problems findest du im Abschnitt Permutation und Kombination).

Die Suche nach jeder Kombination für eine Menge von Objekten ist ein rein mathematisches Problem. Du hast wahrscheinlich schon gelernt, wie man den größten gemeinsamen Teiler (ggT) oder das kleinste gemeinsame Vielfache (kgV) findet. Nun, eine Kombination ist eine ganz andere Geschichte. Mal sehen, wie kompliziert das sein kann.

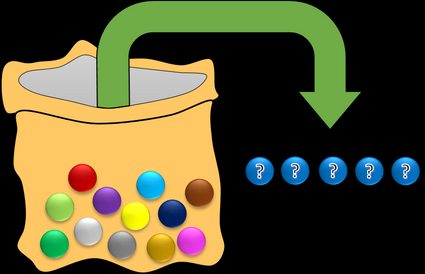
Stell dir einen Beutel mit zwölf Bällen vor, von denen jeder eine andere Farbe hat. Du wählst fünf Bälle nach dem Zufallsprinzip aus. Wie viele verschiedene Sätze von Bällen kannst du erhalten? Oder anders ausgedrückt: Wie viele verschiedene Kombinationen kannst du erhalten?

Mathematiker kennen die exakte Lösung für viele verschiedene Probleme, z. B. wie man die Quadratmeterzahl oder das Volumen berechnet. Gibt es einen ähnlichen Ansatz, um die Anzahl der Kombinationen im obigen Beispiel mit Bällen zu schätzen?

Zum Glück musst du nicht alle möglichen Kombinationen aufschreiben! Wie berechnest du dann die Kombinationen? Du kannst die folgende Formel verwenden, mit der du blitzschnell die Anzahl der Kombinationen ermitteln kannst:

wobei:

• $C(n, r)$ die Anzahl der Kombinationen,
• $n$ die Gesamtzahl der Elemente in der Menge und
• $r$ die Anzahl der Elemente, die du aus dieser Menge auswählst, ist.

Das Ausrufezeichen $!$ steht für die Fakultät. In unserem Fakultät Rechner 🇺🇸 findest du weitere Informationen zu diesem Thema. Der Ausdruck auf der rechten Seite ist auch als Binomialkoeffizient bekannt.

Wenden wir diese Gleichung auf unser Problem mit den bunten Kugeln an. Wir müssen bestimmen, wie viele verschiedene Kombinationen es gibt:

Du kannst das Ergebnis mit unserem Kombinationsrechner überprüfen. Er wird auch alle möglichen Kombinationen auflisten! Beachte aber, dass 792 verschiedene Kombinationen schon eine ganze Menge sind. Um zu vermeiden, dass zu viele Kombinationen generiert werden, haben wir den Kombinationsgenerator auf eine bestimmte maximale Anzahl von Kombinationen beschränkt (im Normalfall 2000). Du kannst diese Zahl im erweiterten Modus jederzeit ändern.

Wie aus der obigen Formel hervorgeht, ist die Anzahl der Kombinationen für die Auswahl nur eines Elements gleich $n$. Wenn du hingegen alle Elemente auswählen musst, gibt es nur eine Möglichkeit. Lass uns diese Eigenschaft anhand unseres Beispiels überprüfen. Du hast die Gesamtzahl der Objekte, die gleich $n = 12$ ist. Jeder Buchstabe in unserem Rechner steht für eine bestimmte Farbe eines Balls, z. B. A für rot, B für gelb, C für grün und so weiter. Wenn du nur ein einziges Element $r = 1$ aus dieser Menge auswählst, beträgt die Anzahl der Kombinationen $12$ – weil es 12 verschiedene Kugeln gibt. Wenn du aber $r = 12$ Elemente auswählst, gibt es nur $1$ mögliche Kombination, die jeden Ball enthält. Probiere es selbst mit dem Kombinationsrechner aus!

An dieser Stelle weißt du wahrscheinlich schon alles, was du über Kombinationen wissen solltest. Wenn du noch tiefer in das Thema eintauchen magst, behandeln wir in den nächsten Abschnitten die folgenden Aspekte: die Unterschiede zwischen Permutation und Kombination (die oft irrtümlich für dasselbe gehalten werden), die Kombinationswahrscheinlichkeit und die lineare Kombination.

Stell dir vor, du hast den gleichen Beutel mit bunten Bällen wie aus dem Beispiel des vorherigen Abschnitts. Auch hier wählst du die Bälle nach dem Zufallsprinzip aus, aber dieses Mal ist die Reihenfolge wichtig – es spielt eine Rolle, ob du den roten Ball als ersten oder als dritten auswählst. Nehmen wir ein konkretes Beispiel: Du wählst drei Kugeln mit den Namen R (rot), B (blau), G (grün). Es gibt sechs Permutationen dieser Menge (die Reihenfolge der Buchstaben bestimmt die Reihenfolge der ausgewählten Kugeln): RBG, RGB, BRG, BGR, GRB, GBR. Es gibt aber nur eine Kombination für die drei Kugeln. Das ist der entscheidende Unterschied.

Der Definition nach ist eine Permutation die Anordnung aller Elemente einer Menge in einer bestimmten Reihenfolge. Werden nicht alle Elemente der Menge verwendet, sprechen wir von einer Variation – der Anzahl der Möglichkeiten, auf die du r Elemente aus einer Menge mit n verschiedenen Objekten auswählen und anordnen kannst. Manchmal wird Variation auch Permutation von n Elementen zur r-ten Klasse genannt.

Vorsicht! Auf Englisch tendiert man dazu, den Begriff r-Permutation von n (r-permutation of n) anstatt von Variation (variation) zu verwenden. Somit umfasst im Englischen das Wort permutation beides die Variation (r ≠ n) und die Permutation (r = n).

Schau dir auch gerne unseren Permutationsrechner 🇺🇸 an.

Die Anzahl der möglichen Variationen (ohne Wiederholung) kann mit der folgenden Formel berechnet werden:

Erinnert dich diese Gleichung nicht an die Formel für die Berechnung der Kombinationen? Wenn du die Anzahl der Kombinationen kennst, kannst du die Anzahl der Variationen leicht berechnen:

Im erweiterten Modus unseres Rechners kannst du die Anzahl der Variationen ermitteln.

Du fragst dich vielleicht, wann du Variation oder Permutation statt Kombination verwenden solltest. Nun, das hängt davon ab, ob du die Reihenfolge berücksichtigen musst oder nicht. Nehmen wir zum Beispiel an, du hast einen Stapel mit neun Karten mit den Zahlen 1 bis 9. Du ziehst drei zufällige Karten und reihst sie auf dem Tisch auf, sodass eine dreistellige Zahl entsteht, z. B. 425 oder 837. Wie viele verschiedene Zahlen kannst du bilden?

Überprüfe das Ergebnis mit unserem Rechner! Und wie viele verschiedene Kombinationen gibt es?

Die Anzahl der Kombinationen ist immer kleiner als die Anzahl der Permutationen oder Variationen. In diesem Fall ist sie sechsmal kleiner (wenn du 84 mit $3! = 6$ multiplizierst, erhältst du 504). Das kommt daher, dass jede der drei Karten, die du auswählst, auf sechs verschiedene Arten neu angeordnet werden kann, genau wie im vorherigen Beispiel mit den drei Farbkugeln.

Um unsere Überlegungen zu Permutation, Variation und Kombination zu vervollständigen, müssen wir eine ähnliche Aufgabe besprechen, aber dieses Mal mit erlaubten Wiederholungen. Das bedeutet, dass du jedes Mal, nachdem du ein Element aus der Menge von n verschiedenen Objekten ausgewählt hast, dieses wieder in diese Menge zurücklegst. Im Beispiel mit den bunten Bällen nimmst du einen Ball aus dem Beutel, merkst dir, welchen du gezogen hast, und legst ihn zurück in den Beutel. Analog dazu wählst du aus den zweiten Beispiel mit den Karten eine Karte aus, schreibst dir die Nummer auf der Karte auf und legst sie zurück in den Stapel. Auf diese Weise kannst du z. B. zwei rote Kugeln in deiner Kombination haben oder die Zahl 228 durch deine Kartenwahl darstellen (Variation).

Du ahnst wahrscheinlich, dass beide Formeln sehr kompliziert werden. Trotzdem ist es nicht so kompliziert, wie den Alkoholgehalt deines selbstgebrauten Bieres zu berechnen. Im Falle der Variation vereinfacht sich die Gleichung sogar. Die Formel für die Kombination mit Wiederholung lautet wie folgt:

und für die Variation mit Wiederholung:

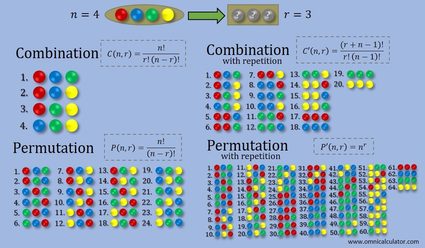
In der folgenden Abbildung haben wir die Unterschiede zwischen vier Arten der Auswahl von Objekten aus einer Menge zusammengefasst: Kombination, Kombination mit Wiederholung, Variation (auf Englisch auch Permutation) und Variation mit Wiederholung. In diesem Beispiel hast du vier Bälle in verschiedenen Farben und wählst drei davon aus. Bei der Auswahl mit Wiederholung kannst du eine der Kugeln mehrmals wählen. Wenn du das bei den Variationen machen willst, sei vorsichtig, denn es gibt Tausende von verschiedenen Mengen! Du kannst natürlich trotzdem berechnen, wie viele es sind (Permutationen findest du im erweiterten Modus).

Oft greifen wir zu Kombinatorik, um die Wahrscheinlichkeit eines bestimmten Ereignisses zu berechnen. Das oben abgebildete Beispiel sollte es leicht anschaulich machen: Du ziehst drei von vier bunten Kugeln aus einem Beutel. Angenommen, du möchtest wissen, wie hoch die Wahrscheinlichkeit ist, dass ein roter Ball darunter ist. Es gibt vier verschiedene Kombinationen, und die rote Kugel ist in drei von ihnen enthalten. Die gesuchte Wahrscheinlichkeit ist dann:

Wenn du drei zufällige Kugeln aus dem Beutel ziehst, wirst du in 75% der Fälle eine rote Kugel wählen. Um Wahrscheinlichkeiten auszudrücken, verwenden wir normalerweise das Prozentzeichen.

Nehmen wir an, du nimmst eine Kugel, schreibst auf, welche Farbe sie hat, und legst sie zurück in den Beutel, bevor du nochmal ziehst. Wie hoch ist die Wahrscheinlichkeit, dass du mindestens eine rote Kugel ziehst? In diesem Fall sprechen wir von „Kombination mit Wiederholung“. Auf dem Bild oben kannst du sehen, dass es insgesamt zwanzig Kombinationen gibt und die rote Kugel in zehn davon vorkommt, also:

Hat es dich überrascht? Gleich wird es klar. Wenn du die erste (z. B. die blaue) Kugel zurücklegst, kannst du sie nochmal als zweite und dritte Kugel ziehen. Die Chancen, eine rote Kugel zu ziehen, werden dadurch verringert. Ähnlich ist es mit den Variationen. Versuche, ein Problem mit dem Beutel mit bunten Kugeln zu lösen: Wie hoch ist die Wahrscheinlichkeit, dass die erste gezogene Kugel rot ist?

Vielleicht vertraust du uns nicht ganz und willst ein Experiment mit Kugelkombinationen durchführen. Du ziehst drei von vier Kugeln und überprüfst, ob eine rote Kugel dabei ist oder nicht (wie im ersten Beispiel dieses Abschnitts). Du wiederholst diesen Vorgang noch dreimal und bekommst die rote Kugel nur in einem von vier Fällen – $25\%$ der Fälle. Nach der Theorie hast du $75\%$ erwartet. Was ist passiert? Nun, so funktioniert die Wahrscheinlichkeitsrechnung! Hier kommt das Gesetz der großen Zahlen ins Spiel. Wenn du das Experiment oft (z. B. hundertmal) wiederholst, kommst du viel näher an die erwarteten $75\%$ heran.

Außerdem ist das Gesetz der großen Zahlen mit der Standardnormalverteilung eng verbunden, welche z. B. die Intelligenz oder die Größe von Menschen mit dem sogenannten p-Wert beschreiben kann. Willst du mehr erfahren? Der Rechner für die Normalverteilung könnte für dich interessant sein!

Hast du schon einmal von der Linearkombination gehört? Obwohl sie das Wort Kombination enthält, hat sie nicht viel mit dem gemeinsam, was wir bisher gelernt haben. Trotzdem werden wir versuchen, sie kurz zu erklären. Eine Linearkombination ist im Allgemeinen das Ergebnis einer Reihe von Termen, die mit einer Konstante multipliziert und dann aufaddiert werden. Im deutschen Sprachraum bezieht sich der Begriff normalerweise auf die Linearkombination von Vektoren (s. Punkt 1). Linearkombination wird in der Wellenphysik zur Vorhersage der Beugungsgittergleichung und sogar in der Quantenphysik wegen der de Broglie-Gleichung verwendet. Hier siehst du einige gängige Beispiele für Linearkombinationen:

1. Vektoren. Jeder Vektor in 3D kann in drei Einheitsvektoren $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ and $\^e_3 = (0,0,1)$ zerlegt werden. Zum Beispiel $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$. Dies bezeichnen wir als eine lineare Kombination.
2. Funktionen. Nehmen wir an, du hast zwei Funktionen $f(x) = \text{e}^x$ und $g(x) = \text{e}^{-x}$. Aus diesen beiden Funktionen kannst du Linearkombinationen bilden, die den hyperbolischen Sinus $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ oder den Kosinus $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$ beschreiben. Ähnliches kannst du auch mit dem normalen Sinus und Kosinus machen, aber du musst die imaginäre Zahl $i$ verwenden. Im letzten Abschnitt des Quadratwurzel Rechners schreiben wir mehr darüber.
3. Polynome. Du hast zum Beispiel drei Polynome $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ und willst die Funktion $q(x) = 2x^2 + x + 3$ als Linearkombination dieser Polynome ausdrücken. Das ist nicht für alle Polynome möglich, aber in diesem Fall $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.

Der grundlegende Unterschied zwischen Kombinationen und Variationen in der Mathematik ist, ob uns die Reihenfolge der Elemente wichtig ist oder nicht:

• Bei der Variation spielt die Reihenfolge eine Rolle, also ordnen wir die Gegenstände in der richtigen Reihenfolge an.
• Bei Kombinationen spielt die Reihenfolge keine Rolle, also wählen wir einfach eine Gruppe von Gegenständen aus einer größeren Sammlung aus.

Wenn du bereits eine Kombination hast und sie in eine Variation umwandeln möchtest, musst du der Menge der Gegenstände eine Anordnung geben, d. h. eine der möglichen Anordnungen für deine Menge wählen. Die Anzahl der Permutationen von r Gegenständen aus n Gegenständen ist also gleich der Anzahl der Kombinationen von r Gegenständen aus n Gegenständen, multipliziert mit der Anzahl der Anordnungen dieser r Gegenstände, d. h. mit r!.

Wenn du bereits eine Variation hast und sie in eine Kombination umwandeln möchtest, musst du die Reihenfolge entfernen, d. h. alle möglichen Anordnungen aus gleichen Elementen bestehenden Mengen als dasselbe Objekt betrachten. Daher ist die Anzahl der Kombinationen von r Gegenständen aus n Gegenständen gleich der Anzahl der Variation von r Gegenständen aus n Gegenständen, geteilt durch die Anzahl der Anordnungen dieser r Gegenstände, also durch r!.

Wenn das Wort aus sieben verschiedenen Buchstaben besteht, hast du 7! = 5040 Möglichkeiten, sie anzuordnen (Permutationen von sieben Elementen). Wenn jedoch einige Buchstaben mehr als einmal vorkommen, verringert sich die Anzahl der Möglichkeiten! Ein Beispiel:

• Wenn das Wort „ERDNUSS“ lautet, kommt das „S“ zweimal vor, also teilen wir 7! durch 2! = 2 und erhalten als Ergebnis 2520.
• Wenn das Wort „EXPRESS“ lautet, kommen „S“ und „E“ zweimal vor, also teilen wir 7! durch 2! ⋅ 2! = 4 und das Ergebnis ist somit 1260.
• Wenn das Wort „UNBEKANNT“ lautet, kommt das „N“ dreimal vor, also teilen wir 7! durch 3! = 6 und das Ergebnis ist 840.