Last updated: Apr 27, 2024

Brechungsgesetz Rechner

Q: Was ist das Brechungsgesetz?

Das Snelliussches Brechungsgesetz beschreibt die Beziehung zwischen dem Einfallswinkel θ₁ , dem Brechungswinkel θ₂ und den Brechungsindizes ( n ₁, n ₂) zweier Medien: n ₁sin(θ₁) = n ₂sin(θ₂). Das Brechungsgesetz ermöglicht es uns, den Biegungsgrad vorherzusagen, wenn das Licht von einem Medium in ein anderes wandert. Read more

Q: Gilt das Brechungsgesetz für alle Wellen?

Ja , du kannst das Snelliussches Brechungsgesetz auf alle isotropen Materialien , in allen Phasen der Materie anwenden. Das liegt daran, dass sich das Gesetz nur auf die Ausbreitung der Welle bezieht und nicht auf die Details der Welle selbst. Deshalb gilt es auch für Schallwellen. Read more

Q: Wie groß ist der Brechungswinkel, wenn der Einfallswinkel 10° beträgt?

7,5° . Nehmen wir an, ein Lichtstrahl tritt bei 10° ins Wasser ein. Um einen Brechungswinkel zu finden: Ermittle die Brechungsindizes von Luft, n ₁ =1, und Wasser, n ₂ = 1,33. Löse die Gleichung des Brechungsgesetzes für θ₂: sin(θ₂) = n ₁sin(θ₁)/ n ₂. Daher ist θ₂ = arcsin(1×sin(10°)/1,33) = 7,5°. Read more

Q: Wie kann ich den Brechungsindex von Glas mithilfe des Brechungsgesetz berechnen?

Angenommen, das Licht wandert von Luft durch Glas , dann beträgt der Einfallswinkel 30° und der Brechungswinkel 20°. Um den Brechungsindex zu berechnen, befolge diese Schritte: Bestimme den Brechungsindex von Luft: n ₁ = 1. Stelle das Snelliussches Brechungsgesetz um , um den Brechungsindex von Glas zu bestimmen: n ₂ = n ₁sin(θ₁)/sin(θ₂). Setze deine Werte ein : n ₂ = 1×sin(30°)/sin(20°) = 1,46. Read more

Q: Was sind die Grenzen des Brechungsgesetzes?

Die Grenze des Snelliussches Brechungsgesetzes liegt vor, wenn Licht auf die Oberfläche der Trennung zweier Medien auf oder durch die Lotlinie (senkrechte Linie) fällt. Wenn das Licht durch die Lotlinie fällt, ist der Einfallswinkel θ₁ gleich null . Nach dem Brechungsgesetz ist sin(θ₁) = sin(0°) = 0 , und der Brechungswinkel ist ebenfalls gleich null . Read more

Table of contents

Snellius-Gesetz der Lichtbrechung Bestimmung des Brechungswinkels – ein Beispiel Formel für den Grenzwinkel FAQs

Wenn Licht von einem Medium in ein anderes wandert, wird es gebeugt oder gebrochen. Mit dem Rechner für das Snelliussches Brechungsgesetz kannst du dieses Thema im Detail erforschen und die Prinzipien der Lichtbrechung verstehen. Lies weiter, um zu erfahren, wie das Snelliussches Brechungsgesetz formuliert ist und mit welcher Gleichung du den Brechungswinkel berechnen kannst. Der letzte Teil dieses Artikels ist der Formel und der Definition des Grenzwinkels gewidmet.

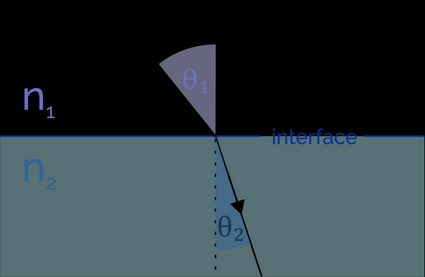
Snellius-Gesetz der Lichtbrechung

Das Snellius-Gesetz beschreibt, wie genau die Lichtbrechung funktioniert. Wenn ein Lichtstrahl in ein anderes Medium eintritt, ändern sich seine Geschwindigkeit und seine Wellenlänge. Der Lichtstrahl biegt sich entweder in Richtung der Lotlinie der beiden Mediengrenzen (wenn seine Geschwindigkeit abnimmt) oder von ihr weg (wenn seine Geschwindigkeit zunimmt). Der Brechungswinkel hängt von den Brechungsindizes der beiden Medien ab:

n_1 \sin(\theta_1) = n_2 \sin(\theta_2)

wobei:

$n_1$ der Brechungsindex des Mediums 1 (von dem der Strahl ausgeht) ist;
$n_2$ der Brechungsindex des Mediums 2 (in das der Strahl eintritt) ist;
$\theta_1$ der Einfallswinkel ist – der Winkel zwischen der Lotlinie und dem einfallenden Strahl;
$\theta_2$ der Brechungswinkel ist – der Winkel zwischen dem Lichtstrahl und dem Lot der Grenzfläche.

🔎 Im Ausbreitungsgeschwindigkeit Rechner 🇺🇸 kannst du überprüfen, wie sich die Geschwindigkeit des Lichts in verschiedenen Medien ändert.

Einige der Werte von $n_1$ und $n_2$ für gängige Medien findest du im Brechungsindex Rechner.

Im Allgemeinen gilt das Brechungsgesetz nur für isotrope Medien. Bei auftreffen auf anisotropen Medien, wie z. B. Kristalle, kann der Strahl in zwei Strahlen aufgeteilt werden.

Bestimmung des Brechungswinkels – ein Beispiel

Nehmen wir an, du möchtest den Brechungswinkel eines Lichtstrahls finden, der von Luft auf Glas trifft. Der Einfallswinkel beträgt 30°.

Finde den Brechungsindex von Luft. Dieser beträgt $1,000293$ .
Bestimme den Brechungsindex von Glas. Nehmen wir an, er ist gleich $1,50$ .
Stelle die Gleichung so um, dass die Unbekannte (der Brechungswinkel) auf der linken Seite steht: $\sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2}$ .
Setze die Werte in die Formel ein: $\sin(\theta_2) = \frac{1,\!000293 \sin(30\degree)}{1,\!50} = 0,\!333$ .
Finde den Bogensinus dieses Wertes: $\theta_2 = \arcsin(0,\!333) = 19,\!48 \degree$ .
Du kannst dir auch etwas Zeit sparen und einfach den Rechner für das Brechungsgesetz benutzen.

Formel für den Grenzwinkel

Manchmal erhältst du bei der Anwendung des Snelliussches Brechungsgesetz auf $\sin(\theta_2)$ einen Wert größer als 1. Das ist natürlich nicht möglich. Wenn das passiert, wird das gesamte Licht von der Grenze reflektiert (dieses Phänomen ist als Totalreflexion bekannt). Unser Rechner wird dich darauf hinweisen, wenn dieses eintritt.

Der höchste Einfallswinkel, bei dem das Licht nicht reflektiert wird, wird als Grenzwinkel bezeichnet. Der gebrochene Strahl wandert entlang der Grenze zwischen den beiden Medien. Das bedeutet, dass der Brechungswinkel 90° beträgt. Daher kannst du den Grenzwinkel mit der folgenden Gleichung ermitteln:

n_1 \sin(\theta_1) = n_2 \sin(\theta_2)

Nach der Vereinfachung: $n_1 \sin(\theta_1) = n_2 \cdot 1$ .

Stelle die Formel nach dem Einfallswinkel um, $\theta_1 = \arcsin(\frac{n_2}{n_1})$ .

🙋 Du willst mehr wissen? In unserem De Broglie-Wellenlänge Rechner 🇺🇸 erfährst du mehr über den Welle-Teilchen-Dualismus der Lichtbrechung.

FAQs

Was ist das Brechungsgesetz?

Das Snelliussches Brechungsgesetz beschreibt die Beziehung zwischen dem Einfallswinkel θ₁ , dem Brechungswinkel θ₂ und den Brechungsindizes (n₁, n₂) zweier Medien:
n₁sin(θ₁) = n₂sin(θ₂).
Das Brechungsgesetz ermöglicht es uns, den Biegungsgrad vorherzusagen, wenn das Licht von einem Medium in ein anderes wandert.

Gilt das Brechungsgesetz für alle Wellen?

Ja, du kannst das Snelliussches Brechungsgesetz auf alle isotropen Materialien, in allen Phasen der Materie anwenden. Das liegt daran, dass sich das Gesetz nur auf die Ausbreitung der Welle bezieht und nicht auf die Details der Welle selbst. Deshalb gilt es auch für Schallwellen.

Wie groß ist der Brechungswinkel, wenn der Einfallswinkel 10° beträgt?

7,5°. Nehmen wir an, ein Lichtstrahl tritt bei 10° ins Wasser ein. Um einen Brechungswinkel zu finden:

Ermittle die Brechungsindizes von Luft, n₁ =1, und Wasser, n₂ = 1,33.
Löse die Gleichung des Brechungsgesetzes für θ₂: sin(θ₂) = n₁sin(θ₁)/n₂.
Daher ist θ₂ = arcsin(1×sin(10°)/1,33) = 7,5°.

Wie kann ich den Brechungsindex von Glas mithilfe des Brechungsgesetz berechnen?

Angenommen, das Licht wandert von Luft durch Glas, dann beträgt der Einfallswinkel 30° und der Brechungswinkel 20°. Um den Brechungsindex zu berechnen, befolge diese Schritte:

Bestimme den Brechungsindex von Luft: n₁ = 1.
Stelle das Snelliussches Brechungsgesetz um, um den Brechungsindex von Glas zu bestimmen: n₂ = n₁sin(θ₁)/sin(θ₂).
Setze deine Werte ein: n₂ = 1×sin(30°)/sin(20°) = 1,46.

Was sind die Grenzen des Brechungsgesetzes?

Die Grenze des Snelliussches Brechungsgesetzes liegt vor, wenn Licht auf die Oberfläche der Trennung zweier Medien auf oder durch die Lotlinie (senkrechte Linie) fällt. Wenn das Licht durch die Lotlinie fällt, ist der Einfallswinkel θ₁ gleich null. Nach dem Brechungsgesetz ist sin(θ₁) = sin(0°) = 0, und der Brechungswinkel ist ebenfalls gleich null.