Rechner für den Winkel zwischen zwei Vektoren

Mit unserem Rechner für den Winkel zwischen zwei Vektoren lernst du schnell, wie du den Winkel zwischen zwei Vektoren bestimmen kannst. Dabei spielt es keine Rolle, ob deine Vektoren in 2D oder 3D sind. Egal, ob sie durch ihre Koordinaten oder Anfangs- und Endpunkte definiert sind – unser Rechner hat damit kein Problem. Probiere ihn einfach aus und sieh dir die Definitionen und Erklärungen weiter unten an; wenn du nach Formeln für den Winkel zwischen zwei Vektoren suchst, wirst du sie dort finden.

In diesem Abschnitt findest du die Formeln für den Winkel zwischen zwei Vektoren – und nur die Formeln. Wenn du verstehen möchtest, wie wir sie herleiten, lies direkt den nächsten Abschnitt, Wie findet man den Winkel zwischen zwei Vektoren?

Winkel zwischen zwei 2D-Vektoren

1. Durch Koordinaten dargestellte Vektoren:

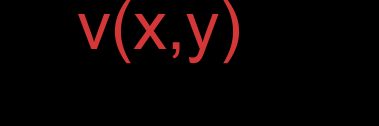
Für den Vektor $\boldsymbol a$:

und den Vektor $\boldsymbol b$:

ist der Winkel:

2. Durch Anfangs- und Endpunkte dargestellte Vektoren:

Für den Vektor $\boldsymbol a$:

und:

Vektor $\boldsymbol a$ ist gleich:

Für den Vektor $\boldsymbol b$:

und:

Vektor $\boldsymbol b$ ist also:

und:

Winkel zwischen zwei 3D-Vektoren

1. Durch Koordinaten dargestellte Vektoren:

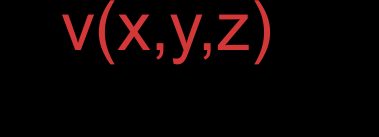
und:

dann der der Winkel:

Durch Anfangs- und Endpunkte dargestellte Vektoren:

Für den Vektor $\boldsymbol{a}$:

und:

Also:

Für den Vektor $\boldsymbol{b}$:

und:

Also:

Finde die endgültige Formel analog zur 2D-Version:

Es ist auch möglich, dass einer der Vektoren durch Koordinaten und der andere durch einen Anfangs- und Endpunkt definiert wird, das soll uns hier aber nicht weiter stören. Wichtig ist nur, dass dir unser Rechner für Winkel zwischen zwei Vektoren alle möglichen Kombinationen zur Verfügung stellt.

OK, der obige Absatz war für die TL;DR-Fans. Um die Formeln für den Winkel zwischen zwei Vektoren besser zu verstehen, schauen wir uns an, woher sie kommen:

1. Beginnen wir mit der grundlegenden geometrischen Formel zur Berechnung des Skalarprodukts 🇺🇸:

   Das Skalarprodukt ist das Produkt der Längen (Beträge) der Vektoren, multipliziert mit dem Kosinus des Winkels zwischen ihnen (hier bezeichnet mit $\alpha$):

2. Dann schreibe die Gleichung so um, dass du den Winkel erhältst:

   Teile durch das Produkt der Längen der Vektoren:

Finde die Umkehrfunktion des Kosinus (Arkuskosinus) für beide Seiten:

3. Erinnere dich daran, wie die Länge eines Vektors definiert wird:

   Da die Länge gleich der Quadratwurzel aus der Summe der Vektorkomponenten zum Quadrat ist, ergibt sich, dass:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ im 2D-Raum und

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ im 3D-Raum.

Hast du bemerkt, dass das die gleiche Formel ist, die auch im Abstandrechner angewendet wird? Sie stammt direkt aus der Geometrie. Das erklären wir dir ganz genau im Rechner für den Satz des Pythagoras.

4. Verwende die algebraische Formel für das Skalarprodukt (die Summe der Produkte der Vektorkomponenten) und setze die Beträge ein:

Im 2D-Raum:

Wir definieren die Vektoren $\boldsymbol{a}$ und $\boldsymbol{b}$ als:

und:

Im 3D-Raum:

Wir definieren die Vektoren $\boldsymbol{a}$ und $\boldsymbol{b}$ als:

und:

Dann:

Und das war’s!

Wenn deine Vektoren in einer anderen Form vorliegen (du kennst ihre Anfangs- und Endpunkte), musst du vorher einige Berechnungen durchführen. Das Ziel ist es, sie in die Standardvektorschreibweise zu bringen.

Wenn dein Beispielvektor durch den Anfangspunkt $A=(x_1, y_1)$ und den Endpunkt $B=(x_2, y_2)$ gegeben ist, dann kann er als Vektor $\boldsymbol{a}$ wie folgt dargestellt werden:

Du bist dir noch etwas unsicher? Kein Grund zur Sorge! Wir haben einige Beispielrechnungen vorbereitet, mit denen alles sonnenklar wird.

Angenommen, wir wollen den Winkel zwischen zwei Vektoren finden:

und $\boldsymbol{b}$ definiert als der Vektor zwischen den Punkten $A = (1, 1, 2)$ und $B = (-4, -8, 6)$.

Was müssen wir tun?

1. Zuerst Berechne den Vektor $\boldsymbol{b}$ anhand der Anfangs- und Endpunkte:

2. Finde dann das Skalarprodukt der Vektoren $\boldsymbol{a}$ und $\boldsymbol{b}$:

3. Als Nächstes bestimme die Länge der Vektoren:

Und:

4. Verwende schließlich die umgewandelte Skalarproduktgleichung:

Und das war’s! Du hast gerade den Winkel zwischen zwei 3D-Vektoren berechnet. Herzlichen Glückwunsch!

Wenn du noch mehr über verschiedene Elemente im Koordinatensystem lernen möchtest, empfehlen wir dir den Rechner für die mittlere Änderungsrate.

Wie funktioniert also unser Rechner für den Winkel zwischen zwei Vektoren? Folge dieser Schritt-für-Schritt-Anleitung:

1. Wähle deinen Vektorraum. Nehmen wir das gleiche Beispiel wie im vorherigen Abschnitt. Unsere Vektoren und Punkte haben drei Koordinaten, also müssen wir die Option 3D wählen.

2. Wähle die Darstellung des ersten Vektors. Der erste Vektor ist in Standardnotation, wir wählen also die Option Koordinatendarstellung.

3. Eingabe des ersten Vektors. Gib $x = 3,$ $y = 6,$ und $z = 1$ ein.

4. Wähle die Darstellung des zweiten Vektors. Diesmal wählen wird die Punktdarstellung.

5. Trag die Werte des zweiten Vektors ein. Gib $\boldsymbol A = (1,1,2)$ und $\boldsymbol B = (-4,-8,6)$ in die entsprechenden Felder ein.

6. Sobald du das letzte Feld ausfüllst, hat der Rechner den Winkel zwischen den zwei 3D-Vektoren ermittelt. In unserem Fall sind es $150,2 Grad$ – das ist natürlich dasselbe Ergebnis, das wir bei den manuellen Berechnungen erhalten haben.

Ein Vektor ist ein geometrisches Objekt, das sowohl einen Betrag als auch eine Richtung hat. Vektoren werden häufig verwendet, um physikalische Größen wie Kraft, Geschwindigkeit und Verschiebung darzustellen.

Der Winkel zwischen zwei Vektoren wird durch den umgekehrten Kosinus der Skalarprodukte der beiden Vektoren und das Produkt ihrer Längen definiert.

Um den Winkel zwischen zwei Vektoren in einem 2D-Raum zu berechnen:

1. Finde das Skalarprodukt der Vektoren.
2. Teile das Skalarprodukt durch die Länge des ersten Vektors.
3. Teile das Ergebnis durch die Länge des zweiten Vektors.

Mathematisch kann der Winkel α zwischen zwei Vektoren [x_a, y_a] und [x_b, y_b] wie folgt beschrieben werden:

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))]

Um den Winkel zwischen zwei Vektoren in einem 3D-Raum zu berechnen:

1. Finde das Skalarprodukt der Vektoren.
2. Teile das Skalarprodukt durch die Länge des ersten Vektors.
3. Teile das Ergebnis durch die Länge des zweiten Vektors.

Mathematisch kann der Winkel α zwischen zwei Vektoren [x_a, y_a, z_a] und [x_b, y_b, z_b] wie folgt beschrieben werden:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²))]