Umfang Rechner

Mit diesem Umfang-Rechner musst du dir keine Gedanken mehr über Umfangsberechnungen machen. Unten findest du die Formeln für den Umfang für zwölf verschiedene Formen sowie eine kurze Erinnerung daran, was der Umfang ist und wie dieser genau definiert wird. Lies weiter, probiere es aus oder schau dir den Zwillingsbruder dieses Rechners an — unseren umfassenden Flächeninhalt Rechner.

Der Umfang ist die Begrenzung einer geschlossenen geometrischen Figur. Er kann auch als äußerer Rand eines Flächeninhalts definiert werden, einfach als die längste durchgehende Gerade, die eine Form umgibt. Der englische Name „perimeter“ kommt aus dem Griechischen perimetros: peri bedeutet „um“ + metron, verstanden als „Maß“. Da es sich um die Länge des Umrisses einer Form handelt, wird sie in Entfernungseinheiten ausgedrückt — z. B. in Metern, Fuß, Zoll oder Meilen.

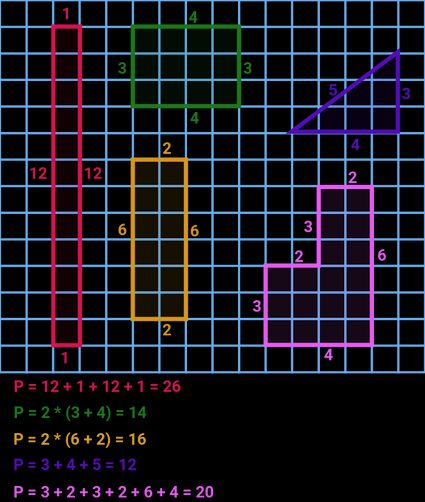
Normalerweise ist die einfachste und direkteste Methode, die Summe aller Seiten einer Form zu bestimmen. Es gibt jedoch Fälle, in denen es keine Seiten gibt (z. B. bei einer Ellipse, einem Kreis usw.) oder eine oder mehrere Seiten unbekannt sind. In diesem Abschnitt werden wir alle Gleichungen auflisten, die in diesem Umfang-Rechner verwendet werden.

Scrolle zu den nächsten Abschnitten, wenn du dich für eine bestimmte Form interessierst und eine Erklärung, eine Ableitung und ein Bild für jede der zwölf Formen in diesem Rechner sehen möchtest. Wir haben auch spezielle Tools für jede Form — gib einfach den Namen der Form in die Suchleiste oben auf dieser Seite ein.

Hier sind die Umfangsformeln für die zwölf geometrischen Formen in diesem Rechner:

• Quadrat Formel für den Umfang: $U = 4a$.

• Rechteck Umfangsformel: $U = 2(a + b)$.

• Dreieck Formeln für den Umfang:

  • $U = a + b + c$; oder
  • $U = a + b + \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$; oder
  • $P = a + \frac{a}{\sin(\beta + \gamma)} \times (\sin(\beta) + \sin(\gamma))$.

• Formel für den Umfang des Kreises: $U = 2\pi r$.

• Kreissektor Formel für den Umfang: $U = r(\alpha + 2)$ ($\alpha$ ist in Radiant);

• Ellipse Umfangsformel: $U = \pi\bigl[3(a + b) - \sqrt{(3a + b) \times (a + 3b)}\bigl]$;

• Quadrilateral / Trapez Umfangsformel: $U = a + b + c + d$.

• Parallelogramm Formeln für den Umfang:

  • $U = 2(a + b)$;
  • $U = 2a + \sqrt{2e^2 + 2f^2 - 4a^2}$; oder
  • $U = 2(b + h/\sin(\alpha))$.

• Rhombus Umfangsformeln:

  • $U = 4a$; oder
  • $U = 2\sqrt{e^2 + f^2}$.

• Drachen Umfangsformel: $U = 2(a + b)$.

• Kranz Umfangsformel: $U = 2\pi(R + r)$.

• Regelmäßiges Polygon Umfangsformel: $U = n \times a$.

Ein Quadrat hat vier Seitenlängen, die gleich lang sind. Um seinen Umfang zu berechnen, musst du nur die Seitenlänge mit $4$ multiplizieren:

Ob du es glaubst oder nicht, aber wir haben auch einen Umfang eines Quadrats Rechner 🇺🇸!

Die Formel für den Umfang eines Rechtecks ist fast so einfach wie die Gleichung für den Umfang eines Quadrats. Der einzige Unterschied ist, dass wir zwei Paare von gleich langen Seiten haben:

Die einfachste Formel zur Berechnung des Umfangs eines Dreiecks 🇺🇸 ist — wie üblich — die Addition aller Seiten:

Du hast aber nicht immer drei Seiten. Was kannst du dann tun? Nun, anstatt dich zu ärgern, kannst du den Kosinussatz Rechner benutzen, um die fehlende Seite zu finden:

Dies kann in die Formel für den Umfang aufgenommen werden:

Die andere Möglichkeit ist, den Sinussatz zu verwenden, wenn du eine Seite und die beiden Winkel, die an diese Seite angrenzen, hast:

und

Der Umfang des Dreiecks kann also wie folgt ausgedrückt werden:

Der Umfang eines Kreises hat einen besonderen Namen — er wird auch als Kreisumfang bezeichnet. Die bekannteste Formel für den Umfang eines Kreises verwendet nur eine Variable — den Radius des Kreises:

Hast du dich schon einmal gefragt, wie oft sich dein Rad auf einer Strecke von zehn Kilometern dreht? Dann ist das einer der Fälle, in denen du die Formel für den Umfang verwenden solltest. Gib den Radius deines Rads ein (die Hälfte des Raddurchmessers) und teile 10 Meilen durch den erhaltenen Umfang (aber vergiss die Umrechnung der Längeneinheiten nicht!). Wenn du es noch genauer haben möchtest, kannst du auch die Größe des Fahrradreifens angeben.

Die Berechnung des Umfangs eines Kreissektors mag knifflig klingen — ist es nur die Bogenlänge, oder ist es die Bogenlänge plus zwei Radien? Erinnere dich einfach an die Definition des Umfangs! Der Umfang eines Sektors ist die Summe der Längen aller Begrenzungen, also ist es letzteres:

wobei $\alpha$ in Radiant angegeben ist.

Obwohl die Formel für den Flächeninhalt einer Ellipse wirklich einfach und leicht zu merken ist, ist die Formel für den Umfang einer Ellipse die schwierigste aller hier aufgeführten Gleichungen. Wir haben uns entschieden, in diesem Umfangsrechner eine der Näherungen von Ramanujan zu verwenden:

Dabei ist $a$ der kleinstmögliche Radius und $b$ der größtmögliche Radius einer Ellipse. Die andere, genauere Näherung von Ramanujan lautet:

Es gibt auch eine einfachere Form, die eine zusätzliche Variable $h$ verwendet:

Das heißt:

Oder du kannst einfach unseren Rechner benutzen!

Wenn du den Umfang eines unregelmäßigen Trapezes berechnen möchtest, gibt es keine spezielle Formel — addiere einfach alle vier Seiten:

Vielleicht hast du es schon bemerkt, aber es ist die Formel für den Umfang jedes Vierecks.

Es gibt auch eine Option für bestimmte Trapeze, z. B. ein gleichschenkliges Trapez, für das du die Seiten $a$, $b$ und $c$ benötigst. Ein weiteres Beispiel ist ein rechteckiges Trapez, bei dem die Länge der Basen und eines Schenkels ausreicht, um den Umfang der Form zu bestimmen (um den letzten Schenkel zu finden, berechnen wir den Satz des Pythagoras).

In diesem Umfang-Rechner findest du drei Formeln zur Berechnung des Umfangs eines Parallelogramms:

1. Die einfachste, bei der du alle Seiten zusammenzählst:

2. Die Formel für den Umfang eines Parallelogramms, die eine Seite und Diagonalen erfordert

3. Der Umfang wird durch die Basis, die Höhe und einen beliebigen Parallelogrammwinkel angegeben.

Die Formel für den Umfang einer Raute ist kein großes Ding, also fassen wir uns kurz — es ist die gleiche Formel wie für den Umfang eines Quadrats!

Eine andere Lösung zur Ermittlung des Umfangs der Raute erfordert die Längen der Diagonalen:

Versuche, die Formel selbst herzuleiten. Du weißt, dass die beiden Diagonalen einer Raute senkrecht aufeinander stehen und sich halbieren, sodass du die Form in vier kongruente rechtwinklige Dreiecke unterteilen kannst. Jedes Dreieck hat Schenkel, die e/2 und f/2 lang sind — alles, was du tun musst, ist, die Hypotenuse des Dreiecks zu finden, die gleichzeitig die Seite der Raute ist. Multipliziere das Ergebnis dann mit vier, um den endgültigen Umfang einer Raute zu ermitteln.

Die Formel für den Umfang eines Drachens ist ziemlich einfach — du musst nur alle Seiten zusammenzählen:

Da der Umfang als Grenze definiert ist, müssen wir für einen Kranz den Umfang der beiden konzentrischen Kreise addieren:

In unserem Umfang-Rechner haben wir auch eine einfache Formel für den Umfang eines Regelmäßigen Polygons implementiert:

wobei $n$ die Anzahl der Polygonseiten ist. So kannst du z. B. den Umfang eines Fünfecks, Hexagons oder Achtecks berechnen.

Außerdem wird bei Polygonen mit bis zu 12 Seiten der Name des Polygons im Tool angezeigt. Wahnsinn!

Wenn du den Umfang eines beliebigen Polygons bestimmen möchtest, addiere die Längen aller Seiten:

$a_1$, $a_2$, ..., $a_n$ sind Seitenlängen, und $\sum$ ist das Summensymbol (von $i = 1$ bis $n$).

Oder verwende die Koordinaten der Scheitelpunkte:

Mit $x_{n+1}=x_1$ und $y_{n+1}=y_1$.