Last updated: May 06, 2024

Umfang Rechteck Rechner

Table of contents

Wie berechne ich den Umfang eines Rechtecks?Wie lautet die Formel für den Umfang eines Rechtecks?FAQs

Benutze unseren Rechner, wenn du schnell den Umfang eines bestimmten Rechtecks bestimmen möchtest. Versuche einige Werte einzugeben, oder lies weiter, um mehr über Rechtecke zu erfahren. Im folgenden Text erklären wir im Detail, wie man den Umfang eines Rechtecks mit 10 verschiedenen Formeln findet.

Das Rechteck hat vier rechte Winkel (4 ∙ 90° = 360°). Sein Name leitet sich von dem lateinischen Wort rectangulus ab, das rechter (rectus) Winkel (angulus) bedeutet. Die gegenüberliegenden Seiten des Rechtecks sind parallel zueinander und gleich lang. Ein Rechteck hat zwei Diagonalen, die sich in der Mitte des Rechtecks schneiden und gleich lang sind. Auf dem Bild unten siehst du ein typisches Rechteck mit markierten Parametern:

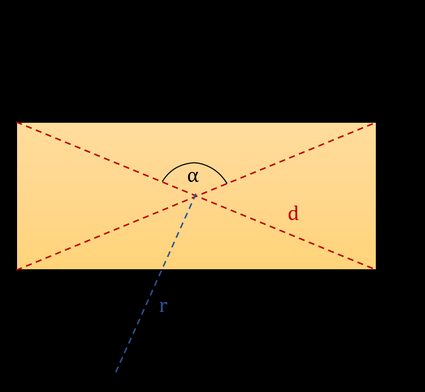
Ein Rechteck mit fünf grundlegenden Variablen und dem Umfang.

$a$ — Länge;
$b$ — Breite;
$\alpha$ — Winkel zwischen Diagonalen;
$r$ — Umkreisradius; und
$d$ — Diagonale.

Es gibt noch zwei weitere charakteristische Parameter, die nicht auf dem Bild zu sehen sind:

$A$ — Flächeninhalt; und
$U$ — Umfang.

Wenn dein Rechteck ein Quadrat ist (ein Viereck mit vier rechten Winkeln und vier gleich langen Seiten), dann kannst du immer den Umkreis des Rechtecks zeichnen, weil sein Mittelpunkt von allen vier Scheitelpunkten gleich weit entfernt ist. Außerdem liegt der Mittelpunkt dieses Kreises genau auf dem Schnittpunkt der zwei Diagonalen. Schau dir unseren Quadrat Umfang Rechner 🇺🇸 oder den Quadrat Diagonale Rechner an, wenn du spezielle Probleme mit Quadraten lösen musst!

Wie berechne ich den Umfang eines Rechtecks?

Ein Umfang ist eine Linie, die eine beliebige zweidimensionale Form umgibt. Du kannst sie dir wie einen Zaun vorstellen, der einen Hof oder einen Garten umgibt.

Wie berechne ich also den Umfang eines Rechtecks? Du musst die Längen der einzelnen Seiten addieren:

$U = a + b + a + b$

$U = 2 a + 2 b$

$U = 2 (a + b)$

Wie berechne ich den Umfang eines Rechtecks? – ein Rechteck mit den Seitenlängen a und b

Mit diesem Rechner für den Umfang eines Rechtecks kannst du Berechnungen in fast jeder Einheit durchführen, die du möchtest. Um mehr über Längeneinheiten zu erfahren, schau dir unseren Längen Umrechner an!

Wie lautet die Formel für den Umfang eines Rechtecks?

Um den Umfang in den obigen Gleichungen zu berechnen, haben wir zwei Seiten eines Rechtecks verwendet. In manchen mathematischen Fragestellungen sind jedoch andere Parameter gegeben. Wie berechnet man in diesen Fällen den Umfang eines Rechtecks? Die meisten dieser Aufgaben lassen sich mit dem Umfang-Rechner lösen. Bevor wir die entsprechenden Formeln aufschreiben, gibt es drei Grundgleichungen für den Flächeninhalt, die Diagonale und den Umkreisradius eines Rechtecks, die du dir merken solltest:

Flächeninhalt eines Rechtecks: $A = a ∙ b$ ;
Diagonale eines Rechtecks: $d = \sqrt{a^2 + b^2}$ ; und
Umkreisradius eines Rechtecks: $r = d/2$ .

Mit den obigen Gleichungen können wir nun verschiedene Formeln für den Umfang des Rechtecks ableiten, die von diesem Rechner verwendet werden:

Gegeben sind die Seitenlängen a und b:

\quad U = 2a + 2b

Gegeben sind die Seite a oder b und die Diagonale:

\quad U = 2a + 2\sqrt{d^2 - a^2} \\[8pt] \quad \text{oder}\\[8pt] \quad U = 2b + 2\sqrt{d^2 - b^2}

Gegeben sind die Seite a oder b und der Flächeninhalt:

\quad U = 2a + \frac{2A}{a} \\[8pt] \quad \text{oder}\\[8pt] \quad U = 2b + \frac{2A}{b}

Gegeben sind die Seite a oder b und der Winkel:

\quad U = 2a + \frac{2a}{\tan{\frac{\alpha}{2}}} \\[8pt] \quad \text{oder}\\[8pt] \quad U = 2b + \frac{2b}{\tan{\frac{\alpha}{2}}}

Gegeben sind die Seite a oder b und der Umkreisradius:

\quad U = 2a + 2\sqrt{4r^2 - a^2} \\[8pt] \quad \text{oder}\\[8pt] \quad U = 2b + 2\sqrt{4r^2 - b^2}

Gegeben sind die Diagonale und der Flächeninhalt:

\begin{align*} \quad U &= \sqrt{2d^2 + 2\sqrt{d^4 - 4A^2}} \\[8pt] &+ \sqrt{2d^2 - 2\sqrt{d^4 - 4A^2}} \end{align*}

Gegeben sind die Diagonale und der Winkel:

\quad U = 2d \left( \sin{\frac{\alpha}{2}} + \cos{\frac{\alpha}{2}} \right)

Gegeben sind der Flächeninhalt und der Winkel:

\quad U = 2\sqrt{\frac{A}{\tan{\frac{\alpha}{2}}}}\left( \tan{\frac{\alpha}{2}} + 1 \right)

Gegeben sind der Flächeninhalt und der Umkreisradius:

\begin{align*} \quad U &= \sqrt{8r^2 + 4\sqrt{4r^4 - A^2}} \\[8pt] &+ \sqrt{8r^2 - 4\sqrt{4r^4 - A^2}} \end{align*}

Gegeben sind der Winkel und der Umkreisradius:

\quad U = 4r \left( \sin{\frac{\alpha}{2}} + \cos{\frac{\alpha}{2}} \right)

Hinweis: Der Winkel $\alpha$ zwischen den Diagonalen steht vor der Länge wie in der ersten Abbildung. Denke auch daran, dass der Umfang eines Rechtecks davon ausgeht, dass eine Seitenlänge länger ist als die andere!

Hast du schon einmal vom Goldenen Rechteck gehört? Es ist ein besonderes Rechteck, dessen Seitenlängen im goldenen Schnitt stehen. Schau dir unseren Goldenes Rechteck Rechner an, um mehr über die Konstruktion von Goldenen Rechtecken zu erfahren! Wenn du etwas Allgemeines über den goldenen Schnitt lernen möchtest, ist unser Goldener Schnitt Rechner der richtige Ort, um damit zu beginnen.

FAQs

Wie lautet die Formel für den Umfang eines Rechtecks?

Hier findest du einige Formeln, mit denen du den Umfang eines Rechtecks berechnen kannst:

Umfang = 2 ∙ (Länge + Breite)

Wenn du den Flächeninhalt des Rechtecks und eine der Seiten kennst:

Umfang = (2 ∙ Länge) + ((2 ∙ Flächeninhalt) / Länge);

oder

Umfang = (2 ∙ Breite) + ((2 ∙ Flächeninhalt) / Breite).

Wie kann ich den Flächeninhalt eines Rechtecks in den Umfang umrechnen?

Um den Flächeninhalt in den Umfang eines Rechtecks umzurechnen, musst du neben dem Umfang auch mindestens eine der Seiten kennen.

Umfang = (2 ∙ Seite) + ((2 ∙ Flächeninhalt) / Seite)

Multipliziere die vorhandene Seite mit 2.
Multipliziere den Flächeninhalt des Rechtecks mit 2.
Dividiere das Ergebnis aus Schritt 2 durch die Länge der bekannten Seite.
Addiere die Ergebnisse aus Schritt 1 und 3.
Dein Ergebnis ist der Umfang eines Rechtecks.

Wie berechne ich den Umfang eines Rechtecks?

Um den Umfang eines Rechtecks zu bestimmen, befolge diese einfachen Schritte:

Notiere die Seitenlängen a und b des Rechtecks.
Addiere die vier Seitenlängen.
Multipliziere das Ergebnis aus Schritt 2 mit 2.
Das Ergebnis ist der Umfang des Rechtecks.

Wie berechne ich die Höhe eines Rechtecks?

Die Höhe eines Rechtecks ist eine der kurzen Seiten. Du kannst sie leicht berechnen, indem du einfach die Formel für den Flächeninhalt eines Rechtecks umstellst:

Fläche = Höhe ∙ Grundseite

Höhe = Flächeninhalt / Grundseite

Du musst also nur den Flächeninhalt eines Rechtecks durch die Grundseite teilen, und schon hast du die Höhe.

Wie groß ist der Umfang eines Rechtecks mit den Maßen 7×9 cm?

Der Umfang eines Rechtecks mit den Maßen 7 cm × 9 cm beträgt 32 cm.

Schauen wir uns an, wie wir so schnell auf die Antwort kommen:

Umfang = 2 × (Breite + Länge)

Umfang = 2 × (7 + 9)

Umfang = 2 × (16)

** Umfang = 32 cm**