Uhr Winkel Rechner

Der Uhr-Winkel-Rechner hilft dir, gängige Mathematikaufgaben zu lösen, wie z. B. „Wie berechne ich den Winkel der Uhrzeiger bei einer bestimmten Uhrzeit?“

Lernst du in der Schule gerade mehr über Winkel? Oder löst du vielleicht gerne Matheaufgaben zum Spaß und bist dir nicht sicher, ob du die richtige Antwort hast? ⏰

Lies weiter, um herauszufinden:

• Wie sehr sich die Zeiger analoger Uhren mit jeder Stunde und Minute bewegen;
• Wie man den Winkel zwischen den Uhrzeigern mit gesundem Menschenverstand findet;
• Wie man den Winkel mit Formeln findet; und
• Warum du mathematische Probleme mit Uhren immer visualisieren solltest.

Unser genialer Uhr-Winkel-Rechner hilft dir bei allen Fragen rund um die Uhrenwinkel. Also, los geht's! Wir haben keine Zeit zu verlieren.

Schau dir eine analoge Uhr an. Der kürzere Stundenzeiger macht in 12 Stunden eine volle Umdrehung. Das bedeutet, dass er sich jede Stunde um 30 Grad dreht.

360° / 12 = 30°

Aber der Stundenzeiger bewegt sich nicht nur einmal pro Stunde! Jede Minute dreht er sich um 0,5 Grad.

30° / 60 = 0,5°

Der Minutenzeiger dreht sich in 60 Minuten komplett. Er bewegt sich also jede Minute um 6 Grad.

360° / 60 = 6°

Um die Winkel zu bestimmen, die durch die Uhrzeiger entstehen, kannst du zwei Methoden anwenden:

1. Die erste Methode ist für diejenigen, die es vorziehen, mit Logik und ohne Formeln zur Lösung zu kommen.

2. Die zweite Methode ist für diejenigen, die gerne Formeln verwenden.

Wie du weißt, haben Computer keinen gesunden Menschenverstand, deshalb funktioniert unser Rechner für Uhrenwinkel dank Formeln. Da du wahrscheinlich kein Computer bist, kannst du die Methode verwenden, mit der du dich wohler fühlst.

Den Winkel zwischen dem Stunden- und Minutenzeiger zu bestimmen, ist einfach, wenn die Uhr eine volle Stunde hat. Der Minutenzeiger zielt auf die Zahl 12, also ist der Winkel gleich der Stunde multipliziert mit 30 Grad!

Lass uns das an einem Beispiel ausprobieren:

Beispiel 1. Wie groß ist der Winkel zwischen den Zeigern einer Uhr auf 4 Uhr?

Winkel zwischen den Uhrzeigern = 30° ∙ 4 = 120°

Der Winkel, den du suchst, ist 120°. Aber wusstest du, dass es zwei Winkel zwischen den Zeigern einer analogen Uhr gibt? Der Zweite füllt den Raum auf den anderen Seiten des Stunden- und Minutenzeigers aus. Du kannst ihn finden, indem du einen Winkel von einer vollen Umdrehung (360°) abziehst:

360° - 120° = 240°

Unser Uhr-Winkel-Rechner gibt dir zwei Winkel an, die im Uhrzeigersinn verlängert sind:

• Der Winkel vom Stunden- zum Minutenzeiger, hier — 240°; und
• Der Winkel vom Minuten- zum Stundenzeiger, hier — 120°.

Lass uns nun berechnen, wie man den Winkel zwischen den Uhrzeigern ohne Formeln bei einer schwierigeren Matheaufgabe zur Uhr findet:

Beispiel 2. Die Uhrzeit auf einer analogen Uhr lautet 10:14. Wie groß ist der Winkel zwischen den Zeigern?

Zeichne zunächst eine Uhr und markiere die charakteristischen Teile des Winkels.

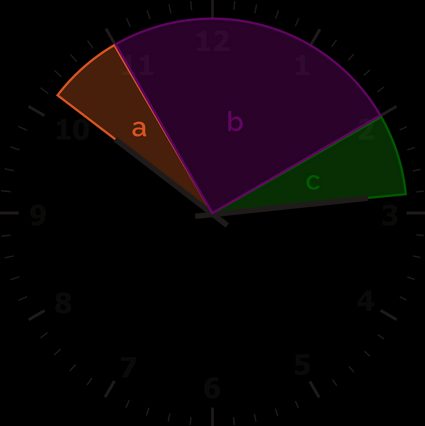
Beginnen wir mit der Bestimmung des Winkels b, da es am einfachsten ist, seine Größe zu berechnen. Er enthält 3 ganze Stunden (von Nummer 11 bis Nummer 2), ist also gleich groß:

b = 3 ∙ 30° = 90°

Dann haben wir die beiden verbleibenden Winkel mit a (neben dem Stundenzeiger) und c (neben dem Minutenzeiger) markiert.

Lass uns zuerst a finden. Wir sehen auf dem Bild, dass es kleiner als 30° ist. Der einfachste Weg, um a zu finden, ist zu sehen, wie weit der Stundenzeiger von der Zahl 10 entfernt ist. Der Winkel zwischen dem Stundenzeiger und der Zahl 10 auf einer Uhr ist 14 Minuten mal 0,5°.

14 ∙ 0,5° = 7°

Wie weit ist der Stundenzeiger also von der Zahl 11 entfernt?

a = 30° − 14 ∙ 0,5° = 30° − 7° = 23°

Zum Schluss müssen wir den Winkel c bestimmen. Der Minutenzeiger bewegt sich in vier Minuten von der Zahl zwei bis dorthin, wo er jetzt steht. Wir wissen bereits, dass er sich auch jede Minute um 6° bewegt. Also ist c gleich:

c = 4 ∙ 6° = 24°

Der Winkel zwischen dem Stundenzeiger und dem Minutenzeiger ist gleich:

Winkel zwischen den Uhrzeigern = 90° + 23° + 24° = 137°

Denke daran – es gibt zwei Winkel zwischen den Uhren! Der andere beträgt:

360° − 137° = 223°

Wie berechne ich den Winkel der Uhrzeiger in einem schwierigeren Beispiel?

1. Beginne wieder damit, eine Uhr zu zeichnen.

2. Markiere den Winkel zwischen dem Minutenzeiger und der 12-Uhr-Position. Wir wissen bereits, dass sich der Minutenzeiger jede Minute um 6° bewegt. Um also den Winkel zwischen dem Minutenzeiger und 12 Uhr zu berechnen, multiplizierst du die Anzahl der Minuten mit 6°.

   Winkel_Minuten = 6° ∙ Anzahl der Minuten

3. Markiere nun den Winkel zwischen dem Stundenzeiger und 12 Uhr. Denke daran, dass sich der Stundenzeiger mit jeder Minute bewegt. Um den richtigen Winkel zu finden, müssen wir also auch die Anzahl der Minuten berücksichtigen. Die Uhrzeiger-Winkel-Formel für den Stundenzeiger lautet also:

   Winkel_Stunden = 30° ∙ Anzahl der Stunden + 0,5° ∙ Anzahl der Minuten,

   denn der Stundenzeiger bewegt sich bei jeder vollen Stunde um 30° und um 0,5° pro Minute.

4. Schließlich musst du noch zwei Winkel zur Uhr finden. Um den Ersten zu finden, ziehst du den kleineren Winkel vom größeren ab. Mit anderen Worten: Finde den absoluten Wert 🇺🇸 der Differenz zweier Winkel:

   Erster Winkel zwischen den Uhrzeigern = |Winkel_Stunden – Winkel_Minuten|

• Wie bei der vorherigen Methode ist der andere Winkel elementar (zusammen ergeben sie einen vollen Kreis):

  Zweiter Winkel zwischen den Uhrzeigern = 360° – Erster Winkel zwischen den Uhrzeigern

Benutzen wir dieses Wissen, um eine Matheaufgabe zur Uhr zu lösen:

Beispiel 3. Finde den Winkel zwischen den Uhrzeigern um 8:23 Uhr.

• Bestimme zunächst den Winkel des Minutenzeigers. Verwende die Formel für den Minutenzeiger:

  Winkel_Minuten = 6° ∙ 23 = 138°

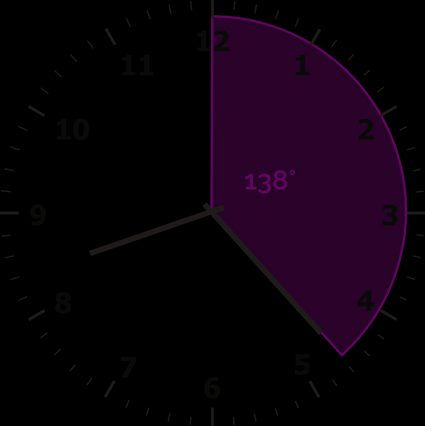
• Zweitens: Finde den Winkel des Stundenzeigers:

  Winkel_Stunden = 30° ∙ 8 + 0,5° ∙ 23 = 240° + 11,5° = 251,5°

• Subtrahiere die Werte zum Schluss:

  Der Winkel des Stundenzeigers ist größer als der Winkel des Minutenzeigers, also:

  Winkel_Stunden -Winkel_Minuten = 251,5° − 138° = 113,5°.

  Der erste Winkel zwischen den Uhrzeigern beträgt 113,5°.

• Finde bei Bedarf den zweiten Winkel:

  360° – Erster Winkel zwischen den Uhrzeigern = 360° − 113,5° = 246,5°

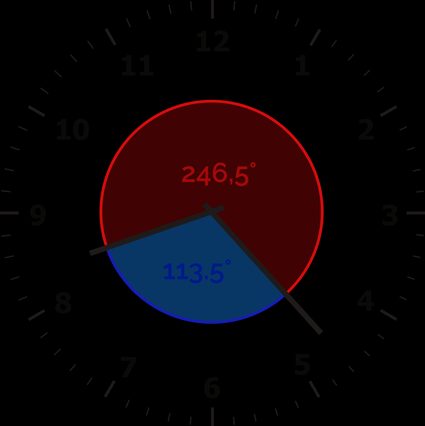
Wähle nun deine Lieblingsmethode und löse alle deine Matheaufgaben zur Uhr! Und vergiss nicht — du kannst deine Antwort jederzeit in unserem Uhr-Winkel-Rechner überprüfen! Bevor du loslegst, kannst du im Winkelumrechner 🇺🇸 lernen, wie du zwischen verschiedenen Einheiten zur Beschreibung von Winkeln umrechnen kannst.