Hexagon Rechner

Willkommen beim Sechseck-Rechner, einem praktischen Werkzeug für den Umgang mit jedem regelmäßigen Sechseck. Das Sechseck ist eine der am häufigsten auftretenden Formen in der Natur, von Bienenwabenmustern bis hin zu Sechseckfliesen für Spiegel – seine Einsatzmöglichkeiten sind schier endlos. Hier erklären wir nicht nur, warum das 6-seitige Vieleck so beliebt ist, sondern auch, wie die Seiten eines Sechsecks richtig gezeichnet werden. Außerdem beantworten wir die Frage „Was ist ein Sechseck?”, indem wir uns seine Definition anschauen.

Mit unserem Sechseck-Rechner kannst du viele geometrische Eigenschaften und Berechnungen erforschen, z. B. wie der Flächeninhalt eines Sechsecks ermittelt wird. Zudem zeigen wir dir, wie du den Rechner nutzen kannst, um jede Analyse, welche diese 6-seitige Form betrifft, zu vereinfachen.

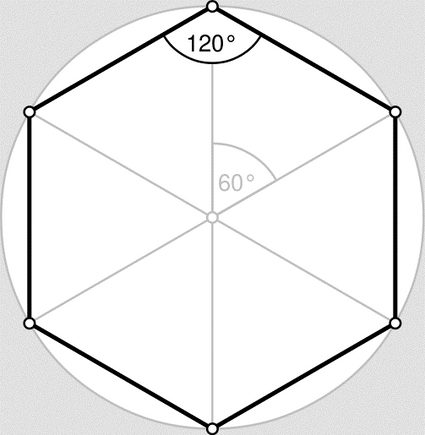
Es sollte keine Überraschung sein, dass das Sechseck (auch bekannt als Hexagon oder 6-seitiges Polygon) genau sechs Seiten hat. Diese Tatsache trifft auf alle Sechsecke zu, denn sie ist ihr bestimmendes Merkmal. Bis auf das regelmäßige Sechseck, bei dem alle Seiten gleich lang sind, kann die Länge der Seiten sogar innerhalb desselben Sechsecks variieren.

Wir betrachten dies genauer, wenn wir uns in den folgenden Abschnitten damit beschäftigen, wie der Flächeninhalt eines Sechsecks bestimmt wird. Für den Moment genügt es zu sagen, dass das regelmäßige Sechseck das häufigste unter den sechsseitigen Polygonen ist und in der Natur am häufigsten vorkommt.

Ein ganzer Abschnitt wird sich mit den wichtigen Eigenschaften des regelmäßigen Sechsecks befassen. Zuerst müssen wir uns aber mit der Frage „Was ist ein Sechseck?” beschäftigen. Die Antwort wird uns helfen, die Berechnungen und Tricks zu verstehen, mit denen wir die Fläche eines Sechsecks ermitteln können. Diese Tricks beinhalten die Verwendung der Formeln anderer Polygone wie Quadrate, Dreiecke und sogar Parallelogramme.

Wie wir bereits erwähnt haben, müssen bei einem regelmäßigen Sechseck alle Seiten gleich lang und alle Innenwinkel gleich groß sein. In diesem Fall ist die Berechnung des Umfangs eines Sechsecks so einfach, dass du nicht einmal den Umfang von Vielecken Rechner 🇺🇸 brauchst. Rechne einfach:

• Umfang = 6 ∙ Seite

Die Winkel eines beliebigen Sechsecks können jeden beliebigen Wert haben, sie müssen aber alle zusammen 720º ergeben (du kannst sie ganz einfach mit unserem Winkel Rechner 🇺🇸 in andere Einheiten umrechnen). Da die Definition des regelmäßigen Sechsecks verlangt, dass alle Winkel gleich groß sind, folgt daraus, dass in einem solchen Sechseck jeder einzelne Winkel 120º betragen muss. Diese Tatsache erweist sich als äußerst wichtig, wenn wir über die Beliebtheit der Sechseckform in der Natur sprechen. Sie wird auch bei der Erklärung der Formel und der Berechnung des Flächeninhaltes eines regelmäßigen Sechsecks hilfreich sein.

Wir schauen uns jetzt an, wie der Flächeninhalt eines Sechsecks mit verschiedenen Rechenwegen und Tricks ermitteln werden kann. Am einfachsten ist es, unseren Sechseck-Rechner zu verwenden, der ein eingebautes Tool zur Flächenumrechnung enthält. Für diejenigen, die wissen wollen, wie der Flächeninhalt handschriftlich berechnet wird, erklären wir, wie der Flächeninhalt eines regelmäßigen Sechsecks mit und ohne die Formel für den Flächeninhalt ermittelt werden kann. Die Formel für den Flächeninhalt eines Vielecks ist immer dieselbe, egal wie viele Seiten es hat, solange es ein regelmäßiges Vieleck ist:

• Fläche = Apothema ∙ Umfang / 2

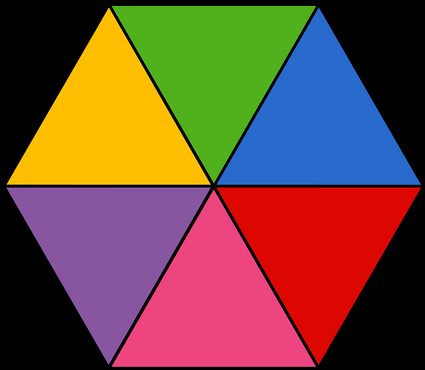
Zur Erinnerung: Das Apothema ist der Abstand zwischen dem Mittelpunkt einer Seite und dem Mittelpunkt des Vielecks. Du kannst sie als die Höhe des gleichseitigen Dreiecks betrachten, das aus einer Seite und zwei Radien des Sechsecks gebildet wird (jede der farbigen Flächen in der Abbildung oben). Alternativ kannst du dir das Apothema auch als den Abstand zwischen dem Mittelpunkt und einer beliebigen Seite des Sechsecks vorstellen, da der euklidische Abstand durch eine senkrechte Linie definiert ist.

Wenn du dich nicht an die Formel erinnerst, kannst du dir das sechseckige Polygon auch als eine Sammlung von sechs Dreiecken vorstellen. Bei einem regelmäßigen Sechseck sind diese Dreiecke gleichseitige Dreiecke. Diese Tatsache macht es viel einfacher, ihre Fläche zu berechnen, als wenn sie gleichschenklige Dreiecke oder sogar 45 45 90 Dreiecke wie im Falle eines Quadrats wären.

Bei einem regelmäßigen Dreieck sind alle Seiten gleich lang, sie haben die Länge der Seite des Sechsecks, das sie bilden. Wir nennen diese Länge a. Die Höhe eines Dreiecks berechnet sich aus h = √3/2 ∙ a, was in diesem Fall die Länge des Apothemas ist. Wir erinnern dich daran, dass √ die Quadratwurzel ist. Damit können wir mit den Berechnungen beginnen:

• A₀ = a ∙ h / 2
• = a ∙ √3/2 ∙ a / 2
• = √3/4 ∙ a²

Dabei bedeutet A₀ die Fläche jedes der gleichseitigen Dreiecke, in die wir das Sechseck unterteilt haben. Nachdem wir diese Fläche mit sechs multipliziert haben (weil wir 6 Dreiecke haben), erhalten wir die Formel für die Fläche des Sechsecks:

• A = 6 ∙ A₀ = 6 ∙ √3/4 ∙ a²

• A = 3 ∙ √3/2 ∙ a²

• = (√3/2 ∙ a) ∙ (6 ∙ a) /2

• = Apothema ∙ Umfang /2

Wir hoffen, du kannst sehen, wie wir auf die gleiche Formel für die Fläche des Sechsecks kommen, die wir bereits erwähnt haben.

Wenn du abenteuerlustig bist, kannst du auch mit anderen Formen herumexperimentieren. Nimm zum Beispiel an, dass du das Sechseck in der Mitte teilst (von Scheitelpunkt zu Scheitelpunkt). In diesem Fall erhältst du zwei Trapeze und kannst die Fläche des Sechsecks als Summe der beiden Trapeze berechnen. Du könntest auch zwei benachbarte Dreiecke miteinander verbinden, um insgesamt 3 verschiedene Rauten zu konstruieren und den Flächeninhalt jeder einzelnen zu berechnen. Du kannst das Sechseck sogar in ein großes Rechteck (unter Verwendung der kurzen Diagonalen) und 2 gleichschenklige Dreiecke zerlegen!

Probiere ruhig mit verschiedenen Formen und Rechnern herum, um zu sehen, welche anderen Tricks dir einfallen. Versuche, nur rechtwinklige Dreiecke zu verwenden, um die Fläche eines Sechsecks zu berechnen!

Ein Sechseck hat insgesamt 9 Diagonalen – drei davon sind lange Diagonalen, die den Mittelpunkt kreuzen, die anderen sechs sind die sogenannte „Höhe” des Sechsecks.
Unser Sechseck-Rechner erspart dir die mühsame Berechnung der Längen der Diagonalen des Sechsecks. Hier siehst du, wie du die beiden Arten von Diagonalen berechnest:

• Lange Diagonalen – Sie gehen immer durch den Mittelpunkt des Sechsecks. Wie du auf dem Bild oben sehen kannst, ist die Länge einer solchen Diagonale gleich zwei Kantenlängen:

  D = 2 ∙ a

• Kurze Diagonalen – Sie kreuzen den Mittelpunkt nicht. Sie werden konstruiert, indem man zwei Scheitelpunkte verbindet und genau einen dazwischen frei lässt. Ihre Länge entspricht d = √3 ∙ a.

Ein weiteres Paar von Werten, die in einem Sechseck wichtig sind, sind der Umkreisradius und der Inkreisradius. Der Umkreisradius ist der Radius des Kreises, der durch alle Eckpunkte des regelmäßigen Sechsecks geht. Der Inkreisradius ist der Radius des größten Kreises, der vollständig im Sechseck enthalten ist.

• Umkreisradius: Um den Radius eines Umkreises zu bestimmen, musst du den Abstand zwischen dem Mittelpunkt des Sechsecks (der auch der Mittelpunkt des Kreises ist) und einem der Scheitelpunkte bestimmen. Er ist gleich R = a.

• Inkreisradius: Der Radius eines Kreises, der in einem regelmäßigen Sechseck vollständig enthalten ist, entspricht gleich der Hälfte seiner Höhe, was auch dem Apothema entspricht: r = √3/2 ∙ a.

Jetzt werden wir eine praktischere und weniger mathematische Welt erkunden: wie du ein Sechseck zeichnest. Für ein zufälliges (unregelmäßiges) Sechseck ist die Antwort einfach: Zeichne eine beliebige 6-seitige Form so, dass sie ein geschlossenes Polygon ergibt und du bist fertig. Für ein regelmäßiges Sechseck ist das natürlich nicht ganz so einfach. Wir müssen sicherstellen, dass alle Seiten gleich lang sind.

Um ein perfektes Ergebnis zu erzielen, brauchst du einen Zeichenzirkel. Stelle deinen Zirkel auf den gewünschten Radius ein und zeichne zuerst einen Kreis und ziehe die Mittellinie durch ihn. Nimm nun einen Schnittpunkt des Kreises mit der Mittellinie als Mittelpunkt eines neuen Kreises und ziehe, mit demselben Radius, einen Halbkreis durch den Mittelpunkt des ersten Kreises. Ziehe den dritten Kreis, auf der gegenüberliegenden Seite auf die gleiche Weise. Am Ende hat dein erster Kreis 6 Schnittpunkte. Wenn du diese durch Geraden verbindest, erhältst du ein regelmäßiges Sechseck. Einen ähnlichen Prozess kannst du in der Animation oben sehen.

Mit dem Sechseck-Rechner kannst du mehrere interessante Parameter des Sechsecks bestimmen. Die Verwendung dieses Rechners ist so einfach, wie es nur geht, da nur einer der Parameter benötigt wird, um alle anderen zu berechnen. Der Rechner enthält auch ein eingebautes Umrechnungstool für Längeneinheiten für jeden dieser Parameter.

Wir haben alle Parameter des Rechners besprochen, aber der Klarheit und Vollständigkeit halber gehen wir nochmal kurz auf sie ein:

• Fläche – 2-D-Fläche, die von der Sechseckform umschlossen wird;
• Seitenlänge – Abstand von einem Scheitelpunkt zum darauffolgenden;
• Umfang – Summe der Längen aller Sechseckseiten;
• lange Diagonale – Abstand von einem Scheitelpunkt zum gegenüberliegenden Scheitelpunkt;
• kurze Diagonale – Abstand zwischen zwei Scheitelpunkten, zwischen denen nur ein weiterer Scheitelpunkt liegt;
• Radius des Umkreises – Abstand vom Mittelpunkt zu einem Scheitelpunkt (entspricht dem Radius des Sechsecks) und
• Radius des Inkreises – gleich dem Apothema.

Jedes Problem lässt sich besser an einer praktischen Anwendung verstehen und Sechsecke sind definitiv eines der meistgenutzten Vielecke der Welt. Die einfachste (und wahrscheinlich am wenigsten aufregende) Anwendung sind sechseckige Fliesen für Fußböden. Das Sechseck ist eine hervorragende Form, weil sie perfekt ineinander passen, und so jede gewünschte Fläche abdecken können. Wenn dich eine solche Verwendung interessiert, empfehlen wir dir den Rechner für Bodenbeläge und den Quadratfuß Rechner 🇺🇸, sie sind exzellente Werkzeuge für diesen Zweck.

Der nächste Fall ist für alle Polygone typisch, aber trotzdem interessant zu sehen. In der Fotografie hat die Öffnung des Sensors fast immer eine polygonale Form. Dieser Teil der Kamera wird Blende genannt und bestimmt viele Eigenschaften und Merkmale der Bilder, die von einer Kamera produziert werden. Die verblüffendste Eigenschaft ist die Form sehr heller (punktförmiger) Objekte, die auf den Effekt des Beugungsgitters zurückzuführen ist, wie in der Abbildung oben zu sehen ist.

Eine der wertvollsten Anwendungen von Sechsecken in der modernen Zeit, die eng mit der Fotografie zusammenhängt, finden wir in der Astronomie. Eines der größten Probleme bei der Beobachtung entfernter Sterne ist, dass sie am Nachthimmel nur sehr schwach zu sehen sind. Das liegt daran, dass sie zwar sehr helle Objekte sind, aber so weit weg sind, dass uns nur ein winziger Teil ihres Lichts erreicht; mehr darüber erfährst du in unserem Leuchtkraft Rechner 🇺🇸. Hinzu kommt, dass ihr Licht aufgrund von relativistischen Effekten (ähnlich wie Zeitdilatation und Längenkontraktion) mit weniger Energie auf der Erde ankommt, als es ausgestrahlt wurde. Dieser Effekt wird Rotverschiebung genannt.

Das Ergebnis ist, dass wir eine winzige Menge an Energie mit einer größeren Wellenlänge erhalten, als uns lieb ist. Die beste Möglichkeit, dem entgegenzuwirken, ist es, Teleskope so groß wie möglich zu bauen. Das Problem ist, dass es fast unmöglich ist, eine einteilige Linse oder einen einteiligen Spiegel zu bauen, der größer als ein paar Meter ist, ganz zu schweigen von den logistischen Problemen. Die Lösung besteht darin, einen modularen Spiegel aus sechseckigen Kacheln zu bauen, wie du sie auf den Bildern oben sehen kannst.

Der Bau eines so großen Spiegels verbessert die Winkelauflösung des Teleskops und den Vergrößerungsfaktor aufgrund der geometrischen Eigenschaften eines „Cassegrain-Teleskops”. Wir können also sagen, dass wir dank regelmäßiger Sechsecke besser, weiter und klarer ins Weltall sehen können, als wir es mit einteiligen Linsen oder Spiegeln jemals hätten tun können.

Wusstest du, dass es auch sechseckige Steppdecken gibt? Entdecke mehr mit Omni's Sechseckige Steppdecke Rechner 🇺🇸!

Das Wabenmuster besteht aus regelmäßigen Sechsecken, die nebeneinander angeordnet sind. Sie füllen die gesamte Fläche, die sie überspannen, vollständig aus, sodass es keine Löcher zwischen ihnen gibt. Dieses Wabenmuster kommt nicht nur in Honigwaben vor (Überraschung!), sondern auch an vielen anderen Stellen in der Natur. Es ist sogar so beliebt, dass man sagen könnte, dass es die Standardform ist, wenn Kräfte gegeneinander wirken und die Formung von Kugeln aufgrund der Natur des Problems nicht möglich ist.

Von Bienenstöcken über Gesteinsrisse bis hin zur organischen Chemie (sogar in den Bausteinen des Lebens: den Proteinen) sind regelmäßige Sechsecke die am häufigsten vorkommende Vieleckform der Natur. Und dafür gibt es einen Grund: die Sechseck-Winkel. Der 120º-Winkel ist der mechanisch stabilste von allen und zufälligerweise auch der Winkel, in dem sich die Seiten an den Scheitelpunkten treffen, wenn wir Sechsecke nebeneinander anordnen. Eine ausführliche Beschreibung der Bedeutung und der Vorteile regelmäßiger Sechsecke findest du in diesem Youtubevideo.

Die Art und Weise, auf welche die 120º-Winkel die Kräfte (und damit auch die Belastung) auf zwei der Sechseck-Seiten verteilen, macht das Sechseck zu einer sehr stabilen und mechanisch effizienten geometrischen Form. Das ist ein wichtiger Vorteil des Sechsecks. Eine weitere wichtige Eigenschaft regelmäßiger Sechsecke ist, dass sie eine Fläche lückenlos ausfüllen können (ebenso wie regelmäßige Dreiecke und Quadrate). Außerdem hat die regelmäßige 6-eckige Form den kleinsten Umfang für die größte Fläche unter den flächenfüllenden Polygonen, was sie sehr effizient macht.

Ein faszinierendes Beispiel aus diesem Youtubevideo ist das der Seifenblasen. Wenn du eine Seifenblase mit Wasser, Seife und etwas von deinem eigenen Atem erzeugst, hat sie immer eine Kugel-Form. Das liegt daran, dass das Volumen einer Kugel bei einer bestimmten Oberfläche das größte aller Objekte ist.

Wenn wir die Blasen jedoch auf einer ebenen Fläche zusammenlegen, verliert die Kugel ihren Effizienzvorteil, da der Querschnitt einer Kugel einen 2D-Raum nicht vollständig abdecken kann. Die nächstbeste Form in Bezug auf das Verhältnis von Volumen zu Oberfläche ist auch die beste, um die Spannung zwischen den Blasen auszugleichen, die auf der Oberfläche der Blasen entsteht. Wir sprechen hier natürlich von unserem allmächtigen Sechseck.

Seifenblasen sind eine interessante Möglichkeit, die Vorteile eines Sechsecks gegenüber anderen Formen zu veranschaulichen, es ist aber nicht die einzige Möglichkeit. In der Natur gibt es, wie wir bereits erwähnt haben, eine Vielzahl von Beispielen für sechseckige Formationen, die meist auf Spannungen im Material zurückzuführen sind. Wir können leider nicht auf alle im Detail eingehen. Wir können jedoch ein paar Orte nennen, an denen du in der Natur regelmäßige sechseckige Muster finden kannst:

• Honigwaben,
• organische Verbindungen,
• Stapel von Blasen,
• Felsformationen (wie die von Giant’s Causeway),
• Augen von Insekten,
• ...