Diagonale Rechteck Rechner

Unser Rechner für die Diagonale eines Rechtecks ist ein umfangreiches Werkzeug, mit dem du schnell die Diagonale und andere Parameter eines Rechtecks bestimmen kannst. Hast du ein bestimmtes Rechteck-bezogenes Problem oder weißt du nicht, wie man die Diagonale eines Rechtecks findet? Versuche, ein paar Parameter in die Felder neben dem Text einzugeben, oder lies weiter und finde heraus, welche Formeln es für die Diagonale eines Rechtecks gibt.

In der folgenden Abbildung siehst du ein typisches Rechteck. Wir haben fünf grundlegende Größen markiert, die ein bestimmtes Rechteck beschreiben. Du kannst sie verwenden, um die Formel für die Diagonale eines Rechtecks abzuleiten. Diese sind:

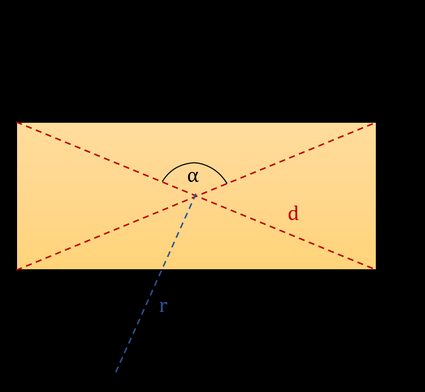
• a – die Länge,
• b – die Breite,
• α – der Winkel zwischen den Diagonalen,
• r – der Radius des Umkreises,
• d – die Diagonale;

und zwei weitere Parameter, die nicht auf dem Bild zu sehen sind:

• A – die Fläche und
• U – der Umfang.

Der Begriff Rechteck kommt vom lateinischen rectangulus, was eine Kombination aus zwei Wörtern ist: rectus (recht, richtig) und angulus (Winkel). Der Name leitet sich von der Tatsache ab, dass ein Rechteck ein Viereck mit vier rechten Winkeln ist (4 ∙ 90° = 360°). Seine gegenüberliegenden Seiten sind parallel und gleich lang, und seine beiden Diagonale schneiden sich in der Mitte und sind ebenfalls gleich lang.

Ein Quadrat ist ein besonderes Rechteck. Es ist folgendermaßen definiert: Seine vier Seiten sind gleich lang und seine zwei Diagonale bilden einen rechten Winkel. Probiere unsere Rechner aus, die sich mit Quadraten beschäftigen, z. B. den Quadrat Rechner 🇺🇸. Damit kannst du den Umfang, die Fläche und die Diagonale eines jeden Quadrats, schnell und einfach aus den Seitenlängen berechnen.

Der Mittelpunkt eines Rechtecks ist gleich weit von seinen Eckpunkten entfernt; deshalb kannst du immer einen Umkreis um ihn herum zeichnen. Andererseits kannst du einen Kreis nur dann in ein Rechteck** herein zeichnen (sodass er alle Seiten des Rechtecks berührt), wenn es ein Quadrat ist**.

Um die Diagonale eines Rechtecks zu bestimmen:

1. Schreibe die Seiten des Rechtecks auf – welche wir als a und b bezeichnen.
2. Nimm beide Werte hoch 2. Das heißt, du berechnest a² und b².
3. Addiere die beiden Werte aus Schritt 2 zusammen.
4. Ziehe die Quadratwurzel aus dem Ergebnis.
5. Das war's! Du hast gerade die Länge der Diagonale deines Rechtecks ermittelt.

Warum funktioniert dieses Verfahren?

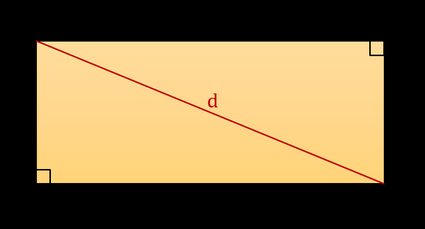
Um die oben verwendete Formel für die Diagonale eines Rechtecks herzuleiten, musst du ein Rechteck in zwei kongruente rechtwinklige Dreiecke teilen, d. h. in Dreiecke mit einem Winkel von 90°. Beide Dreiecke haben Seiten der Länge a und b und eine Hypotenuse der Länge d. Du kannst dann den Satz des Pythagoras anwenden, um die Diagonale eines Rechtecks zu bestimmen, die dann durch die folgende Formel ermittelt werden kann:

d² = a² + b²,

und jetzt weißt du bestimmt, wie du weiter vorgehen musst – berechne einfach die Quadratwurzel:

d = √(a² + b²).

Mit unserem Rechner für die Diagonale eines Rechtecks kannst du fast jede gewünschte Einheit verwenden. Schau dir unseren Längenumrechner oder Flächenumrechner an, um herauszufinden, wie du zwischen verschiedenen Einheiten (SI und den angloamerikanischen) wechseln kannst.

Manchmal ist die Länge zwei benachbarter Seiten eines Rechtecks nicht gegeben. Wie findet man in diesem Fall die Diagonale eines Rechtecks? Die Antwort findest du mit unserem Rechner für die Diagonale eines Rechtecks. Schreibe zunächst drei Grundgleichungen für den Flächeninhalt, den Umfang und den Radius des Umkreises auf:

1. Die Fläche eines Rechtecks: A = a ∙ b,
2. Der Umfang eines Rechtecks: U = 2 ∙ a + 2 ∙ b,
3. Der Umkreisradius eines Rechtecks: r = d/2.

Mit den obigen Gleichungen können wir nun verschiedene Formeln für die Diagonale eines Rechtecks ableiten, die von diesem Rechner für die Diagonale eines Rechtecks verwendet werden:

1. Länge und Breite sind gegeben:
   d = √(a² + b²);

2. Länge/Breite und Fläche sind gegeben:
   d = √(A²/a² + a²) oder d = √(A²/b² + b²);

3. Länge/Breite und Umfang sind gegeben:
   d = √(2a² - U ∙ a + U²/4)) oder d = √(2b² - U ∙ b + U²/4);

4. Länge/Breite und Winkel sind gegeben:
   d = b / sin(α/2) oder d = a / cos(α/2);

5. Fläche und Umfang sind gegeben:
   d = ½√(U² - 8 ∙ A);

6. Fläche und Winkel sind gegeben:
   d = √(2 ∙ A / sin(α));

7. Umfang und Winkel sind gegeben:
   d = U / (2 ∙ sin(α/2) + 2 ∙ cos(α/2));

8. Umkreisradius ist gegeben:
   d = 2 ∙ r.

Hinweis: **Der Winkel α zwischen den Diagonalen liegt gegenüber der Seite a**, wie in der ersten Abbildung dargestellt. Denke auch daran, dass der Rechner annimmt, dass die Länge größer ist als die Breite.

Wusstest du, dass es ein besonderes Rechteck gibt, das sogenannte Goldene Rechteck? Wenn nicht, dann schau dir unseren Goldenes Rechteck Rechner an, um zu erfahren, wie du Goldene Rechtecke konstruieren kannst!