Flächeninhalt eines Quaders Rechner

Willkommen beim Rechner für den Flächeninhalt eines Quaders oder rechteckigen Prismas. Hier hast du die Möglichkeit, schnell und einfach alles über deinen Quader zu erfahren! Wir erklären dir vor allem, wie du seine Oberfläche berechnen kannst. Möchtest du deine Scheune streichen und fragst dich wie viel Farbe du brauchst 🇺🇸? Oder baust du einen Pool in deinem Garten und möchtest wissen, wie viele Fliesen du verlegen musst?

Egal, wie die Frage lautet, solange sie auf „Wie groß ist die Oberfläche eines Quaders” hinausläuft, bist du hier genau richtig!

Bevor wir sehen, wie groß die Oberfläche eines Quaders ist, sollten wir uns mit dieser Form vertraut machen.

Stell dir einen normalen Karton vor, das ist ein rechteckiges Prisma bzw. ein Quader! Oder erinnerst du dich an die Zeichnungen von Häusern, die wir im Kindergarten gemacht haben? Wenn du das eckige Dach entfernst, hast du ein weiteres Beispiel für ein rechteckiges Prisma.

Formal (mathematisch) gesehen ist ein Quader oder rechteckiges Prisma ein Körper, bei dem alle sechs Seiten Rechtecke sind, die senkrecht zueinander stehen. Das bedeutet, dass es drei Paare von identischen Flächen gibt, die auf den gegenüberliegenden Seiten des Körpers liegen.

Die untere und obere Seite des Quaders werden Grundflächen genannt, und jede der anderen vier Flächen wird Seitenfläche genannt. Die Seitenlängen eines jeden Rechtecks werden Kanten genannt (wiederum unterteilt in Basiskanten und Seitenkanten).

Nach der Klärung der Terminologie ist es Zeit, sich auf die Berechnung des Flächeninhalts für Quader zu konzentrieren.

Um herauszufinden, wie groß die Oberfläche eines Quaders oder rechteckigen Prismas ist, müssen wir die Werte aller drei Seiten kennen. Beginnen wir mit der Schreibweise, die wir für sie und für die anderen Werte in unserem Rechner verwenden:

• l – ist die Länge der ersten Basiskante,
• b – ist die Länge der zweiten Basiskante,
• h – ist die seitliche Kantenlänge bzw. Höhe,
• A_b – ist die Grundfläche des Quaders,
• A_l – ist die Seitenfläche des Quaders,
• A – ist die Oberfläche des Quaders, und
• V – ist das Volumen des Quaders.

Beachte, dass A_b die Oberfläche einer einzigen Grundfläche unseres Prismas bezeichnet. A_l hingegen bezeichnet die Gesamtfläche der vier Seitenflächen. Da der Körper zwei Grundflächen hat (die untere und die obere), lautet die Formel für den Flächeninhalt eines Quaders wie folgt:

Oberflächeninhalt = 2 ∙ Grundfläche + Seitenfläche,

bzw.

A = 2 ∙ A_b + A_l.

Erinnere dich daran, dass alle unsere Flächen Rechtecke sind, welche durch die Multiplikation der Seitenlängen berechnet werden. Nutzen wir diese Informationen, um die Grundfläche unseres Quaders zu untersuchen. Die Fläche eines Rechtecks mit den Seitenlängen l und b ist also A = l ∙ b. Das ist auch genau die Formel für die Grundfläche:

A_b = l ∙ b.

Ein Kinderspiel, nicht wahr? Versuchen wir es jetzt mit etwas Komplizierterem und gehen zur Seitenfläche über. Wir haben vier Flächen, die zu diesem Wert beitragen, alles Rechtecke. Außerdem sind von den vier Flächen je zwei identisch (die Vorder- und Rückseite und die linke und rechte Seite). Bei allen ist eine Seite gleich h, die Höhe des Quaders. Eine andere Seite eines der Paare ist gleich die erste Basiskante l, und die andere ist gleich der Länge der zweiten Basiskante b. Alles in allem erhalten wir, dass die Seitenfläche A_l gleich:

A_l = l ∙ h + l ∙ h + b ∙ h + b ∙ h,

oder einfach

A_l = 2 ∙ l ∙ h + 2 ∙ b ∙ h ist.

Zusammen mit der Grundfläche können wir so die Formel für die Oberfläche eines Quaders herleiten:

A = 2 ∙ A_b + A_l = 2 ∙ l ∙ b + 2 ∙ l ∙ h + 2 ∙ b ∙ h.

Nehmen wir an, du möchtest einen Swimmingpool fliesen und möchtest dafür wissen, wie groß die Fläche ist, die du fliesen musst. Wenn der Pool rechteckig ist und einen flachen Boden hat, dann haben wir es genau mit einem Quader bzw. rechteckigen Prisma zu tun! Schauen wir uns eine Abbildung zur Visualisierung an:

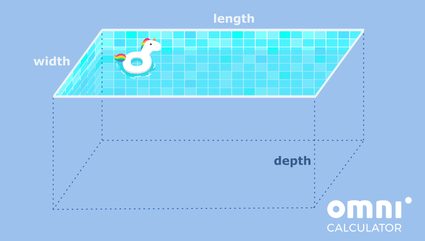
Okay, wir wissen, dass es schwer ist, die Augen von der Einhorn-Luftmatratze abzuwenden, aber lass uns zum eigentlichen Problem zurückkehren!

Nehmen wir an, dass der Pool eine Länge von 8 Metern, eine Breite von 6 Metern und eine Tiefe von 2 Metern hat. Setzten wir die Werte in die obige Gleichung ein:

Die Seiten der Grundfläche unseres Pools sind seine Länge und seine Breite, die in unserem Fall l = 8 m und b = 6 m betragen. Es ist ganz egal, in welcher Reihenfolge wir die Zahlen einsetzen; denn das bedeutet nur, dass wir das Becken aus einem anderen Winkel betrachten und ändert nichts an seiner Oberfläche.

Es bleibt die Tiefe unseres Beckens und der Wert für h im Rechner übrig: setze h = 2 m für die Tiefe bzw. Höhe des Beckens ein.

Der Rechner für den Flächeninhalt eines Quaders gibt uns die Lösung:

A = 2 ∙ l ∙ b + 2 ∙ l ∙ h + 2 ∙ b ∙ h = 2 ∙ 8 m ∙ 6 m + 2 ∙ 8 m ∙ 2 m + 2 ∙ 6 m ∙ 2 m = 152 m².

Aber das ist die Fläche des gesamten Quaders, wir möchten den Pool schließlich nicht zum Überfließen 🇺🇸 bringen.

Um die richtige Antwort zu finden, lass uns in den Erweiterten Modus des Rechners wechseln. Er ermöglicht es uns, die Grundfläche und die Seitenfläche der Form zu sehen. Da wir wissen, wie man die Grundfläche eines rechteckigen Prismas ermittelt, wissen wir, dass:

A = 2 ∙ A_b + A_l ist.

Wir müssen nur die Fläche, die wir nicht mit Wasser füllen (also die Oberseite), davon abziehen. Da die obere Fläche gleich der Unteren ist, ist die Fläche, die wir fließen müssen:

Fläche = A - A_b,

was in unserem Fall bedeutet:

Grundfläche = 152 m² - 48 m² = 104 m².

Damit sind wir einen Schritt näher an der Fertigstellung des Pools und können dein Werk bei einem kühlen Getränk bewundern. Der Quader ist aber nicht die einzige dreidimensionale Form mit rechteckiger Grundfläche; mehr dazu erfährst du im Flächeninhalt einer rechteckigen Pyramide Rechner 🇺🇸.