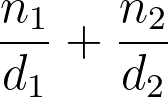Bruchrechner

Willkommen bei unserem Bruchrechner, einem wirklich vielseitigen Werkzeug. Es kann zwei beliebige Brüche:

• ➕ addieren,
• ➖ subtrahieren,
• ✖️ multiplizieren und
• ➗ dividieren.

Außerdem kannst du hier Brüche kürzen (vereinfachen) und einen Bruch in eine Dezimalzahl umwandeln und umgekehrt. Wenn du immer noch nicht beeindruckt bist, bedenke, dass dieses Tool nicht nur mit regulären echten und unechten Brüchen umgehen kann, sondern auch mit gemischten Zahlen – was könnte man sich mehr wünschen? 😁

Wir haben eine einführende Lektüre vorbereitet, die dich in die Welt der Brüche eintauchen lässt 🌎. Im Folgenden erfährst du, wie Brüche definiert werden, welche Arten von Brüchen es gibt (echte, unechte, gemischte Zahlen) und welche Grundoperationen mit Brüchen und gemischten Zahlen möglich sind. Bist du bereit?

Ein Bruch ist die Anzahl der gleichen Teile eines Ganzen.
Du erkennst einen einfachen Bruch daran, dass er zwei Zahlen enthält, die durch einen Strich (oder Schrägstrich) voneinander getrennt sind:

• Die obere Zahl nennen wir den Zähler und schreiben sie über den Strich. Sie sagt uns:

  Wie viele Teile wir haben.

• Die untere Zahl ist der Nenner und wir schreiben ihn unter den Strich. Er steht für:

  Die Gesamtzahl der Teile.

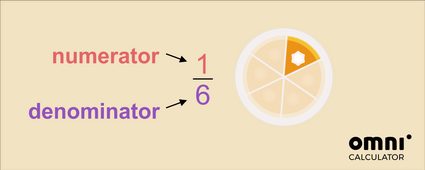
Im obigen Beispiel bedeutet der Bruch 1 Teil von 6 Stücken, in die der Kuchen insgesamt geschnitten wurde. Es ist also ein Sechstel der ganzen Torte.

Aber natürlich kann der Kuchen auch ganz anders geschnitten werden!

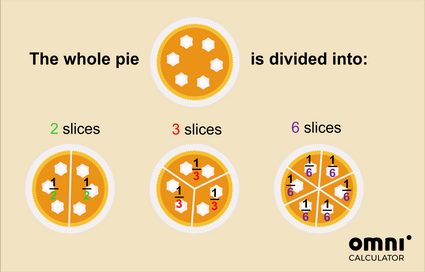
Wenn du die Torte also in 2 Teile schneidest, dann ist ein Stück die Hälfte der ganzen Torte. Wenn du die Torte in 3 Teile schneidest, dann ist ein Stück ein Drittel der ganzen Torte usw.

Brüche werden überall um uns herum verwendet:

• Jedes Mal, wenn du einen Teil eines Ganzen ausdrücken möchtest, das in gleichmäßige Stücke geteilt werden kann: wie ein Kuchen 🍰, ein Schokoriegel 🍫, eine Wassermelone 🍉, eine Pizza 🍕, usw.;

• Wenn wir etwas in imperialen Einheiten messen 📏, besonders in Zoll oder Achtel Zoll, und

• Die Größe deines Computerbildschirms 🖥️ wird als Verhältnis ausgedrückt, z. B. 16:9 – das ist auch ein Bruch, nur anders geschrieben. (Wie du Verhältnisse kürzen kannst, erfährst du in unserem Quotientenrechner 🇺🇸)!

Nachdem du nun die Definition von Brüchen kennst, lass uns die 3 allgemeinen Arten von Brüchen ansehen – echte, unechte Brüche und gemischte Zahlen:

1. Echte Brüche

   Bei echten Brüchen ist die oberste Zahl (Zähler) kleiner als die unterste Zahl (Nenner). Das bedeutet, dass der Wert des Bruchs immer kleiner ist als eine ganze Zahl, z. B.:

   🍰 5 Kuchenstücke von einem Kuchen, der in 6 Stücke geschnitten wurde,

   🍫 2 Reihen einer Schokoladentafel, die insgesamt 5 Reihen hat, oder

   🍊 7 Stücke einer ganzen Orange, die wir in 8 Stücke geschnitten haben.

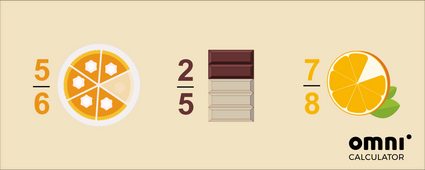
Die allgemeine Regel, die sowohl für positive als auch für negative Zahlen gilt, ist, dass der absolute Wert des Bruches kleiner als eins ist:

|^Zähler/_Nenner| < 1

2. Unechte Brüche

   Was ist dann ein unechter Bruch? Das ist ein Bruch, bei dem der Zähler größer als (oder gleich) der Nenner ist. Beispiele für unechte Brüche sind:

   🍰 10 Stücke von 2 Kuchen, wenn jeder Kuchen 6 Stücke hat;

   🍫 8 Reihen von 2 Schokoriegeln, wenn jeder ganze Schokoriegel 5 Reihen hat; oder

   🍊 21 Teile einer Orange, wenn wir jede Orange in 8 gleiche Stücke schneiden.

3. Gemischte Zahlen

   Gemischte Zahlen drücken einen unechten Bruch anders aus. Sie setzen sich aus ganzen Zahlen (die Anzahl der Ganzen) und einem echten Bruch zusammen. Schauen wir uns also die Beispiele aus dem vorherigen Abschnitt an:

   🍰 10 Stücke Kuchen, wenn jeder Kuchen 6 Stücke hat, ist das gleiche wie → 1 ganzer Kuchen und 4 Stücke von 6;

   🍫 8 Reihen Schokolade, wenn jede ganze Tafel Schokolade 5 Reihen hat → 1 ganze Tafel Schokolade und 3 Reihen von 5; oder

   🍊 21 Teile einer Orange, wenn wir die Orange in 8 Scheiben schneiden → 2 ganze Orangen und fünf Scheiben von 8.

Für die Addition von Brüchen gibt es drei Szenarien:

1. Der Nenner (die untere Zahl) ist in beiden Brüchen gleich – z. B. ³/₅ and ¹/₅

   Dies ist der einfachste Fall – du musst nur die Zähler (oberen Zahlen) addieren und den Nenner unverändert lassen, z. B.:

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅

2. Die Brüche haben ungleiche Nenner – z. B. ²/₅ und ³/₁₀

   Das ist ein etwas komplizierterer Fall – um diese Brüche zu addieren, musst du einen gemeinsamen Nenner finden.

   • Du kannst z. B. kgV – das kleinste gemeinsame Vielfache – verwenden, um die gemeinsame Zahl deiner beiden Nenner zu finden: kgV(5,10) = 10. Eine andere Möglichkeit ist, die Nenner zu multiplizieren und den Bruch später zu kürzen.

   • Dann musst du jeden Bruch so erweitern, dass er diesen gemeinsamen Nenner als Grundzahl hat:

   Du solltest also den Bruch mit dem Nenner gleich 5 (unser 1/5) mit 2 multiplizieren, um 10 zu erhalten (denke daran, dass du sowohl die obere als auch die untere Zahl multiplizieren musst):

   ➽ ²/₅ = ^{(2 × 2)}/_{(5 × 2)} = ⁴/₁₀

   Bei deinem zweiten Bruch ist der Nenner bereits 10:

   ➽ ³/₁₀

   • Jetzt, wo deine Brüche denselben Nenner haben, kannst du sie addieren:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀

3. Du möchtest zwei gemischte Zahlen addieren – z. B. 2 ³/₅ und 1 ¹/₂

   Um dieses Problem zu lösen, kann man den gemischten Bruch in einen unechten Bruch umwandeln und dann wie gewohnt addieren.

   Konvertieren wir 2 ³/₅

   • Multipliziere die ganze Zahl mit dem Nenner:

     2 ∙ 5 = 10

   • Addiere das Ergebnis zu deinem Zähler:

     10 + 3 = 13

   • Das ist dein neuer Zähler – schreibe ihn über deinen Nenner:

     2 ³/₅ = ¹³/₅

   Analog dazu kannst du auch 1 ¹/₂ = ³/₂ herausfinden.

   • Führe die Standardaddition von Brüchen mit ungeraden Nennern durch:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀

   • Schließlich kannst du dein Ergebnis wieder in einen gemischten Bruch umwandeln:

     Führe eine schriftliche Division mit einem Rest durch:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀

Natürlich kommt unser Bruchrechner mit all diesen Szenarien klar. 😎

Wenn du dich immer noch fragst, wie das Addieren von Brüchen funktioniert, hilft dir vielleicht diese Grafik:

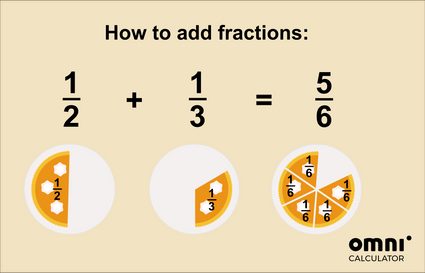
Eine noch ausführlichere Erklärung findest du in unserem Brüche Addieren Rechner 🇺🇸.

Wenn du dich fragst, wie man Brüche subtrahiert, und du den vorherigen Abschnitt Rechenregeln zum Addieren von Brüchen gelesen hast, haben wir eine gute Nachricht für dich: Es ist so ziemlich dasselbe!

1. Wenn zwei Brüche denselben Nenner haben, subtrahiere die Zähler:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅

2. Beim Subtrahieren von Brüchen mit ungleichen Nennern – ²/₅ und ³/₁₀ – wiederholst du das Verfahren aus dem vorherigen Abschnitt, wobei du im letzten Schritt subtrahierst und nicht addierst:

   • Finde einen gemeinsamen Nenner – in diesem Fall also 10.

   • Erweitere die Brüche zu ihren gleichwertigen Brüchen mit einem gemeinsamen Nenner: ⁴/₁₀ und ³/₁₀.

   • Subtrahiere die Zähler.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀

3. Für gemischte Zahlen (2³/₅ und 1 ¹/₂):

   • Ändere die gemischten Zahlen in unechte Brüche um, so wie zuvor:

     2 ³/₅ = ¹³/₅ und 1 ¹/₂ = ³/₂

   • Subtrahiere die beiden unechten Brüche mit ungleichen Nennern:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀

   • Belasse es bei einem unechten Bruch oder wandle ihn wieder in eine gemischte Zahl um:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀

Du kannst dir die Subtraktion so vorstellen, dass du einen Teil des Kuchens nimmst oder isst:

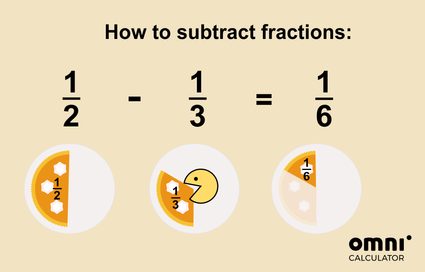
Das war doch gar nicht so schwer, oder?

Das Multiplizieren von Brüchen ist – glücklicherweise – eine mühelose Operation. Es ist einfach Zähler mal Zähler über Nenner mal Nenner. Manchmal musst du den Bruch auch kürzen. Und das war's!

Sieh dir dieses Beispiel an:

➽ ²/₃ ∙ ⁵/₆ = ^{(2 ∙ 5)}/_{(3 ∙ 6)} = ¹⁰/₁₈,

was du dann zu ⁵/₉ kürzen kannst.

Wann immer du mit gemischten Zahlen zu tun hast, vergiss nicht, dass du sie vor der Multiplikation immer als unechte Zahl schreiben musst:

➽ 2 ¹/₂ ∙ 3 ¹/₄ = ⁵/₂ ∙ ¹³/₄ = ^{(5 ∙ 13)}/_{(2 ∙ 4)} = ⁶⁵/₈ = 8 ¹/₈

Und wenn du einen Bruch mit einer ganzen Zahl multiplizierst, denk daran, dass du die ganze Zahl als sich selbst geteilt durch 1 schreiben kannst:

➽ 3 ∙ ⁵/₇ = ³/₁ ∙ ⁵/₇ = ^{(3 ∙ 5)}/_{(1 ∙ 7)} = ¹⁵/₇

Wenn du nicht weißt, wie du mit dem Kürzen von Brüchen umgehen sollst, scrolle nach unten zum Abschnitt Wie kürzt man Brüche?.

Da du nun weißt, wie du Brüche multiplizierst, kommen wir zum letzten Thema, der Division von Brüchen.

Zerbrichst du dir den Kopf darüber, wie man Brüche teilt? Mach dir keine Sorgen! Die Division von Brüchen ist der Multiplikation von Brüchen sehr ähnlich. Der einzige Unterschied besteht darin, dass du deine erste Zahl mit dem Kehrwert des zweiten Bruches multiplizieren musst. Das mag etwas seltsam klingen, aber es ist in Wirklichkeit ganz einfach! Sieh dir dieses Beispiel an:

(¹/₂) / (³/₅) = ¹/₂ ∙ ⁵/₃ = ^{(1 ∙ 5)}/_{(2 ∙ 3)} = ⁵/₆

Du musst also nur den zweiten Bruch umdrehen (seinen Kehrwert bilden) und die Brüche multiplizieren. Manchmal musst du die Brüche noch kürzen. Das ist alles, tadaaa! 🎉

Wir möchten uns unser Leben natürlich so einfach wie möglich machen — vor allem in der Mathematik. Deshalb ist es so wichtig, Brüche zu kürzen. Es bedeutet, dass wir den Bruch in seiner einfachsten Form schreiben.

Aber was bedeutet das genau? Sieh dir diese Beispiele an:

• Du würdest lieber sagen, dass ein Viertel der Pizza übrig ist, anstatt zwei Achtel, oder?
• Die Hälfte eines Kuchens wurde gegessen, nicht drei Sechstel.

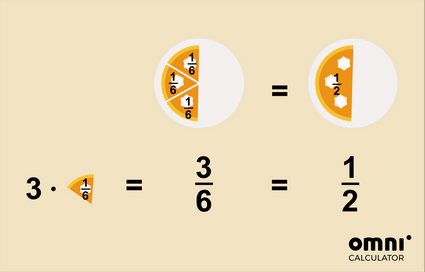
Um einen Bruch zu vereinfachen, kannst du zwei Methoden verwenden:

1. Teile den Bruch durch 2, 3, 5, 7, 11 ... bis es unmöglich ist, die Division (ohne einen Rest) fortzusetzen:

   ➽ ⁴²/₁₂₆ = | :2

   ➽ ²¹/₆₃ = | :3

   ➽ ⁷/₂₁ = | :7

   ➽ ¹/₃

2. Finde den ggT — größten gemeinsamen Teiler — von Zähler und Nenner und teile sie dann durch diese Zahl: ggT(42,126) = 42, also

   ➽ ⁴²/₁₂₆ = | :42

   ➽ ¹/₃

Mehr über das Vereinfachen von Brüchen erfährst du in unserem speziellen Brüche Kürzen Rechner 🇺🇸. Wirf auch einen Blick auf unseren erstaunlichen Gleichwertige Brüche Rechner 🇺🇸, der viele Äquivalente zu deinem Bruch finden kann.

Wenn du herausfinden möchtest, wie man eine Dezimalzahl in einen Bruch umwandelt, bist du hier genau richtig. Sieh dir diese Schritt-für-Schritt-Anleitung an:

Nehmen wir an, du möchtest 0,32 in einen Bruch umwandeln:

1. Betrachte deine Dezimalzahl als Zähler. Dann wird der Nenner 1 sein.

2. Verschiebe das Komma nach rechts, bis du nur noch eine ganze Zahl hast:

   0,32 → 3,2 → 32

   Jeder Schritt entspricht einer Multiplikation mit 10:

   0,32 ∙ 10 → 3,2 ∙ 10 → 32

3. Du hast den Zähler mit 10 ∙ 10 multipliziert, jetzt müssen wir den Nenner mit der gleichen Zahl multiplizieren:

   1 ∙ 10 ∙ 10 = 100

4. Du hast deinen Bruch in eine Dezimalzahl umgewandelt! ✨ 0,32 → ³²/₁₀₀

5. Schließlich kürzt du das Ergebnis. Da der größte gemeinsame Teiler für 32 und 100 4 ist, teile sowohl den Zähler als auch den Nenner durch diesen Wert:

   ➽ ³²/₁₀₀ = ⁸/₂₅

Und das war's, schon haben wir den Bruch in seiner einfachsten Form. ❤️

Der einfachste Weg, einen Bruch in eine Dezimalzahl umzuwandeln, ist ... einen Taschenrechner zu verwenden. Sei es dieser Bruchrechner, ein normaler Taschenrechner oder unser spezielles Tool — Bruchzahl zu Dezimalzahl Umrechner 🇺🇸.

Manchmal ist es relativ einfach, einen Bruch ohne Hilfsmittel in eine Dezimalzahl umzuwandeln — wie 1/2, 3/4 (oder sogar 1/8). Du wirst wahrscheinlich kein Problem damit haben, die oben genannten Brüche so zu erweitern, dass 10, 100, 1000 usw. im Nenner steht:

• Multipliziere ¹/₂ mit 5, um 10 als Nenner zu erhalten:

  ➽ ¹/₂ = ⁵/₁₀ = 0,5

• Multipliziere ³/₄ mit 25, um 100 als Nenner zu erhalten:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0,75

• Multipliziere ¹/₈ mit 125, um 1000 als Nenner zu erhalten:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0,125

Aber was ist, wenn du weder Internet noch einen Taschenrechner hast, sondern nur Stift und Papier📝? Und dein Bruch sieht nicht so einfach zu erweitern aus wie die oben genannten? Dann musst du die schriftliche Division bis zu den Nachkommastellen wahrscheinlich schriftlich durchführen. Viel Glück! 🤞

Zunächst musst du einen gemeinsamen Nenner finden. Addieren wir beispielsweise 1/2 und 3/5. Befolge diese Schritte, um Brüche mit unterschiedlichen Nennern zu addieren:

1. Bestimme das kleinste gemeinsame Vielfache (kgV) des Nenners:

   • 10

2. Dividiere das kgV durch jeden Nenner und multipliziere die Zähler mit dem Ergebnis:

   • 10/2 = 5
     5 ∙ 1 = 5

   • 10/5 = 2
     2 ∙ 3 = 6

3. Addiere die in Schritt 2 berechneten Zahlen und setzte die Antwort über das kgV:

   • 6 + 5 = 11

   • 11/10 = 1 ¹/₁₀

4. Voila! Du hast beide Brüche addiert.

Ja, jeder Bruch ist eine rationale Zahl, aber nicht alle rationale Zahlen sind Brüche. Eine rationale Zahl ist nur dann ein Bruch, wenn der Zähler und der Nenner ganze Zahlen sind.

0,3333 als Bruch geschrieben ist ³³³³/₁₀₀₀₀.

Um diese Antwort zu finden:

1. Schreibe die Dezimalzahl in den Zähler und 1 in den Nenner:

   0,3333/1

2. Verschiebe das Komma am Ende der Zahl nach rechts, damit sie als ganze Zahl erscheint:

   3333

3. Füge die gleiche Anzahl von Nullen zum Nenner hinzu wie die Anzahl der Stellen, um die du das Komma verschoben hast. In diesem Fall sind es vier:

   10000

4. Setze die Zahl aus Schritt 2 in den Zähler und die Zahl aus Schritt 3 in den Nenner ein:

   3333/10000

Das Produkt aus 1/2 und 5/3 ist 5/6.

Um diese Antwort zu erhalten, müssen wir Zähler und Nenner folgendermaßen multiplizieren:

• 1 ∙ 5 = 5 und

• 2 ∙ 3 ist 6, also:

• 1/2 ∙ 5/3 = 5/6.