Binomialkoeffizient Rechner

Willkommen beim Binomialkoeffizient Rechner, mit dem du alles mithilfe der geheimnisvollen Formel „n über k“ berechnen und mehr darüber erfahren kannst. Der Ausdruck bezeichnet die Anzahl der Kombinationen von k Elementen aus einer Gruppe mit n Elementen und entspricht der nCr-Taste auf einem echten Taschenrechner.

Im folgenden Text findest du Antworten auf die Fragen:

• „Was ist ein Binom?“;
• „Wie wird der Binomialkoeffizient berechnet?“;
• Welche Bedeutung hat die Kombination?;
• Was ist die Lösung von „5 über 3“ oder „4 über 2“?; und
• Wie unterscheiden sich Permutation und Kombination voneinander?

In der Mathematik (genauer gesagt in der Algebra) ist ein Binom ein Polynom mit zwei Termen (daher die Vorsilbe „bi-”). Die Ausdrücke x + 1, xy - 2ab oder x³z - 0,5y⁵ sind beispielsweise alle Binome, aber x⁵, a + b - cd oder x² - 4x² sind es nicht (der letzte Ausdruck hat zwar zwei Terme, aber wir können ihn zu den einfachen Term -3x² vereinfachen).

Da wir nun wissen, was ein Binom ist, schauen wir uns den Exponenten genauer an:

(x² - 3)³.

Es gibt einige Spezialfälle dieses Ausdrucks – die kurzen Multiplikationsformeln, die du vielleicht aus der Schule kennst:

(a + b)² = a² + 2ab + b²,

(a - b)² = a² - 2ab + b².

Das Polynom, das wir auf der rechten Seite erhalten, ist die quadratische Ergänzung dessen, was in den Klammern stand. Ob du es glaubst oder nicht, wir können ihre Formeln für jede positive ganzzahlige Potenz finden. Der binomische Lehrsatz sagt uns ganz allgemein, wie diese Erweiterung aussieht:

wobei:

• $C_k$ die Anzahl aller möglichen Kombinationen von $k$ Elementen aus einer Gruppe mit $n$ Elementen ist.

Für ein bestimmtes n werden diese Zahlen für aufeinanderfolgende Werte von n in den Zeilen des sogenannten Pascalschen Dreiecks übersichtlich dargestellt. Dabei ergibt jede einzelne Zeile als Ganzes alle möglichen Teilmengen der Gruppe (d. h. die Kardinalität der Potenzmenge) zählt. Besuche unseren Pascalsches Dreieck Rechner, um das Pascalsche Dreieck in der von dir gewählten Größe zu berechnen.

Das ist ein guter Moment, um uns die Bedeutung von „Kombination“ anzuschauen – da wir sie schon so oft erwähnt haben.

Um besser zu verstehen, wie man den Binomialkoeffizienten berechnet, schauen wir uns ein Beispiel an: Stell dir vor, du bist als Student in einer Vorlesung und machst ein Nickerchen. Plötzlich reißt dich der Lehrer aus deinem Schlummer, indem er verkündet: „Die Gruppen für die Zwischenprüfungen werden nun zufällig ausgewählt.“ Es scheint, als ob noch etwas Arbeit auf dich zukommt.

Das Problem ist, dass es nur eine Person gibt, mit der du an dem Projekt zusammenarbeiten möchtest. Wenn es zwanzig Leute in der Gruppe gibt und der Lehrer euch in zufällige Vierergruppen einteilt, wie groß ist dann die Wahrscheinlichkeit, dass du mit deinem Freund zusammenarbeiten wirst?

Jede mögliche Gruppenkonstellation ist ein Beispiel für eine Kombination. In diesem Fall eine Kombination von vier Elementen (k) aus einer Gruppe mit zwanzig Elementen (n) oder von vier Schülern aus einer Gruppe mit zwanzig Personen. Wenn du es genau wissen möchtest, bedeutet die Wahl einer Kombination, dass du eine Teilmenge aus einer größeren Menge auswählst. Das Wichtigste dabei ist, dass die Reihenfolge der Elemente, die wir auswählen, keine Rolle spielt. Schließlich sind alle Mitglieder eines Projektteams gleichberechtigt (außer vielleicht denen, die keine Arbeit leisten).

Die Anzahl der Kombinationen von k Elementen aus einer Menge von n Elementen wird geschrieben als:

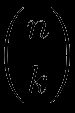
Wie bei einem Bruch, n geteilt durch k, aber ohne den Bruchstrich dazwischen, was wir als „n über k“ lesen. Das ist auch das Symbol, das erscheint, wenn wir nCr auf einem Taschenrechner drücken (nicht auf unserem Binomialkoeffizient Rechner, sondern auf einem normalen, realen Rechner). Ein Beispiel um den Binomialkoeffizienten zu berechnen:

ist „4 über 2” und

ist „6 über 2”. In manchen Lehrbüchern wird der Binomialkoeffizient auch mit C(n,k) bezeichnet, was ihn zu einer Funktion von n und k macht. Schauen wir uns an, wie du Terme wir „5 über 3” mit dem Binomialkoeffizienten Rechner lösen kannst – es ist ganz einfach. Die Formel um n über k zu berechnen lautet:

n! / (k! · (n - k)!).

Das Ausrufezeichen wird als Fakultät bezeichnet. Der Ausdruck n! ist das Produkt der ersten n natürlichen Zahlen, d. h.,

n! = 1 · 2 · 3 · ... · n.

Das Beispiel 4 über 2 von oben wäre also:

4! / (2! · (4 - 2)!) = (1 · 2 · 3 · 4) / (1 · 2 · 1 · 2) = 6,

und 6 über 2 ist

6! / (2! · (6 - 2)!) = (1 · 2 · 3 · 4 · 5 · 6) / (1 · 2 · 1 · 2 · 3 · 4) = 15.

Wenn du mehr über die Fakultät wissen möchtest, besuche unseren Fakultät Rechner 🇺🇸!

Wir können zwei Elemente aus einer Menge von vier auf sechs verschiedene Arten auswählen und aus einer Menge von sechs auf fünfzehn verschiedene Arten.

Bevor wir weitermachen, schauen wir uns noch einmal die Formel des n über k Rechners an, um n über k zu berechnen. Wir können daraus eine recht interessante, symmetrische Eigenschaft ableiten.

Wenn wir n über n - k wählen, dann erhalten wir

n! / ((n - k)! · (n - (n - k))!) = n! / ((n - k)! · k!)

was dasselbe ist wie n über k, da die Multiplikation kommutativ ist. Mit anderen Worten:

oder C(n,k) = C(n,n-k).

Im obigen Abschnitt des Binomialkoeffizient Rechners haben wir gesehen, was die Fakultät ist. In der Kombinatorik bezeichnet dies die Anzahl der Permutationen. Eine Permutation der Länge n bedeutet, n Elemente in eine bestimmte Reihenfolge zu bringen. Wenn wir zum Beispiel drei süße Kätzchenausdrücke haben, sagen wir 😹, 😻 und 🙀, dann können wir sie auf sechs verschiedene Arten in einer Reihenfolge anordnen:

(😹, 😻, 🙀),

(😹, 🙀, 😻),

(😻, 😹, 🙀),

(😻, 🙀, 😹),

(🙀, 😹, 😻), oder

(🙀, 😻, 😹).

Beachte, dass dies mit dem Ergebnis der Fakultät übereinstimmt:

3! = 3 · 2 · 1 = 6.

Mit unserem Permutationsrechner 🇺🇸 kannst du noch tiefer in dieses Thema eintauchen.

Beachte, dass wir diese Formel auch so verstehen können: Wir wählen das erste Element aus drei (3 Möglichkeiten), das zweite aus den zwei verbleibenden (weil wir bereits eine gewählt haben – somit verbleiben 2 Möglichkeiten) und das dritte aus dem verbleibenden (weil wir bereits zwei Möglichkeiten gewählt haben - 1 verbleibt). Wir multiplizieren die Anzahl der Wahlmöglichkeiten: 3 · 2 · 1 = 6, und erhalten so die Fakultät.

Wenn wir die Permutation mit der Kombination vergleichen, ist das Schlüsselwort die Reihenfolge. Wie wir bereits im vorigen Abschnitt festgestellt haben, besteht die Bedeutung hinter einer Kombination darin, einige Elemente aus einer größeren Sammlung auszuwählen. Im Grunde genommen sagen wir, welche Elemente wir auswählen, aber nicht, welches das erste, zweite usw. ist, die Auswahl ist also zufällig. Sie bilden eine Gruppe als Ganzes.

Bei einer Permutation hingegen werden die Elemente in einer festen Reihenfolge hintereinander angeordnet, sodass es sich um eine Abfolge und nicht um eine gruppe handelt. Außerdem werden bei einer Permutation alle Elemente aus der Menge verwendet, während bei einer Kombination nur einige von ihnen ausgewählt werden.

Versetze dich beispielshalber noch einmal in die Lage eines Schülers. Als die Lehrkraft deine Gruppe für dich auswählte, wählte sie eine Kombination. Und wenn es dann an der Zeit ist, dein Projekt zu präsentieren und sie jedem von euch eine Frage stellt, wählt sie eine Permutation (die Lehrkraft bestimmt die Reihenfolge, in der sie euch die Fragen stellt). Und wir alle wissen, wie wichtig diese Reihenfolge für deine Endnote sein kann!

Binomialkoeffizienten sind eine der wichtigsten Abfolgen in der diskreten Mathematik und Kombinatorik. Sie tauchen sehr häufig in Statistik- und Wahrscheinlichkeitsberechnungen auf und sind in der Binomialverteilung (einschließlich der negativen Binomialverteilung 🇺🇸) vermutlich von größter Bedeutung. Bedeutet das, dass nur Mathematik-Freaks wirklich etwas damit anfangen können?

Jedes Glücksspiel beruht auf dem Zufall, und die Binomialkoeffizienten spielen dabei eine entscheidende Rolle. Ein einfacher Münzwurf ist das beste Beispiel, das du mit unserem Münzwurf Wahrscheinlichkeit Rechner berechnen kannst. Gehen wir aber noch einen Schritt weiter und schauen uns das Pokern mit dem n über k Rechner an.

Hast du dich schon einmal gefragt, warum manche Blätter beim Poker wertvoller sind als andere? Das liegt ganz einfach daran, dass sie seltener sind (es sei denn, jemand betrügt, aber wir haben genug Gangster-Fernsehserien gesehen, um zu wissen, dass dies üblicherweise eine schlechte Idee ist).

Ein normales Kartenspiel besteht aus 52 Karten, und beim Texas Hold'em erhält jeder Spieler fünf Karten. Unser Binomialkoeffizient Rechner und die n über k-Formel (in unserem Fall mit n = 52 und k = 5) sagen uns, dass dies zu 2 598 960 möglichen Händen in einem Pokerspiel führt. Ganz schön viel, findest du nicht? Und nun betrachte das bestmögliche Blatt — einen Royal Flush in Kreuz (Ass, König, Dame, Bube und 10). Dieses Blatt kann nur in einem Fall vorkommen —wenn wir genau diese Karten bekommen. Das bedeutet, dass die Wahrscheinlichkeit, dieses Blatt zu bekommen, 1 zu 2 598 960 beträgt – überprüfe das Ergebnis mit dem Binomialkoeffizienten Rechner! Wir raten dir davon ab, deine gesamten Ersparnisse auf diese Chance zu setzen.

Nehmen wir ein anderes Beispiel um den Binomialkoeffizienten zu berechnen — ein Full House (Drilling und ein Paar). Diesmal gibt es wesentlich mehr Möglichkeiten. Schließlich kann jede der 13 Karten einer Farbe ein Dreier sein und das Paar befindet sich in einer der anderen 12 Karten (es kann nicht den gleichen Wert wie der Dreier haben). Außerdem kommt der Drilling nur in drei der vier Kartensymbole vor und das Paar nur in zwei.

Erinnern wir uns an die Bedeutung einer Kombination! Wir müssen drei von vier Symbolen für den Drilling und eine Kombination von zwei von vier für das Paar wählen. Der n über k Rechner übersetzt dies in 4 über 3 und 4 über 2, und der Binomialkoeffizient Rechner zählt sie als 4 bzw. 6. Wenn wir diese Zahlen multiplizieren, stellen wir fest, dass es:

13 · 12 · 4 · 6 = 3744

mögliche Hände gibt, die ein Full House ergeben. Das sind zwar nicht allzu viele im Vergleich zu allen anderen Möglichkeiten, aber immerhin ist es 3744 Mal wahrscheinlicher als ein Royal Flush auf Kreuz.

Trotzdem empfehlen wir dir, dein Geld besser zu sparen als in Glücksspiele zu stecken!