Omni Calculator logo
Zuletzt aktualisiert:

Ähnliche Dreiecke Rechner

Neu

Inhalt

Was sind ähnliche Dreiecke?Finden ähnlicher Dreiecke: Gesetz der Ähnlichkeit von DreieckenWie berechent man die fehlende Seite eines ähnlichen Dreiecks?Wie berechnet man den Flächeninhalt eines ähnlichen Dreiecks?Wie man diesen Rechner für ähnliche Dreiecke benutztFAQs

Dieser Rechner für ähnliche Dreiecke hilft dir dabei, ein ähnliches Dreieck zu finden, indem du ein bekanntes Dreieck skalierst. Du kannst diesen Rechner auch benutzen, um die fehlende Länge eines ähnlichen Dreiecks zu ermitteln!

Bleib dran und lies diesen Artikel, in dem wir die Gesetze ähnlicher Dreiecke diskutieren und folgende Fragen beantworten:

  • Was sind ähnliche Dreiecke?
  • Die Suche nach ähnlichen Dreiecken: Wie kannst du feststellen, ob zwei Dreiecke ähnlich sind?
  • Wie berechnet man die fehlende Seite eines ähnlichen Dreiecks?
  • Wie berechnet man den Flächeninhalt eines ähnlichen Dreiecks?

Was sind ähnliche Dreiecke?

Zwei Dreiecke sind sich ähnlich, wenn ihre entsprechenden Seiten im gleichen Verhältnis stehen, was bedeutet, dass ein Dreieck eine skalierte Version des anderen ist. Natürlich sind die entsprechenden Winkel von ähnlichen Dreiecken gleich. Betrachte zum Beispiel die folgenden zwei Dreiecke:

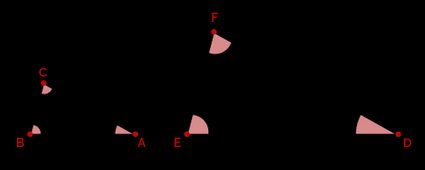
Die Seiten von ΔABC und ΔDEF sind proportional
Die Seiten von △ABC\triangle \text{ABC} und △DEF\triangle \text{DEF} sind proportional.

Beachte, dass die entsprechenden Seiten im Verhältnis zueinander stehen:

DEAB=EFBC=DFAC=2\frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC}} =\frac{\text{DF}}{\text{AC}} = 2

Deshalb können wir sagen: △ABC\triangle \text{ABC} ∼\sim △DEF\triangle \text{DEF}. Hier zeigt das Symbol ∼\sim an, dass die Dreiecke ähnlich sind.

Den Anteil der Ähnlichkeit bezeichnen wir als den Skalierungsfaktor (k)(k). Im obigen Beispiel ist der Faktor k=2k = 2. Wenn du Hilfe bei der Ermittlung von Verhältnissen brauchst, benutze unseren Verhältnisrechner.

Finden ähnlicher Dreiecke: Gesetz der Ähnlichkeit von Dreiecken

Wir wissen, dass zwei Dreiecke ähnlich sind, wenn eine der folgenden Bedingungen erfüllt ist:

  • Die entsprechenden Seiten des Dreiecks stehen im gleichen Verhältnis zueinander; oder
  • Die entsprechenden Winkel sind gleich.

Daraus können wir bestimmte Regeln ableiten, um festzustellen, ob zwei Dreiecke ähnlich sind:

  1. Seite-Seite-Seite (SSS): Wenn alle drei korrespondierenden Seiten der beiden Dreiecke in einem Proportionsverhältnis stehen, sind sie ähnlich. Diese Regel ist die einfachste und setzt voraus, dass du alle Seiten der Dreiecke kennst.
Die Seiten von $$\triangle \text{ABC}$$ und $$\triangle \text{DEF}$$ sind proportional.
Alle Seiten der Dreiecke △ABC\triangle \text{ABC} und △DEF\triangle \text{DEF} müssen bekannt und proportional zueinander sein.

Wir können dies mit einer ähnlichen Dreiecksformel ausdrücken:

DEAB=EFBC=DFAC=k\qquad \frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC}} =\frac{\text{DF}}{\text{AC}} = k

wobei kk der Skalierungsfaktor ist.

  1. Seite-Winkel-Seite (SWS): Wenn zwei korrespondierende Seiten zweier Dreiecke in Proportion stehen und ihre eingeschlossenen Winkel gleich sind, dann sind die Dreiecke ähnlich. Wir können diese Regel immer dann anwenden, wenn wir nur zwei Seiten eines Dreiecks und die dazugehörigen Winkel kennen.
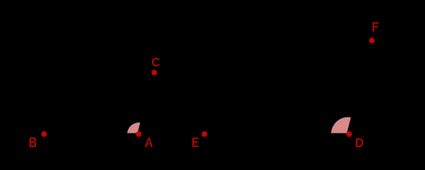
SWS-Ähnlichkeitskriterium.
Zwei beliebige Seitenpaare müssen im Verhältnis zueinander stehen und ihre eingeschlossenen Winkel müssen gleich sein.

Die Dreiecke im Bild oben sind ähnlich, wenn:

DEAB=DFAC=k,und∠BAC=∠EDF\qquad \begin{align*} &\frac{\text{DE}}{\text{AB}} = \frac{\text{DF}}{\text{AC}} = k, \text{und}\\\\ & \angle\text{BAC} = \angle\text{EDF} \end{align*}

Diese Regel ist praktisch, wenn die Dreiecke einen gemeinsamen Winkel haben, wie in der Abbildung unten:

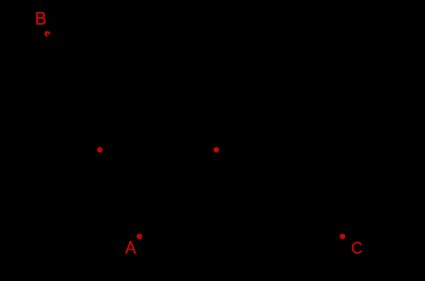
Zwei Dreiecke mit einem gemeinsamen Scheitelpunkt (gemeinsamer Winkel).
Die Dreiecke △ABC\triangle \text{ABC} und △PBQ\triangle \text{PBQ} haben einen gemeinsamen Winkel. In solchen Fällen ist es einfacher, das SWS-Kriterium zu prüfen.

Du kannst viele Dinge tun, wenn du nur die Seite-Winkel-Seite eines Dreiecks kennst. Erfahre mehr mit unserem SWS Dreieck Rechner 🇺🇸.

  1. Winkel-Seiten-Winkel (WSW): Wenn zwei beliebige Winkel zweier Dreiecke gleich sind und die entsprechenden Seiten zwischen ihnen im Verhältnis zueinander stehen, sind die Dreiecke ähnlich.
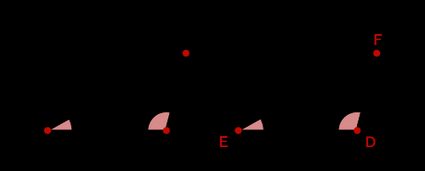
Zwei Dreiecke mit zwei Paaren von gleichen Winkeln und dem entsprechenden Seitenpaar im Verhältnis.
Zwei Dreiecke mit zwei gleichen Winkelpaaren sind ähnlich. Wenn du die entsprechenden Seiten kennst, kannst du ihren Faktor bestimmen.

Die Dreiecke im Bild oben sind ähnlich, wenn:

∠BAC=∠EDF,∠ABC=∠DEF, undDEAB=k\qquad \begin{align*} & \angle\text{BAC} = \angle\text{EDF}, \\ & \angle\text{ABC} = \angle\text{DEF}, \text{ und}\\\\ &\frac{\text{DE}}{\text{AB}} = k \end{align*}

Du kannst den dritten Winkel ermitteln, wenn du zwei beliebige Winkel in einem Dreieck kennst, indem du unseren Dreieckswinkel Rechner benutzt. Wir wissen, dass die Dreiecke ähnlich sind, wenn zwei Winkel in den Dreiecken gleich sind. Das bedeutet, dass wir nach der WSW-Kongruenzregel die Seiten nicht kennen müssen, solange die Winkel bekannt sind. Ohne die Seiten können wir jedoch den Skalierungsfaktor kk nicht bestimmen.

💡 Du musst den Flächeninhalt eines Dreiecks berechnen? Unser Dreiecksflächenrechner hilft dir dabei.

Wie berechent man die fehlende Seite eines ähnlichen Dreiecks?

Um die fehlende Seite eines Dreiecks mithilfe der entsprechenden Seite eines ähnlichen Dreiecks zu finden, befolge diese Schritte:

  1. Ermittle den Maßstabsfaktor k der ähnlichen Dreiecke, indem du das Verhältnis einer beliebigen bekannten Seite des größeren Dreiecks und der entsprechenden Seite des kleineren Dreiecks nimmst.
  2. Bestimme, ob das Dreieck mit der fehlenden Seite kleiner oder größer ist.
  3. Wenn das Dreieck kleiner ist, teilst du die entsprechende Seite im größeren Dreieck durch k, um die fehlende Seite zu erhalten. Andernfalls multipliziere die entsprechende Seite im kleineren Dreieck mit k, um die fehlende Seite zu finden.

Betrachte zum Beispiel die folgenden zwei ähnlichen Dreiecke.

Zwei ähnliche Dreiecke $$\triangle \text{ABC}$$ und $$\triangle \text{DEF}$$, bei denen die Seite $$\text{AC}$$ unbekannt ist.
Zwei ähnliche Dreiecke △ABC\triangle \text{ABC} und △DEF\triangle \text{DEF}, bei denen die Seite AC\text{AC} unbekannt ist.

Um die fehlende Seite zu finden, müssen wir zunächst ihren Skalierungsfaktor berechnen.

k=DEAB=84=2k = \frac{\text{DE}}{\text{AB}} = \frac{8}{4} = 2

Als Nächstes verwenden wir den Faktor für die Beziehung zwischen der fehlenden Seite AC und der entsprechenden Seite DF:

DFAC=k=2AC=DF2=62AC=3\begin{align*} \frac{\text{DF}}{\text{AC}} &= k=2\\[1em] \text{AC} &= \frac{\text{DF}}{2} = \frac{6}{2}\\[1em] \text{AC} &= 3 \end{align*}

🙋 Du kannst auch zwei rechtwinklige Dreiecke vergleichen und ihre Ähnlichkeit mit unserem Ähnlichkeit rechtwinkliger Dreiecke überprüfen Rechner 🇺🇸 feststellen.

Wie berechnet man den Flächeninhalt eines ähnlichen Dreiecks?

Um den Flächeninhalt eines Dreiecks A1 aus dem Flächeninhalt des ähnlichen Dreiecks A2 zu ermitteln, gehe folgendermaßen vor:

  1. Ermittle den Maßstabsfaktor k der ähnlichen Dreiecke, indem du das Verhältnis einer beliebigen bekannten Seite des größeren Dreiecks und der entsprechenden Seite des kleineren Dreiecks nimmst.
  2. Bestimme, ob das Dreieck mit dem unbekannten Flächeninhalt kleiner oder größer ist.
  3. Wenn das Dreieck kleiner ist, teilst du A2 durch das Quadrat des Skalierungsfaktors k, um A1 = A2/k2 zu erhalten. Ansonsten multipliziere A2 mit k2, um A1 = A2 ∙ k2 zu erhalten.

Wie man diesen Rechner für ähnliche Dreiecke benutzt

Jetzt, wo du gelernt hast, wie man die Länge eines ähnlichen Dreiecks findet, wie die Formel für ähnliche Dreiecke lautet und mehr, kannst du schnell herausfinden, wie dieser Rechner für ähnliche Dreiecke funktioniert.

Um zu prüfen, ob zwei bekannte Dreiecke ähnlich sind, benutze diesen Rechner wie folgt:

  1. Wähle Ähnlichkeit prüfen im Feld Typ.
  2. Wähle das Ähnlichkeitskriterium, das du möchtest. Du kannst zwischen Seite-Seite-Seite, Seite-Winkel-Seite und Winkel-Seite-Winkel wählen.
  3. Gib die Maße der beiden Dreiecke ein. Der Rechner ermittelt dann, ob sie ähnlich sind oder nicht.

Um mit diesem Rechner die Seite oder den Umfang ähnlicher Dreiecke zu bestimmen, gehe folgendermaßen vor:

  1. Wähle die fehlende Seite im Feld Typ aus.
  2. Gib die bekannten Maße, den Flächeninhalt, den Umfang und den Faktor der Dreiecke ein. Der Rechner für ähnliche Dreiecke ermittelt die unbekannten Werte.
FAQs

Sind alle gleichseitigen Dreiecke ähnlich?

Ja, wenn die entsprechenden Winkel zweier Dreiecke gleich sind, sind die Dreiecke ähnlich. Da jeder Winkel in einem gleichseitigen Dreieck gleich 60° beträgt, sind alle gleichseitigen Dreiecke ähnlich.

Was ist der Skalierungsfaktor von ähnlichen Dreiecken, deren Flächeninhalt 10 cm² und 20 cm² beträgt?

1,414. Um diesen Faktor auf der Grundlage der beiden Flächeninhalte zu ermitteln, gehst du folgendermaßen vor:

  1. Dividiere den größeren Flächeninhalt durch den kleineren und erhalte 20/10 = 2.
  2. Finde die Quadratwurzel aus diesem Wert, um den Skalierungsfaktor zu erhalten, also k = √2 = 1,414.
  3. Überprüfe dieses Ergebnis mit dem Rechner für ähnliche Dreiecke von Omni.
Check out 20 similar triangle calculators 🔺
30 60 90 triangle45 45 90 triangleArea of a right triangle...17 more