Dreieckswinkel Rechner

Du bist hier genau richrig, wenn du wissen möchtest, wie du den Winkel eines Dreiecks findest. Egal, ob du die drei Seiten eines Dreiecks (SSS), zwei Seiten und einen Winkel (SWS, SSW) oder nur zwei Winkel gegeben hast, dieses Tool ist die Lösung für deine Geometrieprobleme. Du findest die Erklärung der grundlegenden Gesetze für Dreieckswinkel: den Winkelsummensatz, den Außenwinkelsatz und den Winkelhalbierendensatz. Lies weiter, um zu verstehen, wie der Rechner funktioniert, und probiere ihn aus — die fehlenden Winkel eines Dreieckes zu finden war noch nie so einfach!

Es gibt verschiedene Möglichkeiten, die Winkel in einem Dreieck zu bestimmen, je nachdem, welche Werte gegeben sind:

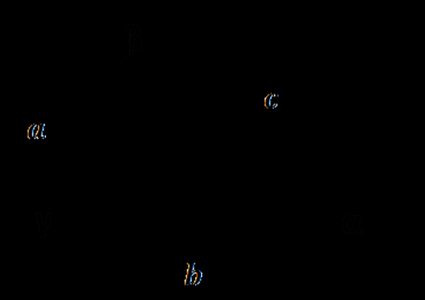
1. Gegebene drei Seiten (SSS)

Verwende den Kosinussatz:

also:

Den zweiten Winkel berechne wir folgendermaßen:

also:

Und den dritten Winkel:

also:

2. Gegebene zwei Dreiecksseiten und einen Winkel

Wenn der Winkel zwischen den gegebenen Seiten liegt (Kongruenzsatz SWS), kannst du direkt den Kosinussatz anwenden, um die unbekannte dritte Seite zu finden, und dann die obigen Formeln verwenden, um die fehlenden Winkel zu finden, z. B. bei a, b, γ:

• Berechne zuerst die fehlende Seite: $c = \sqrt{a^2 + b^2 - 2ab \cdot \cos(\gamma)}$,
• Setze $c$ in $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$ ein, und
• Finde dann $\beta$ mithilfe des Winkelsummensatzes für Dreiecke: $\beta = 180\degree- \alpha - \gamma$.

Wenn der Winkel nicht zwischen den gegebenen Seiten liegt (Kongruenzsatz SSW), kannst du den Sinussatz anwenden. Nehmen wir zum Beispiel an, dass wir $a$, $b$ und $\alpha$ kennen:

also:

• Wie du weißt, ist die Summe der Winkel in einem Dreieck gleich $180\degree$. Anhand dieses Winkelsummesatzes können wir den fehlenden Winkel finden: $\gamma = 180\degree- \alpha - \beta$.

3. Gegebene zwei Winkel

Das ist die einfachste Möglichkeit. Verwende einfach den Winkelsummensatz, um den fehlenden Winkel zu finden:

• $\alpha = 180\degree- \beta - \gamma$,
• $\beta= 180\degree- \alpha - \gamma$, und
• $\gamma = 180\degree- \alpha- \beta$.

Für jeden dieser Fällen kannst du natürlich auch unseren Winkel-Rechner für Dreiecke verwenden.

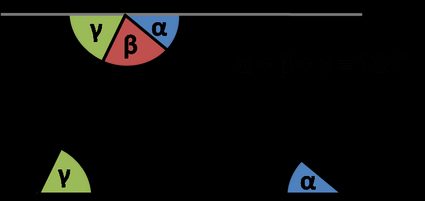
Der Satz besagt, dass sich die Innenwinkel eines Dreiecks immer zu $180\degree$ addieren:

Woher wissen wir das? Schau dir das Bild an: Die mit denselben griechischen Buchstaben bezeichneten Winkel sind kongruent, weil sie abwechselnd Innenwinkel sind. Die Summe der drei Winkel $\alpha$, $\beta$ und $\gamma$ beträgt $180\degree$, da sie eine Gerade bilden. Aber hey, das sind auch die drei Innenwinkel in einem Dreieck! Deshalb ist $\alpha + \beta+ \gamma = 180\degree$.

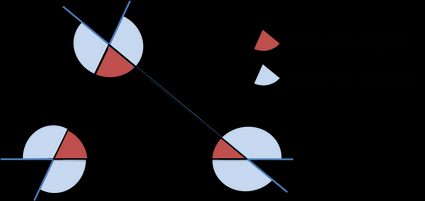
Ein Außenwinkel eines Dreiecks ist der Summe der gegenüberliegenden Innenwinkel gleich.

• Jedes Dreieck hat sechs Außenwinkel (zwei an jedem Eckpunkt, die gleich groß sind).
• Die Summe der Außenwinkel an jedem Eckpunkt beträgt immer $360\degree$.
• Ein Außenwinkel ist ein Ergänzungswinkel zu seinem benachbarten Innenwinkel.

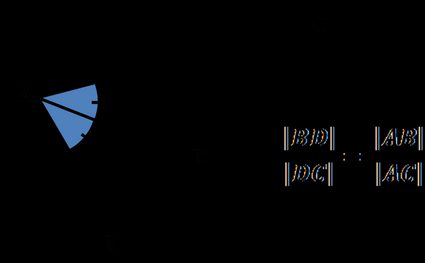
Der Winkelhalbierendensatz besagt, dass:

Eine Winkelhalbierende eines Dreieckswinkels teilt die gegenüberliegende Seite in zwei Segmente, die proportional zu den beiden anderen Dreiecksseiten sind.

Mit anderen Worten:

Das Verhältnis der Seitenlänge $\overline{BD}$ zur Seitenlänge $\overline{DC}$ ist gleich dem Verhältnis der Länge der Seite $\overline{AB}$ zur Länge der Seite $\overline{AC}$:

Okay, lass uns das, was wir gerade gelesen haben, in der Praxis anwenden. Angenommen, wir möchten die fehlenden Winkel in unserem Dreieck finden. Wie machen wir das?

1. Finde heraus, welche Formeln du verwenden musst. In unserem Beispiel haben wir zwei Seiten und einen Winkel angegeben. Wähle die Option Winkel und 2 Seiten im Rechner.
2. Gib die bekannten Werte ein. Wir wissen zum Beispiel, dass $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$ und $\alpha = 30\degree$ beträgt. Zur schriftlichen Berechnung verwende den Sinussatz:

also:

• Aus dem Winkelsummensatz können wir berechnen, dass $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51,\!06\degree= 98,\!94\degree$ beträgt.

3. Der Rechner findet die fehlenden Winkel im Dreieck, welche wir eben schriftlich berechnet haben: $\beta = 51,\!06\degree$ und $\gamma = 98,\!94\degree$. Das Tool ermittelt auch die fehlende Seitenlänge: $c = 17,\!78\ \mathrm{cm}$.

Ähnliche Überlegungen wie in diesem Rechner kommen auch in anderen Dreiecksberechnungen vor, zum Beispiel im WSW Kongruenzsatz Rechner 🇺🇸
und im SSW Kongruenzsatz Rechner 🇺🇸!