Pizzavergleich Rechner (alte Version)

Sieh dir den Pizzagröße Rechner! an, die neuere Version des Pizzavergleich-Rechners 🍕

Wie oft hast du dich schon gefragt, ob es besser ist, 2 mittelere Pizzen oder 1 große Pizza zu kaufen? Oder hast du nach „Pizzavergleich” gesucht, in der Hoffnung, Hilfe bei der richtigen Wahl zu finden, um deine Gelüste zu stillen? Pizzerien geben normalerweise den Durchmesser der Pizza an, was wir essen, ist aber nicht den Durchmesser. Wir essen auch nicht den Umfang, wir essen die Fläche der Pizza. Das ist ganz einfache Mathematik, die sich um die Gleichung Kreifläche = Radius² × π dreht. Oft haben wir es aber zu eilig oder einfach keine Lust, sie im Kopf auszurechnen, weshalb wir diesen Vergleichsrechner für Pizzagrößen entwickelt haben. Du erfährst, welche Mathematik hinter Pizzen steckt und wir visualisieren die Unterschiede von Umfang und Fläche in einem 30-cm-Pizza-Größenvergleich. Lies weiter, um zu lernen:

• wie du einen mathematisch korrekten Pizzavergleich durchführst,
• warum wir eine 30-cm-Pizza für den Größenvergleich verwenden und
• wie du den Rechner verwendest.

Was ist die Geometrie einer Pizza? Es dreht sich alles um Kreise. Ein Kreis ist eine Grundform, wohl die gleichzeitig einfachste und komplexeste, die du dir vorstellen kannst. Er besteht aus einer unendlichen Anzahl von Seiten, die in einem konstanten Abstand von einem zentralen Punkt angeordnet sind. Es erfordert besondere Formeln, um seinen Umfang oder seine Fläche zu berechnen, wobei immer die Konstante Pi (π) verwendet wird.

Davon ausgehend können wir die Formel für den Umfang eines Kreises herleiten:

Dabei ist $d$ der Durchmesser. So wird $\pi$ am häufigsten definiert: Indem du die Formel nach $\pi$ umstellst, erhältst du das Verhältnis zwischen dem Umfang eines Kreises und seinem Durchmesser.

In Bezug auf die Pizza ist der Umfang die Länge der Kruste (des äußeren Randes). Diese Größe interessiert uns im Moment nicht, denn die Köstlichkeit der Pizza liegt im Inneren der Pizza! Um diese Größe zu berechnen, müssen wir lernen, wie man die Fläche eines Kreises berechnet.

Dazu verwenden wir die folgende Formel:

Das Erste, was uns auffällt, ist, dass wir nicht mehr den Durchmesser, sondern den Radius verwenden. In der folgenden Abbildung kannst du sehen, wieso.

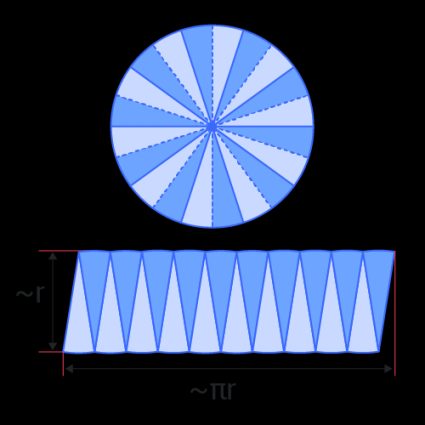
Unabhängig von der Darstellung kannst du bereits einen grundlegenden Unterschied in der Formel erkennen: Die Länge (der Durchmesser für den Umfang und der Radius für die Fläche) skalieren mit einem anderen Exponenten.

Was sind die Folgen eines unterschiedlichen Exponenten bei der Berechnung von Umfang und Fläche? Obwohl es nicht einfach ist, eine Länge (den Umfang) und eine Fläche (den Flächeninhalt) zu vergleichen, können wir anhand einer einfachen Gegenüberstellung sehen, wie sich die Verhaltensweisen unterscheiden.

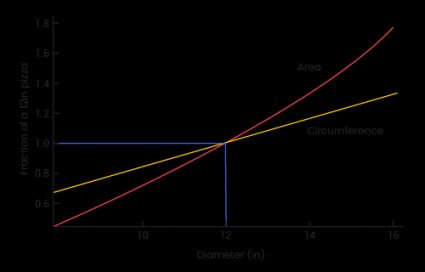
Diese Grafik zeigt das Wachstum des Umfangs und der Fläche einer Pizza als Funktion des wachsenden Durchmessers. Damit du eine Länge (den Durchmesser, mit der Einheit cm) und eine Fläche (mit der Einheit cm²) vergleichen kannst, haben wir diese Größen anhand einer durchschnittlichen 30-cm-Pizza (= 12 in) als Referenz skaliert. So können wir das Diagram in drei Bereiche unterteilen:

• Bei einem Durchmesser von 30 cm entsprechen der Umfang und die Fläche der Pizza der Referenz. Wir befinden uns also am Schnittpunkt der Kurve.
• Bei einem Durchmesser kleiner als 30 cm ist der Umfang größer als die Fläche, mit der Referenz verglichen. Das bedeutet, dass du bei einer Pizza, die kleiner als 30 cm ist, relativ mehr Kruste als Belag bekommst!
• Bei Durchmessern von mehr als 30 cm beginnt die Fläche schneller zu wachsen als der Umfang. Verglichen mit der Referenz haben größere Pizzen also mehr Fläche mit Belag als kleinere Pizzen.

Wie können also sagen, dass die Wahl einer größeren Pizza fast immer kostengünstiger ist. Wie in jeder anderen Branche auch, haben Pizzerien bei kleineren Produkten bessere Gewinnspannen/Preisaufschläge. Die folgende Tabelle zeigt, wie schnell die Fläche einer Pizza mit zunehmendem Durchmesser wächst. Demzufolge ist eine 40-cm-Pizza mehr als dreimal so groß wie eine 25-cm-Pizza. Gleichzeitig werden mit einer 61-Zentimeter-Monsterpizza mehr Menschen satt als mit zwei 40-Zentimeter-Pizzen oder fast sechs 25-Zentimeter-Pizzen.

Wenn du das nächste Mal eine Pizza bestellst, solltest du unseren Rechner verwenden. Du wirst dankbar sein, dass du gerechnet hast, wenn deine Bestellung ankommt. Jetzt kannst du nicht nur mit Rabatten Geld sparen!

Der Pizzavergleich-Rechner erfordert nur minimalen Aufwand von dir. Gib einfach den Durchmesser, den Preis und die Anzahl der kleineren Pizzen ein und wiederhole den Vorgang für die größere(n) Pizza/ Pizzen, die du in Betracht ziehst. Dieses Tool zeigt dir die Gesamtfläche und den Preis jeder Pizza an und wie sie im Vergleich zueinander stehen, ausgedrückt in Prozent. Wenn du nur die Flächen vergleichen möchtest, kannst du die Eingabe der Preise einfach weglassen. Die Einheiten kannst du nach Belieben zwischen metrischen und imperialen Maßeinheiten umschalten.