Balkenlast Rechner

Dieser Balkenlast-Rechner hilft dir, die Reaktionen an den Auflagern eines einfach gestützten Trägers aufgrund vertikaler Punktlasten oder Kräfte 🇺🇸 zu bestimmen. In diesem Rechner werden wir die folgenden Punkte untersuchen:

• Was eine Auflagerreaktion ist;
• Wie man die Auflagerreaktionen in einem Träger berechnet;
• Rechenbeispiele für Auflagerreaktionen; und
• Wie man die Tragfähigkeit eines Balkens mit diesem Rechner berechnet.

Zu wissen, wie man Auflagerreaktionen bestimmt, ist ein guter Ausgangspunkt für die Analyse von Trägern, z. B. für die Bestimmung der Trägerbiegung. Lies weiter, um mehr zu erfahren.

Nach Newtons drittem Bewegungsgesetz hat jede Kraft, die auf ein Objekt einwirkt, eine gleich große und entgegengesetzte Reaktion. Wenn du versuchst, auf etwas zu drücken, zum Beispiel auf eine Wand, fühlt es sich an, als würde die Wand auch auf dich zurückdrücken. Das ist genau das Phänomen, das Newtons drittes Gesetz der Bewegung beschreibt.

Im Bauwesen wirken Bauteile wie Träger und Säulen an den Punkten, an denen sie aufeinandertreffen, aufeinander ein. Stell dir einen Träger vor, der von zwei Säulen gestützt wird. Das Gewicht des Trägers drückt auf die Säulen, und aufgrund von Newtons drittem Bewegungsgesetz können wir auch sagen, dass die Säulen eine entsprechende Gegenkraft auf den Träger ausüben. Wir nennen diese Gegenkräfte Stützreaktionen.

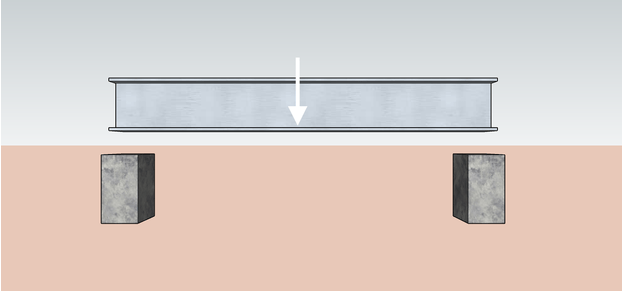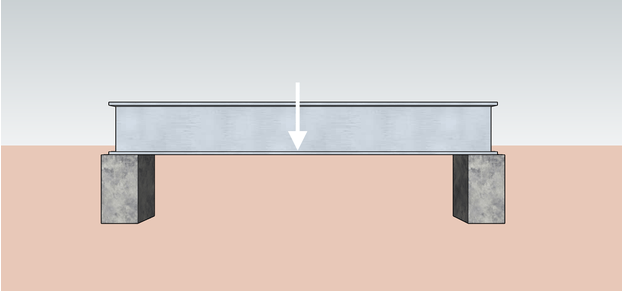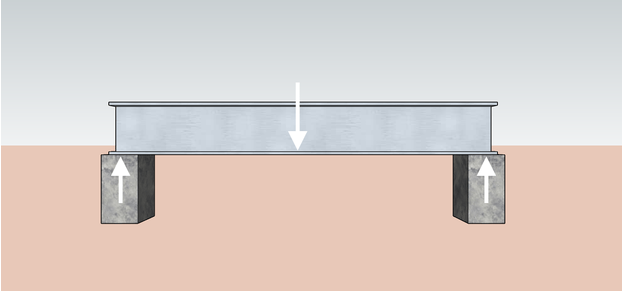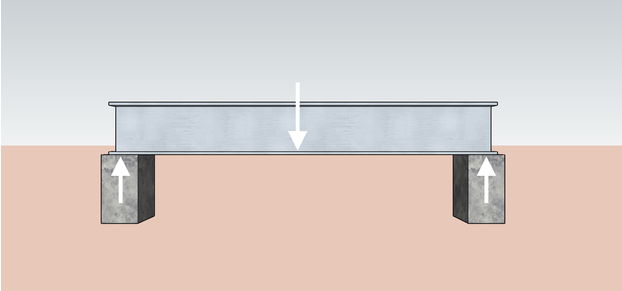
Du kannst dir einen Türkopf als den oben gezeigten Träger und die beiden Stollen (die vertikalen Stollen, auf denen der Türkopf aufliegt) als die beiden tragenden Strukturen des Türkopfes vorstellen. Erfahre mehr über die Größen von Türstürzen mit unserem Türsturz Größen Rechner 🇺🇸.

Bei einem einfach gestützten Träger können die Auflagerreaktionen an beiden Enden des Trägers entweder gleich oder unterschiedlich groß sein. Ihre Werte hängen von den Lasten ab, die auf den Träger wirken. Wenn sich mehr Lasten in einem geringeren Abstand zu einer Stütze befinden, erfährt die Stützkonstruktion mehr Kraft und damit eine größere Reaktion.

Da die Auflagerreaktionen in die entgegengesetzte Richtung wie die Kraft wirken, können wir sagen, dass sich das gesamte System im Gleichgewicht befindet. Das heißt, der Träger bewegt sich nicht und die Summe der Kräfte und Momente ergibt Null. Indem wir die Momente aufgrund der Belastung mit den Momenten aufgrund der Auflagerreaktionen gleichsetzen, können wir die Reaktionen an den Auflagern bestimmen.

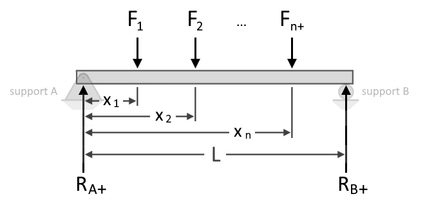
Genau wie bei der Berechnung des Drehmoments können wir auch eine Summierung der Momente an den einzelnen Stützen vornehmen, um die Reaktionen zu ermitteln. Im Folgenden werden die Momente an der Stütze A mit $\small \sum$ summiert, um die Reaktion an der Stütze B zu ermitteln ( $\small R_\text{B}$):

oder:

wobei:

• $F_1$, $F_2$, $F_3$ und $F_n$ – Punktlasten auf den Träger in den Abständen $x_1$, $x_2$, $x_3$ und $x_n$ vom Auflager A;
• $R_\text{B}$ – Reaktion an Stütze B; und
• $\text{Länge}$ – Länge des Trägers zwischen Träger A und Träger B.

Wenn wir die Gleichung umstellen, können wir $R_\text{B}$ wie folgt isolieren:

Da wir nun einen Ausdruck haben, um $\small R_\text{B}$ zu finden, und wir wissen, dass die Summe der aufgebrachten Kräfte gleich der Summe der Reaktionen ist, können wir nun auch die Reaktion an der Stütze A, $\small R_\text{A}$, mit den folgenden Gleichungen berechnen:

Da wir nun wissen, wie man Auflagerreaktionen in Trägern berechnet, können wir eine Beispielrechnung betrachten, um unser Wissen darüber zu festigen. 🙂

Angenommen, wir haben einen 4,0 Meter langen einfach gestützten Trägerbalken mit einer 10,0 Kilonewton (kN) Punktlast 2,0 Meter vom Träger A und einer weiteren 3,5 kN Punktlast 1,5 Meter vom Träger B, wie unten dargestellt:

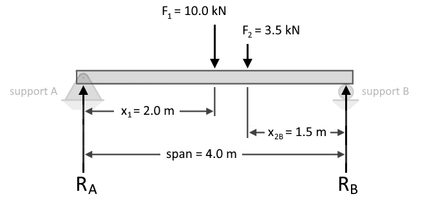
Für die Berechnung von $\small R_\text{B}$ formulieren wir die Gleichung des Momentengleichgewichts wie folgt:

Wenn wir die Kräfte addieren, erhalten wir:

Bitte beachte, dass wir für diese Summierung alle abwärts gerichteten Kräfte als positiv und alle aufwärts gerichteten Kräfte als negativ betrachtet haben. Anhand unserer obigen Berechnungen haben wir nun die Reaktionen an den Stützen A und B mit 6,3125 kN bzw. 7,1875 kN ermittelt.

Beachte auch, dass wir in diesem Beispiel zur Ermittlung der Auflagerreaktionen und im Trägerlastrechner davon ausgegangen sind, dass der Träger schwerelos ist. Wenn das Gewicht des Trägers jedoch angegeben ist, kannst du das Gewicht des Trägers als eine weitere nach unten gerichtete Punktlast in der Mitte oder im Schwerpunkt des Trägers betrachten.

Unser Rechner ist leicht und einfach zu bedienen. Alles, was du tun musst, ist die Länge des Trägers, die Größe der Punktlasten und ihre Abstände vom Stützträger A einzugeben. Zunächst siehst du nur Felder für zwei Lasten (Last 1 und Last 2), aber sobald du einen Wert für $\small x_2$ eingibst, werden die Felder für Last 3 angezeigt und so weiter.

Wenn du eine steigende Last eingeben möchtest, gib einfach einen negativen Wert für die Lastgröße ein. Insgesamt kannst du bis zu 11 Punktlasten in unseren Balkenlast-Rechner eingeben.

Ein einfach gestützter Träger ist ein Träger, der an jedem Ende zwei Stützen hat. Eine Stütze ist eine gelenkige Stütze, die nur einen Freiheitsgrad zulässt, nämlich die Drehung um die z-Achse (senkrecht zum Papier). Am anderen Ende befindet sich eine Rollenstütze, die zwei Freiheitsgrade ermöglicht: die horizontale Bewegung entlang der x-Achse und die Drehung um die senkrechte z-Achse.

Zur Bestimmung der Reaktionen auf einen einfach gestützten Träger:

1. Zeichne das Freikörperdiagramm des Trägers.

2. Summiere die Momente an einer Stütze, z. B. an der Stütze A:

   Σ(F_i × x_i) - R_yB × Balkenspannweite = 0,

   wobei:

   • F_i – Vertikalkräfte;
   • x_i – Abstand zwischen A und der Punktlast; und
   • R_yB – Vertikale Reaktion am Rollenträger B.

3. Um die vertikale Reaktion an A, R_yA, zu ermitteln, summiere die vertikalen Kräfte:

   ΣF_y = ΣF_i - R_yB - R_yA = 0.

4. Summiere die horizontalen Kräfte, um die horizontale Reaktion bei A R_xA zu finden:

   ΣF_y = ΣF_i - R_xA = 0.

Die Berechnung der Auflagerreaktionen ist entscheidend für das Verständnis der inneren Kräfte in einem Träger. Bei der Bemessung von Trägern müssen wir verstehen, wie sich die inneren Querkräfte und Biegemomente verhalten. Wenn wir wissen, wie diese Lasten entlang des Trägers variieren, können wir die daraus resultierenden Spannungen und Verformungen genau analysieren und vorhersagen. Das hilft uns, Träger zu entwerfen, die diesen Bedingungen standhalten und die strukturelle Integrität und Sicherheit gewährleisten.

Bei einem Träger mit einer gleichmäßig verteilten Gewichtsbelastung von 5 kN/m betragen die Reaktionen bei A und B jeweils 15 kN. Um dies zu berechnen:

1. Zeichne das Freikörperdiagramm des Trägers, einschließlich der äquivalenten Punktlast für das Gewicht.

2. Summiere die Momente am Bolzenlager A, um die vertikale Reaktion am Rollenlager B zu ermitteln:

   R_yB = 30 kN ∙ 3 m/6 m = 15 kN.

3. Summiere die vertikalen Kräfte, um die vertikale Reaktion an A zu ermitteln:

   R_yA = 30 kN - 15 kN = 15 kN.

4. Die horizontale Reaktion an der Stütze A, R_xA, ist Null.