Sexhörning – Kalkylator

Välkommen till vår sexhörningskalkylator – ett smidigt verktyg när du jobbar med regelbundna sexhörningar. Sexhörningen är en av de mest populära formerna i naturen, från bikakemönster till kakel och speglar, och dess användningsområden är nästan oändliga. Här förklarar vi inte bara varför denna sexsidiga polygon är så vanlig, utan också hur du ritar en perfekt sexhörning.

Med vår sexhörningskalkylator kan du enkelt utforska olika geometriska egenskaper och beräkningar – som att räkna ut arean eller omkretsen av en sexhörning – och få hjälp att analysera denna form på ett enkelt sätt.

Det kommer nog inte som en överraskning att en sexhörning (även kallad en polygon med 6 hörn) har exakt sex sidor. Detta gäller alla sexhörningar, det är just detta som definierar dem. Längden på sidorna kan däremot variera, utom i fallet med en regelbunden sexhörning, där alla sidor alltid är lika långa.

Vi kommer att gå djupare in på den här formen längre fram när vi tittar på hur man räknar ut arean av en sexhörning. Men redan nu kan vi säga att den regelbundna sexhörningen är den vanligaste typen av sexhörning, och den som oftast förekommer i naturen.

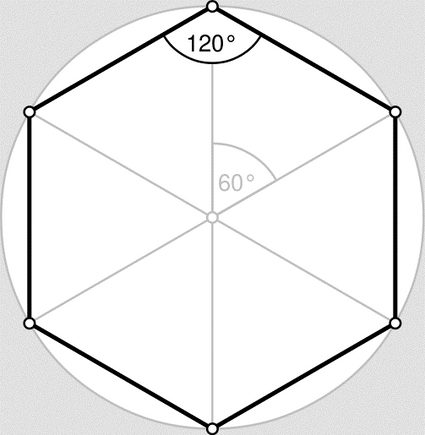
Vi kommer att ägna en hel sektion åt de viktigaste egenskaperna hos en regelbunden sexhörning, men först måste vi svara på frågan: Vad är en sexhörning? Genom att förstå detta får vi också verktygen för att beräkna arean på en sexhörning utan att bara följa formeln slaviskt. I stället kan vi använda smarta knep som bygger på andra former, till exempel kvadrater, trianglar och till och med parallellogrammer.

Som vi redan nämnt måste en regelbunden sexhörning ha lika långa sidor och alla inre vinklar måste vara lika stora. Alla sidlängder är lika giltiga (så länge alla sex sidor är lika långa!), så att räkna ut omkretsen är enkelt – du behöver inte ens använda vår omkrets av månghörning kalkylator 🇺🇸. Det räcker med formeln:

• omkrets = 6 × sida

Vinklarna i en godtycklig sexhörning kan ha olika värden, men summan av dem måste alltid bli 720° (du kan enkelt konvertera mellan enheter med vår vinkelomvandlare 🇺🇸). Eftersom en regelbunden sexhörning har lika stora vinklar innebär det att varje vinkel är exakt 120°. Detta är avgörande för att förstå varför sexhörningen är så vanlig i naturen, och det kommer också att hjälpa oss när vi ska förklara hur man räknar ut arean på en regelbunden sexhörning och tar fram formeln för det.

Nu ska vi gå igenom hur du kan räkna ut arean av en sexhörning på olika sätt. Det enklaste sättet är att använda vår sexhörningskalkylator, som dessutom innehåller ett inbyggt verktyg för att konvertera areaenheter. För dig som vill förstå uträkningen steg för steg, visar vi här hur man räknar ut arean för en regelbunden sexhörning, både med och utan areaformeln. Formeln för arean av en regelbunden polygon (oavsett antal sidor) är:

• area = apotem × omkrets / 2

Som påminnelse: apotem är avståndet från mitten av en sida till figurens mittpunkt. Den kan ses som höjden i den liksidiga triangel som bildas av en sida och två radier från mittpunkten. Det är alltså samma som det lodräta avståndet från mitten till en av sidorna.

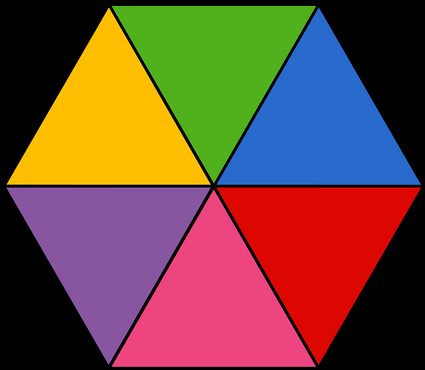
Om du inte kommer ihåg formeln kan du tänka på sexhörningen som uppdelad i sex liksidiga trianglar. För en regelbunden sexhörning är alla dessa trianglar liksidiga, vilket gör det enklare att räkna ut arean än om de hade varit likbenta eller t.ex. 45-45-90-trianglar som i ett kvadratiskt fall.

I en liksidig triangel är alla sidor lika långa, vi kallar denna längd a. Höjden i en sådan triangel är h = √3/2 × a, vilket alltså också är värdet på apotemen. (√ betyder kvadratroten.) Då får vi:

• A₀ = a × h / 2
• = a × √3/2 × a / 2
• = √3/4 × a²

Där A₀ är arean av en av trianglarna. Multiplicera med sex för hela sexhörningen:

• A = 6 × A₀ = 6 × √3/4 × a²

• A = 3 × √3/2 × a²

• = (√3/2 × a) × (6 × a) /2

• = apotem × omkrets /2

Så vi ser att vi landar i samma formel igen.

Vill du vara kreativ kan du leka med andra sätt att dela upp sexhörningen. Om du delar den rakt över (från hörn till hörn) får du två trapetser och kan räkna ut arean genom att summera deras ytor. Du kan också para ihop två intilliggande trianglar och få tre romber, eller dela upp hela figuren i en rektangel och två likbenta trianglar.

Prova gärna olika metoder, använd t.ex. bara rätvinkliga trianglar eller specialtrianglar för att räkna ut arean på olika sätt!

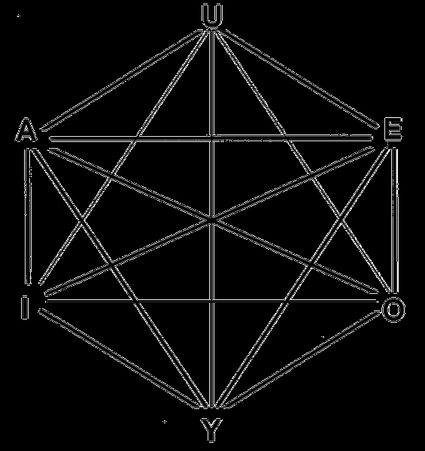
Det totala antalet diagonaler i en sexhörning är 9 – tre av dem är långa diagonaler som går rakt genom mittpunkten, medan de övriga sex brukar kallas för sexhörningens "höjd".
Vår sexhörningskalkylator hjälper dig att slippa räkna ut diagonallängderna själv. Så här beräknar du de två typerna av diagonaler:

• Långa diagonaler – Dessa går alltid genom sexhörningens mittpunkt. Som du ser i bilden ovan är deras längd lika med dubbla sidlängden:

  D = 2 × a

• Korta diagonaler – Dessa korsar inte mittpunkten utan förbinder två hörn med ett hörn mellan sig. Deras längd är: d = √3 × a.

Två andra viktiga mått i en sexhörning är radien för omkretscirkeln och incirkeln. Omkretscirkeln är den cirkel som går genom alla hörn på den regelbundna sexhörningen. Incirkeln är den största cirkel som ryms helt och hållet inuti sexhörningen.

• Omkretscirkelns radie (circumradius): För att hitta radien för en cirkel som omsluter en regelbunden sexhörning, behöver du bara mäta avståndet från sexhörningens mittpunkt (som också är cirkelns mitt) till vilket som helst av hörnen. Denna radie är helt enkelt: R = a.

• Incirkelns radie (inradius): Radien för en cirkel som ligger helt inuti en regelbunden sexhörning är lika med hälften av sexhörningens höjd, alltså apotemen: r = √3/2 × a.

Nu går vi över till något mer praktiskt och mindre matematiskt: hur du ritar en sexhörning. För en slumpmässig (oregelbunden) sexhörning är det enkelt, rita en sluten figur med sex sidor, och du är klar. Men för en regelbunden sexhörning är det lite klurigare, eftersom alla sidor måste ha exakt samma längd.

För att få ett perfekt resultat behöver du en passare. Börja med att rita en cirkel, och använd sedan samma radie för att göra markeringar längs cirkelns omkrets. Börja vid en godtycklig punkt och gör nästa markering genom att sätta passaren i föregående punkt, fortsätt så tills du har sex markeringar. Om du sedan binder ihop punkterna med räta linjer får du en regelbunden sexhörning. Du kan se en liknande process i animationen ovan.

Vår kalkylator för sexhörningar gör det enkelt att beräkna flera intressanta egenskaper hos denna sexsidiga figur. Du behöver bara fylla i ett enda värde, så räknar verktyget automatiskt ut resten, dessutom med inbyggd enhetsomvandling.

Vi har redan gått igenom de olika parametrarna, men här är en snabb översikt:

• Area – Ytan som täcks av sexhörningen;
• Sidlängd – Avståndet mellan två intilliggande hörn;
• Omkrets – Summan av alla sidors längd;
• Lång diagonal – Avståndet mellan två motsatta hörn;
• Kort diagonal – Avståndet mellan två hörn med ett hörn mellan dem;
• Radie för omskriven cirkel – Avståndet från mittpunkten till ett hörn (samma som radien);
• Radie för inskriven cirkel – Avståndet från mittpunkten till en sida (samma som apotemen).

Alla gillar praktiska tillämpningar, och sexhörningar är utan tvekan en av de mest använda formerna i världen. Bland mänskliga användningsområden är kanske det mest uppenbara (och minst spännande) sexkantiga kakelplattor för golv. Formen är perfekt eftersom sexhörningar passar ihop utan mellanrum och kan täcka en yta helt utan spill. Om du planerar ett sådant projekt rekommenderar vi att du använder vår golvberäknare 🇺🇸 och kvadratmeter kalkylator 🇺🇸 – två riktigt bra verktyg för att planera ditt materialbehov.

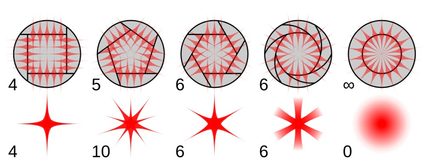
Nästa exempel gäller alla månghörningar, men det är ändå intressant att lyfta fram. Inom fotografi har öppningen till sensorn nästan alltid en polygonal form. Denna del av kameran kallas för bländaren, och den påverkar många egenskaper hos de bilder som kameran producerar. Den mest oväntade effekten är formen på mycket ljusstarka (punktformiga) objekt, något som uppstår på grund av diffraktion, och som kan ses i illustrationen ovan.

Ett av de mest värdefulla användningsområdena för hexagoner i modern tid, nära besläktat med det vi talade om inom fotografi, är inom astronomi. Ett av de största problemen vi stöter på när vi observerar avlägsna stjärnor är hur svaga de ser ut på natthimlen. Det beror på att, trots att de är mycket ljusstarka objekt, är de så långt borta att bara en liten del av deras ljus når oss – du kan läsa mer om detta i vår ljusstyrkekalkylator 🇺🇸. Utöver det påverkas deras ljus även av relativistiska effekter (liknande tidsdilatation och längdkontraktion), vilket gör att det når jorden med lägre energi än det hade vid utsändning. Denna effekt kallas för rödförskjutning.

Resultatet är att vi bara får en liten mängd energi med längre våglängd än önskat. Det bästa sättet att motverka detta är att bygga så stora teleskop som möjligt. Problemet är att det är nästintill omöjligt att tillverka en lins eller spegel i ett enda stycke som är större än ett par meter, och det blir snabbt ett logistiskt mardröm.

Lösningen är att bygga en modulär spegel av sexhörniga segment, precis som du kan se på bilderna ovan.

Att använda så stora speglar förbättrar både teleskopets upplösning och förstoringsfaktor, tack vare de geometriska egenskaperna hos ett "Cassegrain-teleskop". Så vi kan säga att tack vare regelbundna sexhörningar kan vi se längre, tydligare och med bättre precision än någonsin tidigare, något som aldrig hade varit möjligt med speglar i ett stycke.

Visste du förresten att sexhörniga lapptäcken också är en grej? Upptäck mer med Omnis hexagon quilt kalkylator 🇺🇸!

Honungsmönstret består av regelbundna sexhörningar placerade sida vid sida. De täcker hela ytan utan att lämna några hål emellan. Det här mönstret förekommer inte bara i bikakor (såklart!), utan också i många andra delar av naturen. Faktum är att det är så vanligt att man nästan kan säga att det är naturens standardform när motstridiga krafter samverkar och sfäriska former inte är möjliga på grund av problemets natur.

Från bisamhällen till bergssprickor och organisk kemi (till och med i livets byggstenar: proteiner) är regelbundna hexagoner den vanligaste polygonala formen som finns i naturen. Och det finns ett skäl till det: hexagonernas vinklar. Vinkeln 120º är den mest mekaniskt stabila av alla, och av en slump är det också den vinkel där sidorna möts i hörnen när vi ställer upp hexagoner sida vid sida. För en fullständig beskrivning av vikten av och fördelarna med vanliga hexagoner rekommenderar vi att du tittar på den här videon.

Sättet som 120°-vinklar fördelar krafter (och därmed spänning) mellan två av sexhörningens sidor gör formen mycket stabil och effektiv rent mekaniskt. Det är en stor fördel. En annan viktig egenskap hos regelbundna sexhörningar är att de kan täcka en yta helt utan mellanrum (tillsammans med regelbundna trianglar och kvadrater). Dessutom har den regelbundna sexhörningen minst omkrets i förhållande till största möjliga area av dessa ytfyllande former – vilket gör den mycket yteffektiv.

Ett fascinerande exempel i denna video är såpbubblor. När du blåser en bubbla med hjälp av vatten, tvål och lite luft, får den alltid en sfärisk form. Det beror på att en sfär har störst volym i förhållande till sin yta jämfört med alla andra former.

Men när bubblorna pressas ihop på en plan yta, tappar sfären sin effektivitetsfördel, eftersom en sfärisk form inte kan täcka ett tvådimensionellt utrymme helt. Näst bäst när det gäller förhållandet mellan volym och yta – och samtidigt bäst på att balansera den spänning som uppstår mellan bubblorna – är förstås vår fantastiska sexhörning.

Bubblor är ett intressant sätt att visualisera fördelarna med en sexhörning jämfört med andra former, men det är långt ifrån det enda exemplet. I naturen finns det, som vi nämnt, många exempel på sexhörniga formationer, oftast som ett resultat av spänningar och tryck i materialet. Vi kan tyvärr inte gå igenom alla exempel i detalj, men här är några platser där man kan hitta regelbundna sexhörningar i naturen:

• Bivaxkakor;
• Organiska föreningar;
• Hoppressade bubblor;
• Bergformationer (som Giant's Causeway);
• Insektsögon;
• ...