Räkna ut omkrets – Kalkylator
Med den här omkretskalkylatorn slipper du fundera på hur man räknar ut omkrets. Här nedanför hittar du formler för att beräkna omkretsen av tolv olika figurer – från cirkel och triangel till rektangel och kvadrat. Vi går också igenom vad omkrets egentligen är, med en tydlig förklaring. Testa kalkylatorn direkt eller kolla in dess systerverktyg: vår omfattande area kalkylator 🇺🇸.
Vad är omkrets?
Omkrets är längden runt en sluten geometrisk figur. Det är alltså den yttre kanten – den linje som omger formen helt. Ordet omkrets kommer från grekiskans perimetros, där peri betyder "runt" och metron betyder "mått". Eftersom omkretsen beskriver hur lång formen är längs kanten, anges den i längdenheter – till exempel meter, centimeter, tum eller fot.
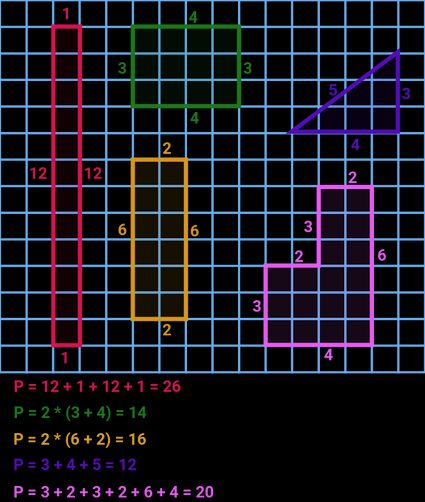
Hur räknar man ut omkrets? – Omkretsformler
Det vanligaste och enklaste sättet att räkna ut omkretsen är att addera alla sidor på figuren. Men i vissa fall – som med cirklar eller ellipser – finns det inga “sidor”, eller så är en eller flera längder okända. I det här avsnittet hittar du alla formler för att beräkna omkrets som används i den här kalkylatorn.
Vill du läsa mer om en specifik form? Scrolla vidare så hittar du förklaring, illustration och härledning för var och en av de tolv formerna som stöds i omkretskalkylatorn. Vi har också separata verktyg för varje figur – skriv bara in figurens namn i sökrutan längst upp på sidan.
Här är omkretsformlerna för de tolv geometriska figurerna i kalkylatorn:
-
Formeln för kvadrat: .
-
Formeln för rektangel: .
-
Formlerna för triangel:
- ; eller
- ; eller
- .
-
Formeln för cirkel: .
-
Formeln för cirkelsektor: ( är i radianer);
-
Formeln för ellips: ;
-
Formeln för fyrhörning/trapets: .
-
Formlerna för parallellogram:
- ;
- ; eller
- .
-
Formeln för romb:
- ; eller
- .
-
Formeln för deltoid: .
-
Formeln för ring: .
-
Formeln för regelbunden polygon: .
Omkrets av en kvadrat – formel

En kvadrat har fyra sidor som alla är lika långa. För att räkna ut omkretsen multiplicerar du helt enkelt sidans längd med :
Vill du slippa räkna själv? Vi har en omkrets av kvadrat kalkylator 🇺🇸 också!
Omkrets av en rektangel – formel

Formeln för omkretsen av en rektangel är nästan lika enkel som formeln för en kvadrat. Den enda skillnaden är att en rektangel har två par sidor med samma längd, en kort och en lång sid, i stället för fyra lika långa sidor:
Omkrets av en triangel – formel

Den enklaste formeln för att beräkna omkretsen av en triangel 🇺🇸 är att addera alla sidor:

Men du får inte alltid alla tre sidor från början. Vad gör du då? Oroa dig inte, du kan använda vår kalkylatorn för cosinussatsen 🇺🇸 för att räkna ut den saknade sidan:
Den tredje sidan kan sedan sättas in i formeln för att räkna ut triangelns omkrets:

Ett annat alternativ är att använda sinusregeln, om du har en sida samt de två vinklarna som ligger intill den:
Och:
Då kan triangelns omkrets uttryckas som:
Omkrets av en cirkel – formel (cirkelns omkrets)

Omkretsen av en cirkel kallas helt enkelt för cirkelns omkrets. Den vanligaste formeln för att räkna ut omkretsen använder radien:
Har du någonsin funderat på hur många varv ditt cykelhjul snurrar under en milslång cykeltur? Det är ett perfekt exempel på när du behöver använda formeln för att räkna ut omkrets. Ange radien på hjulet (hälften av hjuldiametern) och dela 10 miles med den omkrets du får fram – men glöm inte att omvandla längdenheterna så att de stämmer! Vill du vara extra noggrann kan du även ta med tjockleken på däcket i beräkningen.
Omkrets av en cirkelsektor – formel

Att räkna ut omkretsen av en cirkelsektor kan låta knepigt – är det bara cirkelbågen, eller är det bågen plus de två radierna? Tänk på vad omkrets faktiskt betyder! Omkretsen är summan av alla yttre kanter, så i det här fallet är det det senare:
där är vinkeln i radianer.
Omkrets av en ellips – formel (ellipsens omkrets)

Även om formeln för att räkna ut arean av en ellips är enkel och lätt att komma ihåg, är omkretsen av en ellips en av de krångligaste beräkningarna i hela den här kalkylatorn. Därför har vi valt att använda en av Ramanujans approximationer för att göra det möjligt att räkna ut omkretsen på ett smidigt sätt:
Där är den kortaste möjliga radien (lilla semiaxeln) och är den längsta möjliga radien (stora semiaxeln) för en ellips. En annan, mer exakt approximation av Ramanujan är:
Det finns också en enklare formel som använder en extra variabel, :
Den ser ut så här:
…eller så använder du helt enkelt vår kalkylator för att slippa räkna själv!
Omkrets av en trapets – formel

Om du vill räkna ut omkretsen av en oregälbunden trapets, finns det ingen särskild formel, du adderar helt enkelt de fyra sidlängderna:
Du kanske redan har märkt det – men den här formeln fungerar faktiskt för alla fyrhörningar, inte bara trapetser.
Det finns också specialfall där man kan förenkla beräkningen, till exempel med en likbent trapets, där du bara behöver känna till sidorna , och . Ett annat exempel är en rätvinklig trapets, där längden på de två baserna och ena sidan räcker – den fjärde sidan kan då räknas ut med hjälp av Pythagoras sats.
Omkrets av ett parallellogram – formel

I den här omkretskalkylatorn hittar du tre olika formler för att räkna ut omkretsen av ett parallellogram:
- Den mest direkta metoden, addera alla sidor:

- Formel för omkrets av ett parallellogram när du känner till en sida och båda diagonalerna:

- Omkretsen kan också beräknas utifrån bas, höjd och en valfri vinkel i parallellogrammen.
Omkrets av en romb – formel

Formeln för att räkna ut omkretsen av en romb är verkligen inte raketforskning , den är faktiskt samma som för en kvadrat!

Ett annat sätt att räkna ut omkretsen av en romb är att använda längden på dess diagonaler:
Prova gärna att härleda formeln själv! Du vet att en rombs två diagonaler är vinkelräta mot varandra och delar varandra mitt itu. Det innebär att romben kan delas upp i fyra likadana rätvinkliga trianglar. Varje triangel har kateter som är e/2 och f/2 långa. Allt du behöver göra är att räkna ut hypotenusan i en av dessa trianglar, den utgör samtidigt rombens sida. Sedan multiplicerar du resultatet med fyra för att få rombens omkrets:
Omkrets av en deltoid – formel

Formeln för omkretsen av en deltoid är mycket enkel – det är bara att addera alla sidor:
Omkrets av en ring – formel (annulus)

Eftersom omkrets definieras som formen yttre gräns, innebär det att vi för en ring (annulus) måste addera omkretsen av både den inre och den yttre cirkeln:
Omkrets av en regelbunden polygon – formel

I vår omkrets kalkylator har vi även lagt in en enkel formel för att räkna ut omkretsen av en regelbunden polygon:
där antalet sidor i polygonen. Du kan alltså till exempel räkna ut omkretsen av en femhörning (pentagon), sexhörning (hexagon) eller åttahörning (oktogon).
För polygoner med upp till 12 sidor visas dessutom figurens namn automatiskt i verktyget, hur bra som helst!
Om du vill räkna ut omkretsen av vilken som helst polygon, är det bara att addera längden på alla sidor:
där , , ..., är längderna på polygonens sidor, och är summatecknet (summan från till ).
Alternativt kan du använda hörnpunkternas koordinater:
Med och .
Vanliga frågor
Hur räknar jag ut omkretsen av oregelbundna figurer?
För att beräkna omkretsen av en oregelbunden figur, gör du så här:
- Mät längden på alla yttre sidor, både raka och böjda.
- Om figuren innehåller cirkulära bågar, mät radien och medelpunktsvinkeln, alltså vinkeln mellan de två radierna som går till bågens ändpunkter.
- Använd formeln för cirkelns omkrets för att räkna ut längden av bågen, och ta den del som motsvarar vinkeln.
- Addera längden på alla sidor (raka och böjda) för att få den totala omkretsen.
Kan jag räkna ut arean om jag bara känner till omkretsen?
Generellt sett, nej. Det går oftast inte att beräkna arean enbart utifrån omkretsen. Det gäller särskilt för figurer som rektanglar, parallellogram, deltoider och trapetser, där flera olika former kan ha samma omkrets men olika area. Men för vissa specifika figurer, som kvadrater, regelbundna polygoner (t.ex. hexagoner) och cirklar, går det att räkna ut sidan (eller radien) utifrån omkretsen och därifrån beräkna arean.
Vad är omkretsen av en rektangulär byggnad som är 20 × 15 meter?
Omkretsen är 70 meter. För att komma fram till det adderar du längden på alla fyra sidor av byggnaden. De två längre sidorna är 20 meter vardera, vilket ger totalt 40 meter. De två kortare sidorna är 15 meter vardera, vilket ger 30 meter. Tillsammans blir det 40 meter + 30 meter = 70 meter, precis som förväntat.