Diagonal i rektangel – Kalkylator

Vår kalkylator för diagonal i rektangel är ett kraftfullt verktyg som snabbt hjälper dig att räkna ut både diagonalen och andra mått i en rektangel. Har du stött på ett problem där du inte vet hur man räknar ut diagonalen i en rektangel? Prova att fylla i några värden i fälten bredvid, eller läs vidare för att upptäcka vilka formler för rektangelns diagonal som finns.

I figuren nedan ser du en typisk rektangel. Vi har markerat fem grundläggande mått som beskriver en rektangel. Du kan använda dessa för att ta fram formeln för diagonalen i en rektangel. Dessa är:

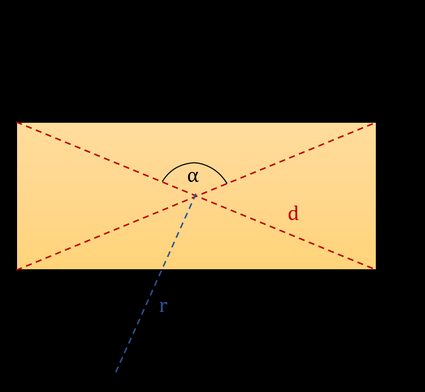
• l - Längd;
• w - Bredd;
• α - Vinkeln mellan diagonalerna;
• r - Cirkelns radie;
• d - Diagonal;

och två ytterligare mått visas inte i figuren:

• A - Area;
• P - Omkrets.

Ordet rektangel kommer från latinet rectangulus, som är en sammansättning av orden rectus (rak, korrekt) och angulus (vinkel). Namnet speglar att en rektangel är en fyrhörning med fyra räta vinklar (4 × 90° = 360°). Dess motstående sidor är parallella och lika långa, och dess två diagonaler korsar varandra i mitten och är lika långa.

Ett kvadrat är ett specialfall av en rektangel. Den definieras som en rektangel där alla fyra sidor har samma längd, eller alternativt att vinkeln mellan diagonalerna är rät. Prova gärna våra kalkylatorer för kvadrater, till exempel kvadrat-kalkylatorn 🇺🇸, som snabbt kan räkna ut både omkrets, area och diagonal baserat på sidans längd.

Mittpunkten i en rektangel ligger lika långt från alla hörn, vilket innebär att du alltid kan rita en omskriven cirkel runt en rektangel. Däremot kan du bara rita en inskriven cirkel i en rektangel om den är en kvadrat.

För att bestämma diagonalen i en rektangel måste du:

1. Skriva ner rektangelns sidor, som vi betecknar med w och l.
2. Kvadrat dessa två värden. Det vill säga beräkna l² och w².
3. Addera de två kvadrerade värdena från steg 2.
4. Ta kvadratroten av resultatet.
5. Nu är det klart! Du har just hittat längden på diagonalen i din rektangel.

Varför fungerar den här metoden?

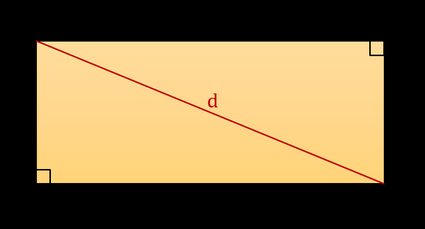
För att härleda formeln för diagonalen i en rektangel kan du tänka dig att rektangeln delas upp i två likadana rätvinkliga trianglar, alltså trianglar där en av vinklarna är 90°. Varje sådan triangel har sidor med längderna l (längd) och w (bredd) samt en hypotenusa d som motsvarar rektangelns diagonal. Med hjälp av Pythagoras sats, som du också hittar i vår kalkylator för Pythagoras sats 🇺🇸, kan du skriva sambandet:

d² = l² + w²

och för att få fram den färdiga formeln för diagonalen, tar du kvadratroten:

d = √(l² + w²)

Nu vet du exakt hur du räknar ut diagonalen i en rektangel med hjälp av sidorna.

Vår kalkylator för diagonal i rektangel låter dig använda nästan vilka enheter du vill. Kolla in vår längdomvandlare 🇺🇸 eller areaomvandlare 🇺🇸 för att se hur du enkelt växlar mellan olika enheter, både metriska (SI) och imperiala.

Ibland har du inte båda sidornas längder givna. Hur räknar du då ut diagonalen i en rektangel? Svaret hittar du med vår kalkylator för rektangelns diagonal. Låt oss först gå igenom tre grundläggande formler:

1. Area av en rektangel: A = w × l.
2. Rektangelns omkrets: P = 2 × w + 2 × l.
3. Radie för omskriven cirkel: r = d/2.

Med dessa formler kan vi härleda flera olika sätt att räkna ut diagonalen i en rektangel, beroende på vilka värden du har:

1. Givet längd och bredd:

   d = √(l² + w²)

2. Givet längd eller bredd och area:

   d = √(A²/l² + l²) eller d = √(A²/w² + w²)

3. Givet längd eller bredd och omkrets:

   d = √(2l² - P × l + P²/4)) eller d = √(2w² - P × w + P²/4)

4. Givet längd/bredd och vinkel:

   d = w / sin(α/2) eller d = l / cos(α/2)

5. Givet area och omkrets:

   d = ½√(P² - 8 × A)

6. Givet area och vinkel:

   d = √(2 × A / sin(α))

7. Givet omkrets och vinkel:

   d = P / (2 × sin(α/2) + 2 × cos(α/2))

8. Givet radien för omskriven cirkel:

   d = 2 × r

Obs: Vinkeln α mellan diagonalerna är den som ligger mittemot sidan med längden l, som du kan se i den första figuren. Tänk också på att kalkylatorn utgår från att rektangelns längd är större än dess bredd.

Visste du att det finns en speciell typ av rektangel som kallas gyllene rektangel? Kolla in vår gyllene rektangel kalkylator 🇺🇸 för att lära dig hur du kan konstruera en sådan!