Beräkna volym i tank

Q: Hur räknar man ut volymen på en vattentank?

Du kan använda Omni Calculators verktyg tankvolym kalkylator eller göra det manuellt så här: Ta reda på tankens inre radie och höjd . Kvadrera radien (multiplicera den med sig själv) och multiplicera sedan med pi (≈ 3,1416). Nu har du tankens area . Multiplicera arean med höjden – resultatet är tankens volym .

Q: Hur räknar man ut motorvolym (slagvolym)?

Bilentusiaster kallar det slagvolym (engine displacement), och du kan räkna ut det så här: Ta reda på volymen för en av cylindrarna i motorn. Du kan använda Omni Calculators tankvolym kalkylator eller själv mäta cylinderns radie och slaglängd (piston stroke). Kvadrera radien, multiplicera med π (≈ 3,1416) och därefter med slaglängden. Då får du volymen för en cylinder. Multiplicera volymen för en cylinder med antalet cylindrar i motorn, det ger dig den totala motorvolymen.

Q: Hur länge räcker vattnet i en tank?

Det beror på hur mycket vatten du har lagrat och hur snabbt det förbrukas. Så här räknar du ut det: Beräkna volymen på din vattentank med Omni Calculators tankvolym kalkylator. Få resultatet i liter. Ta reda på hur många liter vatten du förbrukar per dag . Dividera mängden vatten i tanken med din dagliga förbrukning. Resultatet visar hur många dagar ditt vatten räcker.

Q: Varför föredrar vi cylindriska vattentankar framför fyrkantiga?

Det finns två huvudsakliga skäl till att cylindriska tankar ofta är att föredra framför rektangulära: Cylindriska tankar tål tryck och påfrestningar bättre än fyrkantiga tankar. Det innebär att tillverkare kan använda mindre material, vilket gör dem både starkare och mer kostnadseffektiva. Rektangulära tankar är svårare att rengöra , särskilt i hörnen där smuts och bakterier lätt samlas.

Q: Hur stor är volymen på ett oljefat?

218,7 liter. Ett oljefat har en diameter på 0,572 meter och en höjd på 0,851 meter. Sätt in värdena i formeln för volymen av en cylinder: volym = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 liter

Skapare

Hanna Pamuła, doktor

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Översättare

Emmyline Rundberg

Granskare

Bogna Szyk

Bogna is the chief operating officer at Omni Calculator, where she helps keep things running smoothly and ideas moving forward. With a background in civil engineering and a knack for organizing chaos, she brings structure and strategy to everything she does. After hours, you’ll likely find her dancing zouk or crafting the next twist in a D&D campaign. See full profile

Check our editorial policy

och Jack Bowater

Med den här tankvolym kalkylatorn kan du enkelt beräkna volym i tank, oavsett form. Välj mellan tio olika tankformer, från vanliga rektangulära och cylindriska behållare till kapsel- och elliptiska tankar. Du kan till och med räkna ut volymen i konbotten-tankar (frustum). Ange bara måtten på din behållare så räknar verktyget automatiskt ut den totala tankvolymen. Om du vill veta hur mycket som faktiskt är fyllt, kan du också ange fyllnadshöjden. Kalkylatorn visar då den fyllda volymen direkt.

Nyfiken på hur uträkningarna görs? Scrolla ner så hittar du alla formler för kapseltankar, elliptiska tankar, konbotten-tankar (även kallade koniska tankar), och många fler.

Letar du efter andra typer av volymberäkningar? Kolla in vår volym kalkylator för vanliga tredimensionella former. Du kan också testa vår volym kalkylator för vanliga tredimensionella former. Du kan också testa vår akvariekalkylator 🇺🇸 och poolvolym kalkylator 🇺🇸 för mer specifika behov i vardagen.

Så använder du tankvolym kalkylatorn

Den här kalkylatorn är ett enkelt verktyg som hjälper dig att både beräkna volym i tank och hur mycket av tanken som är fylld. Du kan välja mellan tio olika tankformer:

Vertikal cylinder;
Horisontell cylinder;
Rätblock (rektangulär låda);
Vertikal kapsel;
Horisontell kapsel;
Vertikal oval (elliptisk);
Horisontell oval (elliptisk);
Konbotten;
Kontopp;
Frustum (stympad kon, trattformad)

”Men hur använder jag tankvolym kalkylatorn?” Undrar du kanske. Här är ett enkelt exempel:

Välj tankens form. Låt oss säga att vi vill beräkna volymen i en vertikal cylindertank – välj det alternativet i rullgardinsmenyn. En schematisk bild visas nedanför, så att du kan kontrollera att det är rätt typ av tank.
Fyll i tankens mått. I vårt exempel skriver vi in höjden och diametern: till exempel $80\ \mathrm{cm}$ och $60\ \mathrm{cm}$ . Om du även vill veta hur mycket vätska som faktiskt finns i tanken, kan du ange fyllnadshöjden – till exempel $70\ \mathrm{cm}$ .
Kalkylatorn räknar automatiskt ut tankvolymen! I det här fallet kanske den totala volymen är $226\ \mathrm{ liter}$ ,och den fyllda volymen $198\ \mathrm{ liter}$ . Du kan när som helst byta enhet genom att klicka på måttenheten i fältet. Smidigt, eller hur?

Volymformel för cylindrisk tank

För att beräkna den totala tankvolymen i en cylindrisk behållare behöver vi bara känna till cylinderdiametern (eller radien) samt höjden på cylindern. Om tanken ligger ned kan höjden även kallas längd.

Vertikal cylindertank

Vi kan beräkna den totala tankvolymen för en vertikal cylindertank med den vanliga volymformeln, alltså basytan multiplicerad med höjden. Eftersom basen är en cirkel, beräknas dess area enligt den välkända formeln: $\pi \times \mathrm{radie}^2$ . Därför ser formeln för volymen i en vertikal cylindertank ut så här:

\begin{split} V_{\scriptsize{\mathrm{\tiny vertikal\ cylinder}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h, \end{split}

där:

$r$ — Radien på basen;
$h$ — Höjden på cylindern.

Om vi vill beräkna den fyllda volymen, behöver vi bara räkna ut volymen av en "kortare" cylinder – så enkelt är det!

\begin{split} V_{\scriptsize{\mathrm{\tiny vertikal\ cylinder}}} &= \pi \times r^2 \times f\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times f, \end{split}

där $f$ är höjden på den fyllda delen av cylindern.

Horisontell cylindertank

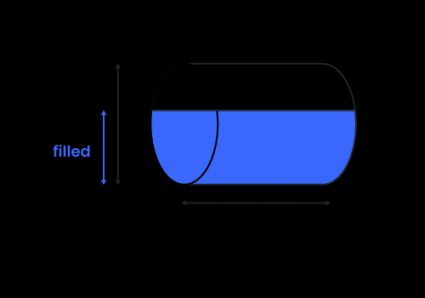
Den totala volymen i en horisontell cylindertank beräknas på liknande sätt som för en vertikal cylinder. Det är arean av den cirkelformade ändytan multiplicerat med cylinderns längd:

\begin{split} V_{\scriptsize{\mathrm{\tiny horisontell\ cylinder}}} &= \pi \times r^2 \times l\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times l, \end{split}

där $l$ är cylinderns längd.

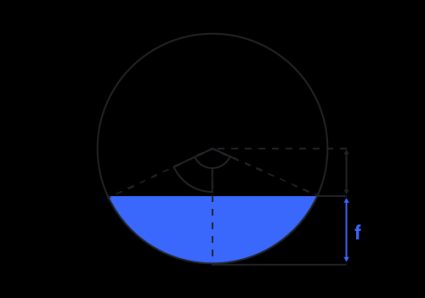
Tvärsnitt av en delvis fylld cylindrisk tank. — Tvärsnitt av delvis fylld cylindertank.

Saker och ting blir lite mer komplicerade när vi vill beräkna volymen i en delvis fylld horisontell cylindertank. Först måste vi räkna ut basytan, alltså arean av den cirkelsektor som täcks av vätskan:

A_{\mathrm{\tiny segment}} = \frac{1}{2}\times r^2 \times (\theta-\sin(\theta)),

där $r$ är basens radie och $\theta$ är medelpunktsvinkeln för det cirkulära segmentet. Vinkeln $\theta$ kan beräknas med hjälp av cosinusformeln:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f},

där $f$ är höjden på den fyllda delen av basen.

Alltså får vi:

\theta= 2\times \arccos\left(\frac{r-f}{f}\right)

Och slutligen, formeln för volymen i en delvis fylld horisontell cylindertank $V_{\scriptsize{\mathrm{fhc}}}$ är:

\small V_{\scriptsize{\mathrm{fhc}}} = 0.5\times r^2\times(\theta -\sin(\theta))\times l,

där:

\theta = 2\times \arccos\left(\frac{r-f}{r}\right)

Om cylindern är mer än halvfull är det enklare att subtrahera volymen av den tomma delen från den totala tankvolymen. På så sätt slipper man räkna på den större cirkelsektorn och får samma resultat med mindre beräkning.

Volymkalkylator för rektangulär tank (rätblock)

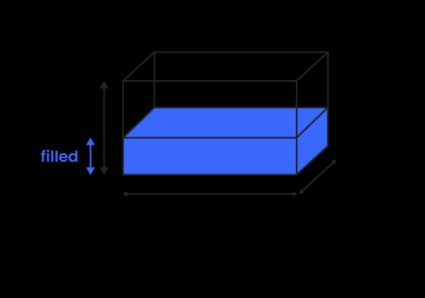
Om du undrar hur man beräknar volymen i en rektangulär tank (även kallad rätblock, låda eller rektangulärt hexaeder), så behöver du inte leta längre! Du kanske känner igen den här typen av tank som en rektangulär tank, men det är egentligen inte helt korrekt. En rektangel är en tvådimensionell form och har därför ingen volym. Den korrekta geometriska termen är rätblock.

För att beräkna volymen i ett rätblock multiplicerar du helt enkelt alla tre mått:

V_{{\mathrm{rätblock}}} = h\times w\times l,00

där:

$h$ — Höjden på tanken;
$w$ — Bredden;
$l$ — Längden på tanken.

Om du vill veta vätskevolymen i en rektangulär tank, byter du helt enkelt ut höjden mot fyllnadshöjden i formeln för rektangulär volym. Då får du formeln för en delvis fylld rektangulär tank: $V_{\scriptsize{\mathrm{rpf}}}$ :

V_{{\mathrm{rpf}}} = f\times w\times l,

där $f$ är höjden på den fyllda delen.

För den här tankvolym kalkylatorn spelar det ingen roll om tanken är placerad horisontellt eller vertikalt. Det viktiga är att du säkerställer att fyllnadshöjden och höjden mäts längs samma axel.

Formel för volymen av en kapsel

I vår kalkylator definieras en kapsel som två halvsfärer separerade av en cylinder. För att beräkna den totala volymen i en kapseltank adderar du volymen av cylinderdelen och volymen av sfären:

V_{\scriptsize{\mathrm{cap}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!l\right)

Beroende på tankens placering kommer beräkningen av fylld volym att skilja sig något:

1. För horisontell kapseltank

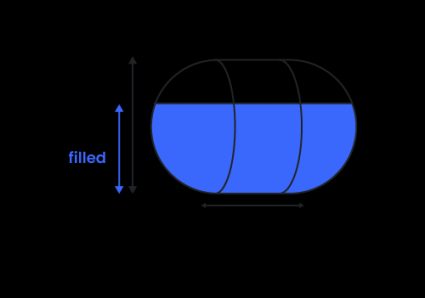
Horisontell kapseltank med markerade mått.

Eftersom halvsfärerna i båda ändar av tanken är identiska, bildar de tillsammans en sfärisk kupa. För att beräkna vätskevolymen i en fylld horisontell kapseltank adderar du volymen från den sfäriska kupan, $V_{\scriptsize{\mathrm{sph\ hf}}}$ till volymen från den horisontella cylinderdelen, $V_{\scriptsize{\mathrm{fhc}}}$ . Den totala vätskevolymen i kapseltanken uttrycks då som: ( $V_{\scriptsize{\mathrm{cap\ hf}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{cap\ hf}}} = V_{\scriptsize{\mathrm{fhc}}}+V_{\scriptsize{\mathrm{sph\ hf}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times l \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right), \end{split}

där:

$d$ — Tankens diameter;
$f$ — Fyllnadshöjd;
$\theta$ — Vinkeln som motsvarar den fyllda sektorn i den cylindriska delen av tanken.

2. För vertikal kapseltank

Formeln varierar beroende på fyllnadshöjden. I alla kommande formler för den här typen av tank kommer vi att använda följande storheter:

$d$ - Diametern på tanken;
$f$ — Höjden som vätskan når upp till;
$l$ — Längden på den cylindriska mittsektionen.

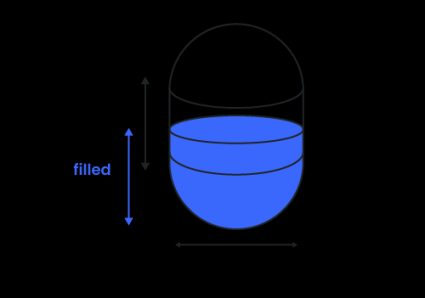
Om $f < d/2$ , befinner sig vätskan endast i den undre halvsfären, och vi behöver därför endast använda formeln för volymen av en sfärisk kupa:

\\[2em] V_{\scriptsize{\mathrm{cap\ f}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]

Om $d/2 < f < d/2 +l$ , behöver vi addera volymen av den nedre halvsfären och volymen av en kortare cylindrisk del (den del av mittsektionen som är fylld):

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}

Om $d/2 + l < f$ , betyder det att den nedre halvsfären och hela cylindern är fyllda, och att endast en del av den övre halvsfären är tom. Då kan vi enkelt subtrahera volymen av den tomma sfäriska kupan från hela tankens volym:

\begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\times(l+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (l+d-f)\right) \end{split}

Volym för elliptisk tank (oval tank)

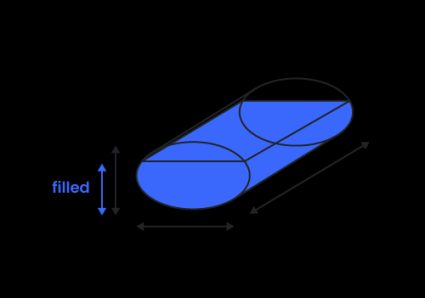
Horisontell oval tank med markerade mått.

I vår kalkylator definierar vi en oval tank som en cylindrisk tank med elliptisk bas, och inte som en stadionformad tank (vilket ibland används som definition). För att beräkna den totala volymen i en elliptisk tank multiplicerar du arean av ellipsen med tankens längd:

V_{\scriptsize{\mathrm{ellips}}} = \pi\!\times\!w\!\times\!l\!\times\!\frac{h}{4},

där:

$w$ — Bredden på tanken;
$h$ — Höjden på tanken;
$l$ — Längden på tanken.

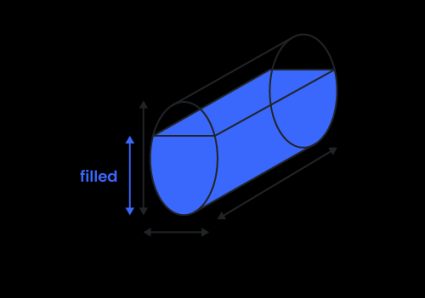
Äntligen en enkel formel! Tyvärr är det inte lika enkelt att beräkna volymen i en delvis fylld oval tank – varken i horisontellt eller vertikalt läge. För att räkna ut den fyllda volymen behöver du använda formeln för arean av ett ellipssegment, och sedan multiplicera resultatet med tankens längd:

\begin{split} &V_{\scriptsize{\mathrm{ellips\ fylld}}} = l\!\times\!h\!\times\!\frac{w}{4}\\[1em] &\qquad\times\!\left[\arccos\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Volym för frustum – tank i form av en stympad kon

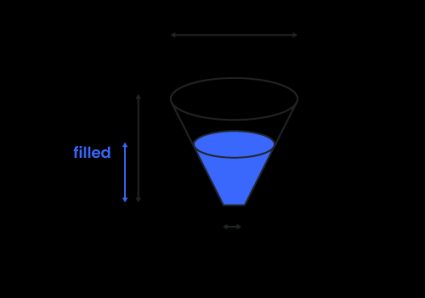
För att beräkna volymen av en stympad kon (även kallad frustum), en form du också hittar i vår stympad kon kalkylator 🇺🇸), använder du följande formel:

\begin{split} &V_{\scriptsize{\mathrm{stympad\ kon}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cone}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\!+\! \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right), \end{split}

där:

$d_{\mathrm{topp}}$ – Övre diameter på den stympade konen;
$d_{\mathrm{botten}}$ – Nedre diameter på den stympade konen;
$h_{\mathrm{kon}}$ – Höjden på tanken.

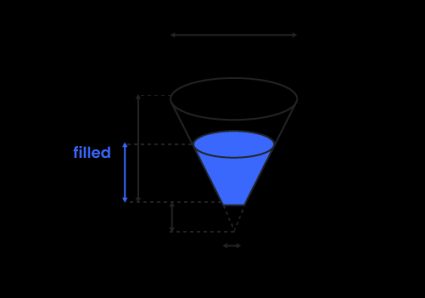
Frustumtank med markerade mått och vätskenivå. — Frustum-tank med markerade mått och vätskenivå.

För att beräkna volymen i en delvis fylld frustum-tank (stympad kon) med en given fyllnadshöjd, börjar du med att räkna ut radien vid vätskans övre nivå:

R = \frac{1}{2} \times d_{\mathrm{top}}\times \frac{f+z}{h_{\mathrm{cone}}+z},

där:

z = h_\mathrm{cone} \times \frac{d_{\mathrm{bot}}}{d_{\mathrm{top}}-d_{\mathrm{bot}}}

(Du kan härleda formeln med hjälp av likformiga trianglar.)

Därefter kan du beräkna volymen av den vätskefyllda delen av frustumen med formeln:

\begin{split} &V_{\scriptsize{\mathrm{ff}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{bot}}}{2} + \left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right) \end{split}

Tankar med konisk topp eller botten

Att beräkna den totala volymen i en konbotten-tank är inte särskilt svårt, du behöver bara addera volymen av den stympade konen (frustumdelen) och volymen av den cylindriska delen:

\begin{split} &V_{\scriptsize{\mathrm{cone\ b}}} = V_{\scriptsize{\mathrm{frustum}}} + V_{\scriptsize{\mathrm{cylinder}}}\\[1em] & =\frac{1}{3}\times\pi\times h_{\mathrm{cone}} \times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\times\left(\frac{d_{\mathrm{top}}}{2}\right)^2\times h_{\mathrm{cylinder}}, \end{split}

där:

$d_{\mathrm{top}}$ – Övre diameter på frustumen;
$d_{\mathrm{bot}}$ – Nedre diameter på frustumen;
$h_{\mathrm{cone}}$ och $h_{\mathrm{cylinder}}$ – Höjderna på den koniska respektive cylindriska delen av tanken

För att beräkna volymen i en delvis fylld konbotten-tank, adderar du helt enkelt volymen av den fyllda cylinderdelen och den fyllda delen av frustumen, beroende på vätskans nivå. Använd formlerna ovan för varje del.

Att beräkna den totala volymen i en kontopp-tank är exakt samma sak som för en konbotten-tank, men skillnaden kommer när du vill räkna ut den fyllda volymen. I det fallet fylls först den cylindriska delen, och därefter den koniska toppen.

🙋 Har du räknat ut alla volymer i meter och liter, men behöver dem i imperiala enheter istället? Ingen fara! Omni har en smidig lösning: använd vårt verktyg för volymomvandling 🇺🇸 för att snabbt och enkelt konvertera mellan olika volymenheter!

Vanliga frågor

Hur räknar man ut volymen på en vattentank?

Du kan använda Omni Calculators verktyg tankvolym kalkylator eller göra det manuellt så här:

Ta reda på tankens inre radie och höjd.
Kvadrera radien (multiplicera den med sig själv) och multiplicera sedan med pi (≈ 3,1416). Nu har du tankens area.
Multiplicera arean med höjden – resultatet är tankens volym.

Hur räknar man ut motorvolym (slagvolym)?

Bilentusiaster kallar det slagvolym (engine displacement), och du kan räkna ut det så här:

Ta reda på volymen för en av cylindrarna i motorn. Du kan använda Omni Calculators tankvolym kalkylator eller själv mäta cylinderns radie och slaglängd (piston stroke).
Kvadrera radien, multiplicera med π (≈ 3,1416) och därefter med slaglängden. Då får du volymen för en cylinder.
Multiplicera volymen för en cylinder med antalet cylindrar i motorn, det ger dig den totala motorvolymen.

Hur länge räcker vattnet i en tank?

Det beror på hur mycket vatten du har lagrat och hur snabbt det förbrukas. Så här räknar du ut det:

Beräkna volymen på din vattentank med Omni Calculators tankvolym kalkylator. Få resultatet i liter.
Ta reda på hur många liter vatten du förbrukar per dag.
Dividera mängden vatten i tanken med din dagliga förbrukning. Resultatet visar hur många dagar ditt vatten räcker.

Varför föredrar vi cylindriska vattentankar framför fyrkantiga?

Det finns två huvudsakliga skäl till att cylindriska tankar ofta är att föredra framför rektangulära:

Cylindriska tankar tål tryck och påfrestningar bättre än fyrkantiga tankar. Det innebär att tillverkare kan använda mindre material, vilket gör dem både starkare och mer kostnadseffektiva.
Rektangulära tankar är svårare att rengöra, särskilt i hörnen där smuts och bakterier lätt samlas.

Hur stor är volymen på ett oljefat?

218,7 liter. Ett oljefat har en diameter på 0,572 meter och en höjd på 0,851 meter. Sätt in värdena i formeln för volymen av en cylinder:

volym = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 liter