Calculadora de Velocidade Angular

A calculadora de velocidade angular da Omni é uma ferramenta simples e fácil de usar, onde rapidamente você encontrará a resposta para a pergunta: "Como encontrar a velocidade angular?". No texto, você encontrará várias fórmulas de velocidade angular, aprenderá sobre diferentes unidades de velocidade angular e, finalmente, estimará a velocidade angular da Terra!

Você já se perguntou qual é a relação entre a velocidade angular e a frequência angular? Ou onde a velocidade angular é aplicada? Continue lendo para descobrir e se tornar um especialista no campo do movimento circular.

A velocidade angular descreve o movimento de rotação dos corpos. Ela mede a velocidade com que eles se movem em torno de um eixo de rotação. Podemos pensar em dois tipos diferentes de rotações. O primeiro descreve o movimento do centro de massa de um determinado objeto em torno de um ponto específico no espaço, que podemos descrever como uma origem. Alguns exemplos incluem planetas se movendo em torno do Sol ou um carro pegando uma saída na rodovia.

A segunda é sobre a rotação do corpo em torno de seu próprio centro de massa, também conhecido como spin (não confunda com a propriedade quântica das partículas, também chamada de spin). Certamente você já viu um jogador de basquete girando uma bola em seu dedo.

Em geral, podemos dizer que quanto mais rápido o movimento, maior a velocidade angular. Vamos abordar as equações de velocidade angular na próxima seção e veremos alguns exemplos específicos.

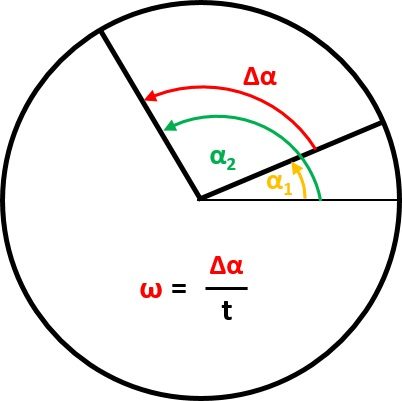
Essa calculadora de velocidade angular usa duas fórmulas de velocidade angular diferentes, dependendo dos parâmetros de entrada que você tiver.

A primeira equação de velocidade angular é análoga à equação de velocidade linear:

onde $\alpha_1$ e $\alpha_2$ são dois valores de ângulos em um círculo, e $\Delta\alpha$ é a diferença entre eles. $t$ é o tempo em que ocorre a mudança de ângulo. Como você pode ver, para a velocidade usual, há uma proporção da mudança de posição em um período, enquanto aqui usamos o ângulo em vez da distância.

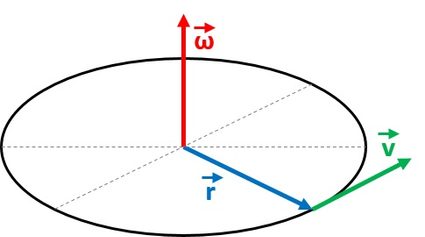
Você pode derivar a segunda fórmula de velocidade angular considerando o produto vetorial entre a velocidade linear e o raio, cuja forma é:

Podemos reescrever essa equação para obter a velocidade angular:

onde todas essas variáveis são vetores, e $|r|$ denota o valor absoluto do raio. Na verdade, a velocidade angular é um pseudovetor, cuja direção é perpendicular ao plano do movimento de rotação.

Há várias unidades de velocidade angular, e as que usamos na nossa calculadora de velocidade angular são mencionadas abaixo:

• rad/s ou radianos por segundo: a definição vem diretamente da primeira fórmula da velocidade angular. Ela informa o tamanho da rotação (ou ângulo) pela qual o corpo se move em um determinado tempo.

• RPM ou revoluções por minuto: a unidade que você encontra com mais frequência em aplicações práticas. Com ela, você pode descrever a velocidade com que uma roda ou um motor gira. Você pode facilmente imaginar a diferença entre 10 e 100 RPM.

• Hz ou hertz: as mesmas unidades usadas para frequência, mas raramente usadas no contexto de velocidade angular. É um pouco semelhante a RPM, dizendo-nos quantas rotações completas são feitas em um determinado tempo. A diferença é que, anteriormente, a unidade básica de tempo era um minuto, e aqui é um segundo.

Naturalmente, todas essas unidades de velocidade angular são convertidas entre si usando as seguintes relações:

1 RMP = 0,10472 rad/s = 0,01667 Hz

Ou o contrário:

1 Hz = 6,283 rad/s = 60 RPM

A frequência angular é definida como:

onde $f$ é a frequência. Além disso, a unidade da frequência angular é rad/s, exatamente a mesma da velocidade angular. Portanto, você pode se perguntar: "Qual é a diferença entre velocidade angular e frequência angular?".

A resposta é relativamente simples. A relação entre a frequência angular e a velocidade angular é análoga àquela entre velocidade escalar e a velocidade. A primeira é uma magnitude da segunda; em outras palavras, a frequência angular é um escalar, enquanto a velocidade angular é um (pseudo)vetor.

Geralmente usamos a frequência angular quando falamos de um movimento harmônico, um exemplo disso é um pêndulo simples. Como você pode imaginar, o movimento não precisa ser representado por uma rotação padrão, simplesmente um movimento que repete periodicamente sua posição. A velocidade angular, no entanto, está estritamente ligada ao movimento em torno de algum ponto. Portanto, podemos dizer que a frequência angular é uma quantidade mais geral, e podemos usá-la para descrever uma ampla gama de problemas físicos. Por outro lado, a velocidade angular inclui apenas o movimento rotacional.

Que tal usarmos nossa calculadora de velocidade angular? Vamos estimar a velocidade angular da Terra! Em primeiro lugar, consideramos a velocidade de rotação. Sabemos que a Terra está fazendo uma rotação completa, em relação às estrelas distantes, em cerca de 23 h 56 min 4 s, que é aproximadamente 23,934 h. A rotação completa é o ângulo 2π rad, portanto, a velocidade angular resultante é:

ou $7{,}292 \times 10^{-5}\ \rm rad/s$ (usando notação científica).

Agora que sabemos a velocidade angular de rotação da Terra, podemos avaliar sua velocidade linearmente no equador. Para fazer isso, precisamos do raio da Terra, que é aproximadamente 6.371 km. A única coisa que precisamos fazer é inserir os valores na segunda fórmula da velocidade angular:

Para obter a velocidade linear em relação ao centro da Terra, tudo o que você precisa fazer é multiplicar este resultado pelo cosseno da latitude da sua cidade.

A propósito, você já se perguntou por que os foguetes geralmente são lançados de bases de lançamento espacial localizados perto do equador e não dos polos? Esta localização resulta em impulso de aproximadamente 500 m/s na ignição, sendo este uma fração considerável da sua velocidade final. Portanto, ao mover o ponto de partida para o mais próximo possível do equador, você reduz a quantidade de combustível necessária para acelerar o foguete.

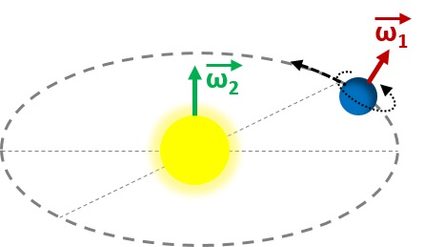
Depois disso, podemos perguntar mais uma vez como encontrar a velocidade angular da Terra, mas dessa vez a velocidade orbital. Todos os cálculos são análogos, mas temos que mudar o tempo de 23,943 h para um ano, que é cerca de 365,25 dias. A mudança de ângulo é a mesma, uma revolução completa.

e a velocidade linear da Terra em relação ao Sol (para o raio médio $\small 1{,}496\!\times\!10^8\ \rm km$) é:

Estamos nos movendo muito rápido, não é mesmo?

Vários parâmetros físicos estão relacionadas à velocidade angular, alguns dos quais estão listados abaixo:

1. Aceleração angular: descreve como a velocidade angular muda com o tempo. Quanto maior for a diferença entre as velocidades angulares, maior será o valor da aceleração angular. Você pode verificar como ela funciona na prática com nossa calculadora de aceleração angular 🇺🇸.

2. Energia cinética rotacional : mede a energia em um movimento circular. Assim como a energia cinética, a dependência da velocidade (angular) é quadrática.

3. Força centrípeta - É a força que mantém você girando ou rodando; em movimento circular. Em um carro girando, os pneus estão exercendo essa força. A tendência de manter você em linha reta (primeira lei de Netown) é chamada de inércia, às vezes chamada de força centrífuga, embora não seja uma força real.

4. Efeito Coriolis : faz com que os objetos girem se estiverem em um corpo em rotação (por exemplo, na Terra) em vez de se moverem em uma reta.

5. Sistema de polias : não se trata de um parâmetro físico, precisamente falando, mas é um dispositivo interessante que tem tudo a ver com velocidade angular. O sistema mais simples consiste em duas polias, geralmente com circunferências ou raios diferentes. Uma correia as conecta, de modo que suas velocidades lineares são idênticas, mas como são de tamanhos diferentes, suas velocidades angulares mudam proporcionalmente.

   Sabendo disso, e considerando um motor com velocidade de rotação bem definida, podemos determinar a velocidade angular do elemento de saída com boa precisão simplesmente ajustando o seu tamanho.

Algumas regras fundamentais nos informam sobre as quantidades conservadas em sistemas isolados. As mais conhecidas são a conservação da energia e a conservação do momento. Junto com elas, há também a conservação do momento angular. Se pensarmos em dois valores de momentos, podemos escrever a regra como:

em que $I_1$ e $I_2$ são os momentos de inércia de massa inicial e final, respectivamente, que descrevem a distribuição de massa em relação aos seus respectivos eixos de rotação.

Podemos ver que se o momento de inércia aumenta, a velocidade angular diminui e vice-versa. Então, quais são as consequências desse fenômeno?

Vamos imaginar que você é um patinador artístico. Ao girar, você possui alguma velocidade angular. Se você estiver com os braços bem abertos, o momento de inércia da massa é relativamente grande. Então, você move seus braços para perto do resto do corpo. Como consequência, seu momento de inércia diminui, portanto, como o momento angular geral precisa ser conservado, sua velocidade angular aumenta, o que significa que você girará mais rápido! Isso não é mágica, é apenas física!

Se não puder/não gostar de patinar, você pode tentar verificar a regra com uma cadeira giratória comum. Mas lembre-se: segurança em primeiro lugar! Certifique-se de que você tem espaço suficiente para fazer esse experimento. Depois disso, basta começar a girar e ver como a velocidade angular muda quando você move os braços para frente e para trás. Além disso, você pode aumentar o efeito usando alguns halteres. Como resultado, você pode combinar exercício e diversão em um único experimento!