Kalkulator złotego podziału

Kalkulator złotego podziału obliczy długość części, na które musisz podzielić odcinek, aby uzyskać złotą proporcję. Zanim przejdziemy do samego obliczania złotej proporcji, omówmy, na czym ona polega. W poniższym artykule znajdziesz całą potrzebną wiedzę!

Możesz również odwiedzić nasz kalkulator proporcji 🇺🇸, aby zapoznać się z samym pojęciem proporcji.

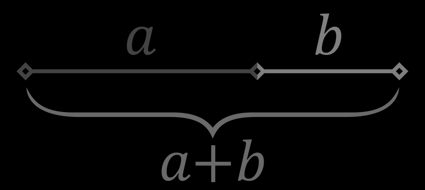
Złoty podział (zwany złotą proporcją) powstaje, gdy podzielimy odcinek na dwie części tak, aby stosunek dłuższej z nich do krótszej był taki sam jak stosunek całego odcinka do dłuższej części. Jeśli długość dłuższej części oznaczymy przez $a$, zaś krótszej przez $b$, to wzór złotej proporcji wygląda następująco:

Aby obliczyć wartość złotej proporcji, trzeba z powyższego równania wyliczyć $a/b$. Wygodnie jest przekształcić je do postaci

Ostatecznie pozostaje nam tylko rozwiązać równanie kwadratowe $x^2-x-1=0$. Robiąc to standardowymi metodami, odkryjemy, że wartość złotej proporcji wynosi $\frac 12 (1+\sqrt{5})$, co daje w przybliżeniu $1,\!61803398875...$. Liczbę tę najczęściej oznaczamy grecką literą $\phi$.

Wiemy już, czym jest złota proporcja i jak obliczyć jej wartość. Czas wyjaśnić, jak możesz sprawdzić, czy dwie długości zachowują boską proporcję.

Oto instrukcja krok po kroku:

1. Wyznacz długość dłuższego odcinka i oznacz go przez a.
2. Wyznacz długość krótszego odcinka i oznacz go przez b.
3. Oblicz a/b.
4. Jeśli proporcja jest (w przybliżeniu) równa 1,618, to twoje odcinki są w złotej proporcji!

Aby wykonać to zadanie, możesz również użyć kalkulatora złotego podziału Omni. Każdy kalkulator stosunków będzie pomocny, ale nasz kalkulator złotej proporcji został stworzony specjalnie do tego, więc nie znajdziesz lepszego narzędzia!

Kalkulator złotej proporcji Omni jest nadzwyczaj przyjazny i prosty w użyciu: znajdziesz w nim trzy pola, odpowiadające trzy długościom, które pojawiają się we wzorze na złotą proporcję. Wystarczy, że wpiszesz jedną z nich, aby pozostałe dwie zostały obliczone automatycznie. Czyż nie jest to wspaniałe?

Złoty prostokąt to prostokąt, w którym długości boków są ze sobą w złotej proporcji, tzn. stosunek długości dłuższego do krótszego boku wynosi $1,\!618$. Prostokąt ten jest często wykorzystywany w sztuce, gdyż panuje przekonanie, że jest on szczególnie przyjemny dla ludzkiego oka. Jeśli nie chcesz obliczać ręcznie długości jego boków, skorzystaj z kalkulator złotego prostokąta 🇺🇸.

Matematyczne i estetyczne właściwości złotej proporcji sprawiły, że zawsze miała on szczególne znaczenie w nauce i sztuce. W matematyce:

• Złoty prostokąt może być podzielony na dwa mniejsze złote prostokąty (przy podziale zachowuje on swoje proporcje).
• Złota proporcja ma tajemnicze związki z liczbą 5, która pojawia się w złotej liczbie φ = (1 + √5)/2 oraz w pięciokącie (jako stosunek przekątnej do boku).

W sztuce złotą proporcję wykorzystywał w swoich pracach m.in. Dalí.

Wiele źródeł, zarówno historycznych jak i współczesnych, twierdzi, że złota proporcja jest wszechobecna w naturze. Niektóre przykłady to:

• wzór wzrostu liści;
• geometryczne powierzchnie niektórych warzyw i muszli;
• proporcje kości niektórych zwierząt.

Jednakże, o ile nie da się zaprzeczyć obecności geometrycznych wzorców w przyrodzie, nie można też ponad wszelką wątpliwość stwierdzić, czy w powyższych przykładach rzeczywiście występuje złota proporcja: czasami mamy bowiem do czynienia wyłącznie z (lepszym lub gorszym) przybliżeniem.