Kalkulator ciągu geometrycznego

Q: Jak znaleźć sumę n wyrazów ciągu geometrycznego?

Aby znaleźć sumę n początkowych wyrazów ciągu geometrycznego: Weź iloraz ciągu r podniesiony do potęgi n . Odejmij rⁿ od 1 . Podziel wynik przez (1 - r) . Pomnóż wynik przez pierwszy wyraz, a₁ . Read more

Q: Jak znaleźć n-ty wyraz ciągu geometrycznego?

Aby znaleźć n-ty wyraz ciągu geometrycznego: Oblicz iloraz podniesiony do potęgi (n-1) . Pomnóż otrzymany wynik przez pierwszy wyraz ciągu, a . Read more

Q: Jak obliczyć iloraz ciągu geometrycznego?

Aby obliczyć iloraz ciągu geometrycznego, podziel dowolne dwa kolejne wyrazy ciągu: kolejny przez poprzedni. Read more

Created by Álvaro Díez and Anna Szczepanek, PhD

Reviewed by Bogna Szyk and Jack Bowater

Translated by Anna Szczepanek, PhD and Dominik Czernia, PhD

Last updated: Jan 18, 2024

Table of contents:

Za pomocą Omni kalkulatora ciągu geometrycznego obliczysz wszystko, co tylko dotyczy tego typu ciągów! Nasz kalkulator pomoże ci zrozumieć definicję ciągu geometrycznego i poznasz dzięki niemu odpowiedź na pytanie, czym faktycznie jest ciąg geometryczny. Wyjaśnimy ci też różnicę między dwoma popularnymi równaniami ciągu geometrycznego: wzorem jawnym i rekurencyjnym. Wykorzystanie tych wzorów omówimy na kilku ciekawych przykładach ciągów geometrycznych.

Nasze narzędzie ma zaimplementowaną funkcję „sumowania szeregu geometrycznego”, która obliczy sumę wybranych wyrazów twojego ciągu geometrycznego.

Definicja ciągu geometrycznego

Definicja ciągu geometrycznego mówi, że jest to zbiór liczb, w którym wszystkie oprócz pierwszej są otrzymywane przez pomnożenie poprzedniej liczby przez pewną stałą, ale niezerową wartość zwaną ilorazem ciągu. Nie martw się jeśli, czytając tę definicję, masz trudności ze zrozumieniem, czym jest ciąg geometryczny. W dalszej części wyjaśnimy w prostych słowach, co ta definicja oznacza, a także przyjrzymy się rekurencyjnemu i jawnemu wzorowi na ciąg geometryczny.

Zauważmy, że ciąg geometryczny ma sporo wspólnego z największym wspólnym dzielnikiem (NWD) i najmniejszą wspólną wielokrotnością (NWW), ponieważ wszystkie liczby wybrane z ciągu geometrycznego mają wspólny NWD i NWW, o ile pierwszy wyraz ciągu i jego iloraz są liczbami całkowitymi.

Mówiąc bardziej precyzyjnie, NWD (zob. Omni kalkulator NWD) tych liczb będzie równe najmniejszej z nich, zaś NWW największej z nich. Na przykład, w zbiorze 3, 6, 12, 24, 48 NWD wynosi 3, a NWW to 48. Ale jeśli weźmiemy pod uwagę tylko liczby 6, 12, 24, to NWD wyniesie 6, a NWW 24.

Czym jest postęp geometryczny?

Zobaczmy teraz, czym jest ciąg geometryczny z punktu widzenia laika. Otóż ciąg geometryczny to zbiór liczb, które są powiązane wspólnym stosunkiem, o którym wspomnieliśmy wcześniej. Ten wspólny stosunek (iloraz ciągu) oraz początkowy wyraz to cechy całkowicie definiujące dany ciąg. Zobaczymy później, jak za pomocą tych dwóch liczb można uzyskać jawny wzór na ciąg geometryczny lub równoważny wzór rekurencyjny na ciąg geometryczny.

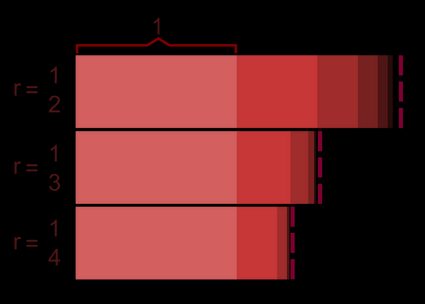
Przykłady ciągów geometrycznych o ilorazie 1/2, 1/3, 1/4 oraz wyrazie początkowym równym 1. — Przykłady ciągów geometrycznych o różnych proporcjach

Teraz skonstruujmy prosty ciąg geometryczny, używając konkretnych wartości dla tych dwóch parametrów. Aby uprościć sprawę, przyjmiemy, że początkowy wyraz to $1$ , a iloraz ustalmy na $2$ . W tym przypadku pierwszy wyraz wyniesie $a_1 = 1$ , drugi $a_2 = a_1 \cdot 2 = 2$ , trzeci $a_3 = a_2 \cdot 2 = 4$ itd. Wówczas n-ty wyraz ciągu wynosiłby:

a_{n} = 1 \cdot 2^{{n}-1}

gdzie $n$ jest liczbą naturalną opisującą pozycję danego wyrażenia w ciągu.

Jak widać, proporcja dowolnych dwóch kolejnych wyrazów ciągu — zdefiniowana tak samo jak w naszym kalkulatorze stosunków 🇺🇸 — jest stała i równa wspólnemu stosunkowi.

Powszechnym sposobem zapisu ciągu geometrycznego jest wypisanie kilku pierwszych wyrazów. Pozwala to obliczyć dowolną inną liczbę w ciągu; w naszym przykładzie zapisalibyśmy ciąg jako:

1, 2, 4, 8, ...

Istnieją jednak bardziej matematycznie wysublimowane sposoby dostarczenia tych samych informacji. Są to tak zwany jawny i rekurencyjny wzór na ciąg geometryczny. Teraz gdy rozumiemy już, czym jest ciąg geometryczny, możemy zagłębić się w tematykę tych wzorów i poznać sposoby przekazywania tych samych informacji za pomocą mniejszej liczby słów.

Rekursywny a jawny wzór na ciąg geometryczny

Istnieją dwa sposoby, na jakie można matematycznie przedstawić ciąg geometryczny za pomocą tylko jednego wzoru: jawny wzór na ciąg geometryczny i rekurencyjny wzór na ciąg geometryczny. Pierwszy z nich to ten, który już widzieliśmy w naszym przykładzie ciągu geometrycznego. Mówiąc bardziej precyzyjnie, widzieliśmy jawny wzór dla omawianego przykładu, ale można bardzo podobnie napisać wzór dla dowolnego ciągu geometrycznego — wystarczy zastąpić konkretne wartości symbolami: wyrazu początkowego $a$ i stosunku $r$ . Ogólny wzór na n-ty wyraz to:

a_{n} = ar^{{n}-1}, n \in \mathbb N

gdzie $n \in \mathbb N$ oznacza, że $n = 1, 2, 3, \ldots$ . Wzór rekurencyjny dla ciągów geometrycznych przekazuje wszystkie potrzebne informacje o ciągu geometrycznym: wyraz początkowy i sposób uzyskania dowolnego wyrazu z pierwszego.

Istnieje inny sposób na przekazanie tych samych informacji za pomocą innego typu wzoru, a mianowicie wzoru rekurencyjnego dla ciągu geometrycznego. Składa się on z dwóch części: pierwsza wyjaśnia, jak dostać się z poprzedniego wyrazu ciągu do kolejnego wyrazu za pomocą proporcji. W konsekwencji wiemy, jak dostać się z dowolnego wyrazu ciągu do dowolnego innego. Ale samo to nie wystarcza do skonstruowania ciągu geometrycznego, bo nie znamy wyrazu początkowego. Jest to druga część wzoru: pierwszy wyraz (lub którykolwiek inny!). Zobaczmy, jak wygląda ta formuła rekurencyjna:

\begin{align*} a_{n} &= a_{n-1} r \\ a_{i} &= x \end{align*}

Pierwsze równanie zachodzi dla każdego $n \in \mathbb N$ , zaś w drugim istnieje $i$ , oznaczające dowolną liczbę naturalną, dla której wiemy, że $i$ -ty wyraz ciągu ma wartość $x$ .

Jak korzystać z kalkulatora ciągu geometrycznego?

Gdy już wiesz, czym jest ciąg geometryczny i jak zapisać go zarówno w formule rekurencyjnej, jak i jawnej, nadszedł czas, aby zastosować swoją wiedzę i przeliczyć kilka przykładów! Dzięki naszemu narzędziu możesz obliczyć wszystkie właściwości ciągów geometrycznych, takie jak iloraz, pierwszy wyraz, n-ty wyraz, itp. Oto krótki opis struktury kalkulatora:

Najpierw powiedz nam, co wiesz o swoim ciągu, wybierając wartość zmiennej Typ:
- wspólny współczynnik i pierwszy wyraz ciągu;
- wspólny współczynnik i jakiś n-ty wyraz; lub
- dowolne dwa wyrazy;
Wprowadź swoje dane. Na tej podstawie kalkulator wyznaczy twój ciąg geometryczny.
Domyślnie kalkulator pokaże ci pierwszych pięć wyrazów tego ciągu, ale możesz to łatwo zmienić i wyświetlić te wyrazy, których potrzebujesz.

Nasze narzędzie może również obliczyć sumę ciągu geometrycznego: wszystkich jego wyrazów (nieskończenie wielu!) lub też skończonego fragmentu ciągu. W tym drugim przypadku wystarczy wprowadzić początkowy i końcowy punkt sumy i cieszyć się wynikiem. Jak dowiesz się w kolejnych sekcjach, suma wszystkich wyrazów może nie istnieć!

Wzory na ciąg geometryczny: suma ciągu geometrycznego

Do tej pory traktowaliśmy ciągi geometrycznych jako zbiory liczb. Interesujące wyniki można uzyskać, gdy postanowimy zsumować wyrazy ciągu geometrycznego. Gdy mamy skończony podzbiór ciągu, proces sumowania jest bardzo prosty. Można to nawet zrobić ręcznie.

Będziemy jednak bardziej wydajni, jeśli użyjemy wzoru na sumę ciągu geometrycznego. Aby to zrobić, użyjemy matematycznego znaku sumowania $\Sigma$ , co będzie oznaczało sumowanie wszystkich wyrazów ciągu. Na przykład, jeśli mamy ciąg geometryczny o wyrazach $a_n$ i nazwiemy sumę ciągu geometrycznego $S$ , związek między nimi będzie następujący:

\scriptsize S = \sum_{n=1}^m a_{n} = a_{1} + a_{2} + a_{3} + ... + a_m

jeśli chcemy zsumować pierwsze $m$ wyrazów, lub:

\scriptsize S = \sum_{n=1}^\infty a_{n} = a_{1} + a_{2} + a_{3} + \ldots

jeśli chcemy zsumować wszystkie wyrazy.

Niestety, nadal pozostaje problem faktycznego obliczenia sumy szeregu geometrycznego. Zawsze możesz użyć naszego kalkulatora jako kalkulatora sumy szeregu geometrycznego, ale byłoby znacznie lepiej, gdybyśmy przed użyciem jakiegokolwiek kalkulatora zrozumieli, jak obliczyć tę sumę ręcznie. Istnieje sztuczka, która może znacznie ułatwić nam pracę i która polega na zastosowaniu równania ciągu geometrycznego w następujący sposób:

\scriptsize \begin{align*} S &= \sum_{n=1}^m a_{n} = \\ &= a_{1} + a_{1}r + a_{1}r^2 + ... + a_{1}r^{m-1} \end{align*}

Teraz pomnożymy obie strony przez $(1-r)$ :

\scriptsize \begin{align*} \scriptsize S (1 - r) &= (1 - r) (a_1 + a_1r + a_1r^2 + \ldots +\ a_1r^{m-1}) \\[1.5em] S(1-r) &= a_1 + a_1r + ... + a_1r^{m-1} \\ &\ -(a_1r + a_1r^2 + \ldots + a_1r^{m}) \\[.5em] &= a_1 - a_1r^{m} \end{align*}

\scriptsize S = \sum_{n=1}^m a_{n} = a_1 - a_1 \frac{r^{m}}{1-r} = a_1 \frac{1-r^m}{1-r}

Wzór ten można łatwo wyprowadzić samodzielnie i stanowi on podstawowy wzór szeregu geometrycznego, gdy liczba wyrazów w szeregu jest skończona.

Możemy rozważać też nieskończoną liczbę wyrazów szeregu i nadal być w stanie obliczyć całkowitą sumę wszystkich wyrazów! Jak działa ta magia? Omówimy to w kolejnym paragrafie.

Użycie wzoru ciągu geometrycznego do obliczenia sumy nieskończonej

Po wyprowadzeniu wzoru na sumę ciągu geometrycznego dla skończonej liczby wyrazów naturalne jest pytanie (przynajmniej dla matematyków): jak mogę obliczyć nieskończoną sumę ciągu geometrycznego? Intuicyjnie może się to wydawać bardzo trudne lub wręcz niemożliwe, ale zaraz zobaczymy, jak obliczyć tę wartość w kilku prostych krokach. W tym celu musimy wprowadzić pojęcie granicy. Jest to pojęcie matematyczne, dzięki któremu możemy zrozumieć, co dzieje się w nieskończoności. Można go również użyć do próby poprawnego matematycznie zdefiniowania wyrażeń, które zwykle są niezdefiniowane, takich jak „zero podzielone przez zero” lub „zero do potęgi zero”.

Granice ciągów to dość złożony temat, który wykracza poza zakres tego kalkulatora. Aby niepotrzebnie nie komplikować zagadnienia, zdecydowaliśmy się tylko o tym wspomnieć i nie wchodzić w szczegóły dotyczące obliczania granic. Jeśli chcesz, możesz znaleźć doskonałe artykuły na temat granic, np. na Wikipedii.

Nawet jeśli nie masz ochoty sprawdzać, czym są granice, nadal możesz obliczyć nieskończoną sumę szeregu geometrycznego za pomocą naszego kalkulatora. Jedyną rzeczą, którą musisz wiedzieć, jest to, że nie każdy szereg geometryczny ma sumę. Warunki, które musi spełnić szereg geometryczny, aby jego suma była liczbą (matematycy nazywają to zbieżnością), są w zasadzie proste. Wyjaśnimy je w poniższej sekcji.

Uwagi dotyczące korzystania z kalkulatora jako kalkulatora szeregów geometrycznych

Jeśli chodzi o szeregi (zarówno w przypadku ciągów geometrycznych, jak i arytmetycznych), są one często grupowane w dwóch różnych kategoriach, w zależności od tego, czy ich nieskończona suma jest skończona (szereg zbieżny), czy nieskończona / nieokreślona (szereg rozbieżny). Najlepszym sposobem, aby dowiedzieć się, czy szereg jest zbieżny, czy nie, jest zbadanie granicy sum częściowych. Oprócz tego istnieją pewne sztuczki, które pozwalają nam szybko odróżnić szeregi zbieżne od rozbieżnych bez konieczności wykonywania wszystkich obliczeń. Sztuczki te obejmują: spojrzenie na początkowy i n-ty (ogólny) wyraz szeregu, stosunek kolejnych wyrazów lub porównanie szeregu z innymi szeregami.

Wizualizacja sumy ciągu geometrycznego o początkowym wyrazie 1 i ilorazie 1/2 w postaci pola prostokąta podzielonego na coraz mniejsze prostokąty. — Wizualizacja sumy ciągu geometrycznego

Aby szereg był zbieżny, wyraz ogólny $a_n$ musi zmniejszać się wraz ze wzrostem wartości $n$ . Jeśli $a_n$ maleje, nie możemy zagwarantować, że szereg będzie zbieżny, ale jeśli $a_n$ nie maleje (tzn. jest stały lub rośnie) wraz ze wzrostem $n$ , możemy z całą pewnością powiedzieć, że szereg będzie rozbieżny. Jeśli nie jesteśmy pewni, czy $a_n$ maleje, możemy spojrzeć na początkowy wyraz i iloraz, a nawet obliczyć niektóre z pierwszych wyrazów. Da nam to wyobrażenie o tym, jak zmienia się $a_n$ .

Drugą opcją, jaką mamy, jest porównanie naszego nieujemnego szeregu z nieujemnym szeregiem, o którym wiemy na pewno, że jest zbieżny (lub wiemy, że jest rozbieżny). Mówiąc ogólnie, jeśli każdy wyraz $a_n$ badanego szeregu jest mniejszy lub równy niż odpowiadający mu wyraz szeregu, o którym wiemy, że jest zbieżny, to nasz szereg również będzie zbieżny. I odwrotnie, jeśli każdy wyraz naszego szeregu jest większy niż odpowiadający mu wyraz szeregu, o którym wiemy na pewno, że jest rozbieżny, to nasz szereg będzie rozbieżny. W pozostałych przypadkach (większy niż zbieżny lub mniejszy niż rozbieżny) nie możemy nic powiedzieć o naszym szeregu i jesteśmy zmuszeni znaleźć inny szereg do porównania lub użyć innej metody.

Kryteria te mają zastosowanie do ciągów arytmetycznych i geometrycznych. W rzeczywistości są one ze sobą ściśle powiązane i oba ciągi można połączyć za pomocą operacji potęgowania i logarytmowania.

Paradoks Zenona i inne przykłady ciągów geometrycznych

Widzieliśmy już przykład ciągu geometrycznego w postaci ciągu potęg dwójki 🇺🇸. Jest to bardzo ważny ciąg ze względu na komputery i stosowaną w nich binarną reprezentację danych. W szeregu tym możemy znaleźć takie wartości jak maksymalna dozwolona liczba w komputerze (różni się ona w zależności od typu zmiennej, której używamy w programowaniu), liczba bajtów w gigabajcie lub liczba sekund do końca czasu UNIX (zarówno oryginalne, jak i poprawione wartości).

Poza potęgami dwójki możemy rozważać każdy inny szereg potęgowy — wystarczy po prostu zastąpić $r = 2$ inną wartością, która nas interesuje. Ciągi potęgowe są powszechnie używane i znane i mogą być wyrażone za pomocą wygodnego wzoru. Zaraz pokażemy ci inne ważne i ciekawe szeregi geometryczne, takie jak szereg naprzemienny lub oszałamiający paradoks Zenona z Elei.

Zacznijmy od paradoksu Zenona, w szczególności od tak zwanego paradoksu dychotomii. Paradoks ten jest w swej istocie zagadką matematyczną w postaci nieskończonego ciągu geometrycznego. Zenon był greckim filozofem poprzedzającym Sokratesa. Opracował argument, który dowodził, że jakikolwiek ruch jest niemożliwy i nigdy nie powinien mieć miejsca w prawdziwym życiu. Pomysł polega na podzieleniu odległości między punktem początkowym (A) a punktem końcowym (B) na pół. Pokonujemy pierwszą połowę i pozostały dystans dzielimy ponownie na pół... Proces ten można powtarzać dowolną ilość razy, co oznacza, że zawsze pozostanie nam jakiś dystans do punktu B.

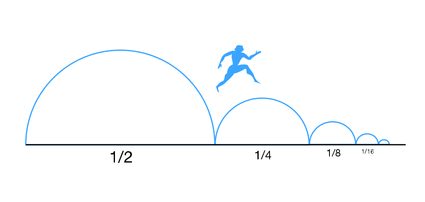
Wizualizacja paradoksu dychotomii Zenona. Postać greckiego sprintera za każdym razem przebiega 1/2 długości poprzedniego odcinka, przez co nigdy nie ukończy biegu. — Wizualizacja paradoksu dychotomii Zenona.

Paradoks Zenona zakłada, że skoro mamy nieskończoną liczbę połówek do przejścia, to będziemy potrzebować nieskończonej ilości czasu na podróż z punktu A do punktu B. Jednak, jak wiemy z naszego codziennego doświadczenia, nie jest to prawdą i zawsze możemy dotrzeć z punktu A do punktu B w skończonym czasie (może z wyjątkiem osób, które zawsze są spóźnione). Rozwiązanie tego pozornego paradoksu można znaleźć za pomocą matematyki.

Jeśli wyrazimy czas potrzebny na dotarcie z punktu A do punktu B (nazwijmy go na razie $t$ ) w postaci szeregu geometrycznego, otrzymamy szereg zdefiniowany przez: $a_1 = t/2$ z ilorazem $r = 1/2$ . Tak więc przejście pierwszej połowy zajęłoby $t/2$ , następnie pokonalibyśmy połowę pozostałego dystansu w $t/4$ , następnie $t/8$ , itd... Jeśli teraz obliczymy nieskończoną sumę szeregu geometrycznego, okaże się, że:

\scriptsize\begin{align*} S &= \sum_{n=1}^\infty aₙ = \frac{t}{2} + \frac{t}{4} + ... \\[1em] &= t \cdot \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...\right) = t \cdot 1 = t \end{align*}

Jest to matematyczny dowód na to, że możemy dostać się z punktu A do punktu B w skończonym czasie ( $t$ w tym przypadku).

Na zakończenie i na wypadek, gdyby paradoks Zenona nie był wystarczająco oszałamiającym doświadczeniem, wspomnimy jeszcze o naprzemiennym szeregu geometrycznym jedności.

Szereg ten zaczyna się od $a_1 = 1$ i ma iloraz $r = -1$ , co tworzy szereg w postaci:

\scriptsize S = \sum_{n=1}^\infty aₙ = 1 - 1 + 1 - 1 + ...

Szereg ten nie jest zbieżny, ponieważ suma częściowa zależy od tego, czy bierzemy parzystą ( $S = 0$ ) czy nieparzystą ( $S = 1$ ) liczbę wyrazów. Istnieje jednak sztuczka, dzięki której możemy „obliczyć” sumę tego szeregu. Sama sztuczka jest bardzo prosta, ale opiera się na nieco szemranych argumentach, więc ryzykujesz wpadnięcie w poważne kłopoty jeśli kiedykolwiek pokażesz to matematykowi (podobną reakcję wywołałaby rozmowa o słynnej hipotezie Collatza). Tyle ostrzeżeń. Zobaczmy „rozwiązanie”:

\scriptsize S = 1 - 1 + 1 - 1 + ...

Mnożymy obie strony przez $-1$ :

\scriptsize\begin{align*} -S &= -1 + 1 - 1 + 1 - ... \\[1em] &= -1 + (1 - 1 + 1 - 1 + ...) \\[1em] &= -1 + S \end{align*}

Jeśli rozwiążemy wzór i wyznaczymy $S$ to:

\scriptsize -S - S = -1 → 2S = 1 → S = 1/2

Teraz możesz iść i pochwalić się znajomym (o ile nie są matematykami).

FAQ

Czym jest ciąg geometryczny?

Ciąg geometryczny to ciąg liczbowy, w którym kolejny wyraz jest otrzymywany przez pomnożenie poprzedniego wyrazu przez pewną ustaloną liczbę, zwaną ilorazem ciągu.

Jak znaleźć sumę n wyrazów ciągu geometrycznego?

Aby znaleźć sumę n początkowych wyrazów ciągu geometrycznego:

Weź iloraz ciągu r podniesiony do potęgi n.
Odejmij rⁿ od 1.
Podziel wynik przez (1 - r).
Pomnóż wynik przez pierwszy wyraz, a₁.

Jak znaleźć n-ty wyraz ciągu geometrycznego?

Aby znaleźć n-ty wyraz ciągu geometrycznego:

Oblicz iloraz podniesiony do potęgi (n-1).
Pomnóż otrzymany wynik przez pierwszy wyraz ciągu, a.

Jak obliczyć iloraz ciągu geometrycznego?

Aby obliczyć iloraz ciągu geometrycznego, podziel dowolne dwa kolejne wyrazy ciągu: kolejny przez poprzedni.

Álvaro Díez and Anna Szczepanek, PhD

Formula to find the n-th term of the geometric sequence:

Type

Common ratio r

a₁

Here's your sequence

Starting from term no.

Up to term no.

a₁ =

a₂ =

a₃ =

a₄ =

a₅ =

Summing the sequence

Find

a₁ + a₂ + a₃ + ... =

To increase the precision of calculations, go to the advanced mode.

Arithmetic sequenceCollatz conjectureConvolution… 7 more