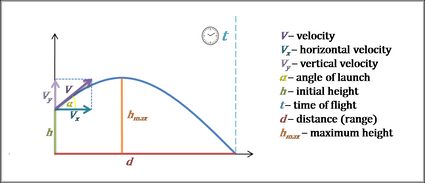
Kalkulator rzutu ukośnego

Omni kalkulator rzutu ukośnego to narzędzie, które pomaga objaśnić ruch obiektów w jednorodnym polu grawitacyjnym. Można w nim znaleźć czas lotu, jak również składowe prędkości, zasięg oraz maksymalną wysokość lotu. Jeśli chcesz zrozumieć, czym jest rzut ukośny, zapoznać się z jego definicją i wyznaczyć wyżej wymienione wartości za pomocą równań rzutu parabolicznego, to wszystkie te informacje znajdziesz w dalszej części artykułu.

Wolisz oglądać niż czytać? Dowiedz się wszystkiego w 90 sekund dzięki filmowi, który zrobiliśmy dla ciebie:

Wyobraźmy sobie łucznika posyłającego w powietrze strzałę. Zaczyna ona poruszać się w górę i do przodu, pod pewnym nachyleniem do ziemi. Im dalej leci, tym wolniejsze jest jej wznoszenie, aż w końcu zaczyna opadać, poruszając się teraz w dół i do przodu, by ostatecznie uderzyć w podłoże. Gdybyśmy mogli prześledzić jej drogę, byłaby to trajektoria w kształcie paraboli. Każdy obiekt poruszający się w taki sposób możemy opisać przy pomocy rzutu ukośnego. Przy okazji, mamy kalkulator prędkości strzał, który jest poświęcony wyłącznie ruchowi strzał — spróbuj!

Na obiekt w ruchu ukośnym działa tylko jedna siła — siła grawitacji. Opór powietrza jest zawsze pomijany. Podobnie jak w przypadku spadku swobodnego na diagramie sił narysujemy tylko jeden wektor w dół i oznaczymy go jako „grawitacja”. Gdyby na ciało działały jakiekolwiek inne siły, to nie byłby to klasyczny rzut ukośny.

Ruch obiektu w rzucie ukośnym jest całkiem logiczny. Załóżmy, że znasz prędkość początkową przedmiotu $V$, kąt wyrzutu $\alpha$ i wysokość startową $h$. Prześledźmy jakie korki wykonuje nasz kalkulator rzutu ukośnego, aby znaleźć wszystkie pozostałe parametry:

1. Oblicz składowe prędkości.

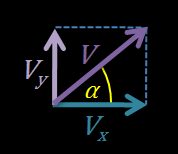
• Składowa pozioma prędkości $V_\mathrm x$ jest równa $V \cos\alpha$.
• Składowa pionowa prędkości $V_\mathrm y$ jest równa $V \sin\alpha$.
• Trzy wektory — $V$, $V_\mathrm x$ i $V_\mathrm y$ tworzą trójkąt prostokątny.

Jeżeli składowa pionowa prędkości wynosi 0, to mamy do czynienia z przypadkiem rzutu poziomego. Jeśli dodatkowo α = 90°, to jest to przypadek swobodnego spadania. Oba przypadki są szczegółowo opisane odpowiednio w kalkulatorze rzutu poziomego 🇺🇸 i kalkulatorze spadku swobodnego.

2. Zapisz równania ruchu.

Odległość i wysokość:

• Odległość w poziomie można wyrazić wzorem $x = V_\mathrm x t$, gdzie $t$ to czas.
• Wysokość od ziemi opisuje wzór $y = h + V_\mathrm{y0} t - g t^2 / 2$, gdzie $g$ to przyspieszenie grawitacyjne, a $V_\mathrm{y0}$ to początkowa pionowa składowa prędkości.

Prędkość:

• Prędkość pozioma jest równa $V_\mathrm x$.
• Prędkość pionową możemy wyrazić wzorem $V_\mathrm y = V_\mathrm{y0} - g t$.

Przyspieszenie:

• Przyspieszenie poziome jest równe 0.
• Przyspieszenie pionowe jest równe $-g$ (ponieważ na pocisk działa tylko grawitacja).

3. Oblicz czas lotu.

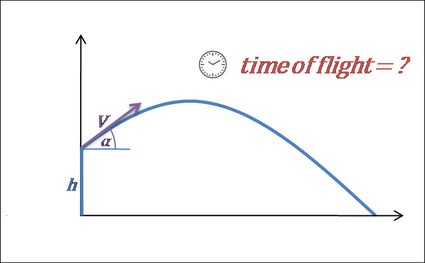
• Lot kończy się, gdy pocisk uderzy w ziemię. Możemy powiedzieć, że dzieje się tak, gdy jego wysokość jest równa 0. W przypadku, gdy wysokość początkowa wynosi 0, wzór można zapisać jako: $V_\mathrm{y0} t - g t^2 / 2 = 0$. Następnie z tego równania dowiadujemy się, że czas lotu wynosi:

• Jeśli jednak rzucamy obiektem z jakiejś niezerowej wysokości, to wzór nie jest już tak prosty jak poprzednio i otrzymujemy równanie kwadratowe: $h + V_\mathrm{y0} t - g t^2 / 2 = 0$. Po rozwiązaniu tego równania otrzymujemy:

4. Oblicz zasięg pocisku.

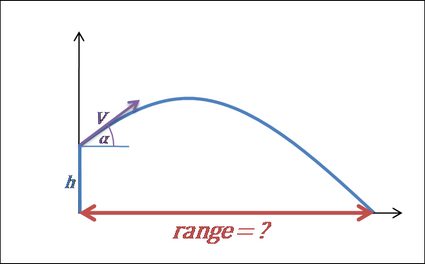
• Zasięg pocisku to całkowita odległość pozioma przebyta w czasie lotu. I znów, jeśli wystrzeliwujemy obiekt z ziemi (wysokość początkowa = 0), to wzór możemy zapisać jako $R = V_\mathrm x t = V_\mathrm x \cdot 2 \cdot V_\mathrm{y0} / g$. Możemy też przekształcić to wyrażenie jako: $R = V^2_0 \sin(2\alpha) / g$.

• Sprawy się komplikują dla wysokości początkowych różniących się od 0. Wtedy musimy podstawić długi wzór z poprzedniego kroku jako $t$:

• Zasięg jest szczególnie ważny w balistyce. Omówiliśmy ten przypadek szczegółowo w kalkulatorze współczynnika balistycznego 🇺🇸.

5. Oblicz maksymalną wysokość.

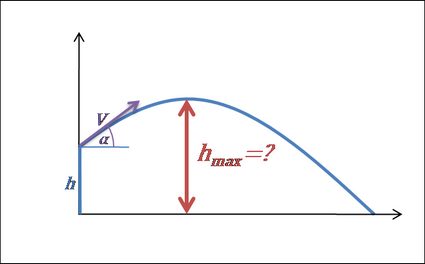
• Gdy pocisk osiąga maksymalną wysokość, przestaje poruszać się w górę i zaczyna spadać. Oznacza to, że jego składowa prędkości pionowej zmienia się z dodatniej na ujemną — innymi słowy, jest równa 0 przez krótką chwilę w czasie $t(V_\mathrm y=0)$.
• Jeśli $V_\mathrm{y0} - g t(V_\mathrm y=0) = 0$, to możemy przepisać to równanie na $t(V_\mathrm y=0) = V_\mathrm{y0} / g$.
• Teraz po prostu znajdujemy odległość od ziemi w tym czasie:

• Na szczęście w przypadku rzutu ukośnego z jakiejś początkowej wysokości $h$ musimy po prostu dodać tę wartość do końcowego wzoru:

Uff, to było mnóstwo obliczeń! Podsumujmy to tak, aby zestawić najistotniejsze równania ruchu pocisków:

1. Wyrzucenie obiektu z ziemi (wysokość początkowa h = 0):

• Składowa pozioma prędkości: $V_\mathrm x = V_0 \cos \alpha$
• Składowa pionowa prędkości: $V_\mathrm y = V_0 \sin \alpha - gt$
• Czas lotu: $t = 2 V_\mathrm{y0} / g$
• Zasięg rzutu: $R = 2 V_\mathrm x V_\mathrm{y0} / g$
• Wysokość maksymalna: $h_\mathrm{max} = V^2_\mathrm{y0} / (2 g)$

2. Wyrzucenie obiektu z jakiegoś poziomu (wysokość początkowa h > 0):

• Składowa pozioma prędkości: $V_\mathrm x = V_0 \cos \alpha$
• Składowa pionowa prędkości: $V_\mathrm y = V _0 \sin \alpha - gt$
• Czas lotu: $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Zasięg rzutu: $R = V_\mathrm x \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Maksymalna wysokość: $h_\mathrm{max} = h + V^2_ \mathrm{y0} / (2 g)$

Korzystanie z naszego kalkulatora rzutu ukośnego z pewnością pozwoli ci zaoszczędzić sporo czasu. Może on również działać „w inną stronę”. Na przykład wpisz czas lotu, odległość poziomą i wysokość początkową, a później zobacz jak wykonuje wszystkie obliczenia za ciebie!

Koniecznie sprawdź też kalkulator paraboli, aby dowiedzieć się więcej o tej krzywej z matematycznego punktu widzenia.