Kalkulator płaskiej a okrągłej Ziemi

Jaki jest najlepszy sposób na poznanie świata? Proponujesz teorię i starasz się ją udowodnić za pomocą obserwacji (nauka)? A może po prostu wymyślasz rzeczy i ignorujesz oczywiste fakty (nonsens)? W Omni uważamy, że pierwsza opcja sprawdza się całkiem nieźle. Dzięki niej dotarliśmy na Księżyc, prawda? Nawiasem mówiąc, naprawdę tak było.

Aby uczcić Światowy Dzień Nauki dla Pokoju i Rozwoju, obchodzony co roku 10 listopada, stworzyliśmy kalkulator, który pomoże ci walczyć z bzdurami, półprawdami i ściemami. Nasze narzędzie działa także na rzecz nauki i otwartości umysłu.

Omni kalkulator płaskiej a okrągłej Ziemi zawiera eksperymenty, które pomogą ci udowodnić, że Ziemia jest rzeczywiście okrągła. Nie martw się, nie będziesz budować własnej rakiety, która poleci w kosmos, aby to sprawdzić (lub obliczyć jej impuls i pęd 🇺🇸 oraz jej energię kinetyczną).

Mamy dla ciebie trzy stosunkowo proste eksperymenty do wypróbowania:

• Zachód słońca widziany dwa razy — Zmieniając punkt widzenia nad powierzchnią Ziemi, możesz zobaczyć zachód Słońca dwa razy. Nasz kalkulator powie ci, ile z drugiego zachodu słońca zobaczysz.
• Znikające obiekty na horyzoncie — Ukryj obiekty za krzywizną Ziemi, zmieniając wysokość punktu widzenia. Nasz kalkulator pokaże ci, jak wysoki może być zanikający obiekt.
• Cienie rzucane przez wbite w ziemię patyki — Użyj długości cieni rzucanych przez patyki wbite w różnych miejscach, aby oszacować obwód Ziemi.

Zanim przejdziemy do eksperymentów, krótko omówmy, dlaczego ludzie mogą wierzyć, że Ziemia jest płaska i jaki model świata przedstawiają.

Zadziwiające jest to, że nawet w najbogatszym, najbardziej rozwiniętym technologicznie kraju na świecie, jakim są Stany Zjednoczone, jeden na sześciu mieszkańców nie jest pewien, czy Ziemia jest okrągła 🤔. Jak wynika z badania IBSP (Ogólnopolska Grupa Badawcza), Polacy nie tak chętnie wierzą płaskoziemcom, ale aż 4 proc. respondentów uważa, że Ziemia jest płaska.
Istnieją przypuszczenia, że wiara w płaską Ziemię może wynikać z wysoce indywidualistycznej kultury oraz braku zaufania do autorytetów, instytucji i ekspertów.

Płaskoziemcy wydają się patrzeć na świat samodzielnie, bez odniesienia do ponad 2000 lat ludzkich odkryć. Wow, sporo ich ominęło. Są również bardzo nieufni wobec wszelkich faktów, których sami nie zweryfikowali. Porozmawiajmy o problemach z zaufaniem.

Następnie podejmują się niezwykłych wyzwań, aby udowodnić, że Ziemia jest płaska, podczas gdy istnieją proste rzeczy, które mogliby zrobić, aby udowodnić, że Ziemia jest okrągła. Oto kilka przykładów:

• „Szalony” Mike Hughes zbudował własną rakietę napędzaną parą, aby polecieć na wysokość 572 metrów i sfotografować brak krzywizny pustyni Mojave oraz udowodnić, że Ziemia ma kształt dysku. Niestety, aby zobaczyć krzywiznę Ziemi, musiałby wznieść się na wysokość co najmniej 11 000 metrów. Szalony Mike zginął w lutym 2020 roku podczas próby lotu własnoręcznie zbudowaną rakietą.
• Gwiazda YouTube Logan Paul dotarł na Antarktydę, aby znaleźć krawędź płaskiej Ziemi. Mamy nadzieję, że spakował dużo zapasów na dłuższą podróż, ponieważ trasa z jednego krańca Antarktydy na drugi liczy około 5000 km.
• Raper B.o.B próbował crowdfundingowo wystrzelić własnego satelitę, aby sprawdzić, czy Ziemia jest płaska. Ostatecznie udało mu się zebrać tylko 6 883 z zakładanego 1 miliona dolarów, nawet pomimo medialnego szumu i „wsparcia” ze strony emerytowanych astronautów. No cóż, nieważne. Może zamiast tego B.o.B. mógłby wypróbować jeden z naszych prostych, tanich eksperymentów.

Ta kreskówka autorstwa Toma Fondera dość dobrze podsumowuje płaskoziemców.

W modelu płaskiej Ziemi świat jest dyskiem (podobnym do kół zębatych używanych do redukcji biegów) z centralnie położonym biegunem północnym. Wokół krawędzi dysku znajduje się ściana lodu i śniegu pochodzącego z „bieguna południowego”. Tworzy to lodową barierę, przypuszczalnie w celu powstrzymania wody z oceanów przed wypadnięciem z dysku w przestrzeń kosmiczną.

Grubość płaskiego dysku Ziemi nie jest znana. Jednak masa musi być znacznie mniejsza niż w przypadku okrągłej Ziemi, więc płaska Ziemia nie byłaby w stanie utrzymać swojej atmosfery. W tej wizji nad Ziemią być może znajduje się przezroczysta kopuła, która powstrzymuje ją przed ucieczką.

Tradycyjny model płaskiej Ziemi zakłada, że Słońce znajduje się nad dyskiem, krążąc po niebie jak dziecięcy telefon komórkowy i w znacznie mniejszej odległości. To nie wyjaśnia zachodów i wschodów słońca. Aby zachować zdrowy rozsądek, wyobraźmy sobie, że dysk obraca się jak moneta względem Słońca. To przynajmniej przywróciłoby wschód i zachód słońca (coś, co mogłoby zaobserwować najprostsze zwierzę). Nie byłoby jednak stref czasowych, ponieważ wschód i zachód słońca miałyby miejsce w tym samym czasie na całym świecie.

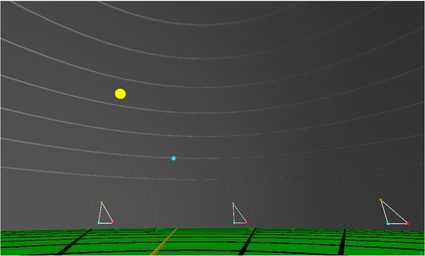
To jest główny problem z modelem płaskiej Ziemi. Jest on pełen niespójności i niewyjaśnionych obserwacji. Na przykład, dlaczego jest zimno zarówno w centrum, jak i na obrzeżach dysku?

Wróćmy do bardziej naukowego sposobu myślenia i przeprowadźmy pierwszy eksperyment.

Ten pierwszy eksperyment może być naprawdę prosty do wykonania. Poruszaj się w górę wystarczająco szybko, aby wyprzedzić cień rzucany przez horyzont. Będziesz wtedy w stanie zobaczyć część zachodu słońca dwa razy! Jeśli to zaobserwujesz, Ziemia rzeczywiście jest okrągła. Ten eksperyment obliczy, ile z drugiego zachodu słońca możesz zobaczyć i jak długo może trwać zachód słońca.

Co byś zobaczył/a, gdyby Ziemia była płaska? Nie byłoby żadnego drugiego zachodu słońca 😭. Bez względu na to, jak wysoko lub szybko trwałaby podróż z powierzchni płaskiej Ziemi; nie zobaczysz słońca aż do świtu.

W przypadku okrągłej Ziemi, gdy słońce zachodzi, wyobraź sobie cień rzucany przez horyzont Ziemi zbliżający się do ciebie i przesuwający się w górę twojego ciała. Jeśli możesz wyprzedzić ten cień, poruszając się w górę wystarczająco szybko, możesz ponownie zobaczyć zachód słońca. Teraz przyjrzyjmy się matematyce.

Ten artykuł daje nam równanie, które wiąże czas z wysokością cienia:

t = 8 ⋅ √h,

gdzie t to czas, w którym cień przesuwa się na wysokość o wartości h. Możemy odnieść h do różnicy wysokości między dwiema wysokościami, a t do czasu potrzebnego na przemieszczenie się w górę. Ponieważ nie możemy natychmiast przemieścić się z niższej wysokości na wyższą, musimy wziąć pod uwagę czas podróży. Wreszcie, aby znaleźć ułamek drugiego zachodu słońca, który możemy ponownie zobaczyć, musimy znać całkowity czas trwania zachodu słońca. Następnie mamy to równanie dla procentu zachodu słońca, który zaobserwujesz ponownie:

Procent drugiego zachodu słońca = 100 ⋅ (1 - ((czas trwania zachodu słońca - t - czas podróży) / całkowity czas trwania zachodu słońca))

Istnieje kilka sposobów, aby ponownie zobaczyć słońce tuż po zachodzie, w różnym stopniu. Omni kalkulator płaskiej a okrągłej Ziemi powie ci, ile z drugiego zachodu słońca będziesz w stanie zaobserwować. Przyjrzyjmy się trzem pomysłom, na które wpadliśmy.

1. Połóż się, wstań

Ten pomysł jest najprostszy pod względem wykonania i dostępności sprzętu. Potrzebujesz tylko miejsca, w którym możesz zobaczyć słońce zachodzące na tle morza lub bardzo płaskiego terenu (np. równiny). Piękne, bezchmurne niebo również będzie pomocne. Wszystko, co musisz zrobić, to obserwować zachód słońca leżąc. Gdy przestaniesz widzieć słońce, natychmiast wstań tak szybko, jak to możliwe. Powinieneś/aś być w stanie ponownie zobaczyć niewielką część górnej części słońca.

Tutaj dowiesz się, jak za pomocą naszego kalkulatora obliczyć, ile dokładnie zobaczysz z drugiego zachodu słońca.

1. Wybierz najbliższą lokalizację lub ręcznie wprowadź czas trwania zachodu słońca w miejscu, w którym się znajdujesz.
2. Wprowadź dolną wysokość początkową swojego poziomu oczu. W tym przypadku w pozycji leżącej. Zalecamy wysokość około 20 cm.
3. Wprowadź, ile czasu zajmie ci osiągnięcie wyższej wysokości. Naszym zdaniem około pół sekundy, ale zmierz sobie czas, aby się upewnić.
4. Wprowadź ostateczną wysokość poziomu oczu, gdy stoisz. Możesz to zmierzyć, odejmując od swojego wzrostu odległość od czubka głowy do poziomu oczu.
5. Następnie zobaczysz procent Słońca, który będziesz w stanie ponownie zobaczyć. Chcesz widzieć więcej? Spróbuj zmienić wartości w kalkulatorze lub przejdź do bardziej zaawansowanych wariantów eksperymentu poniżej.

Dzięki tej metodzie powinieneś/aś być w stanie zobaczyć około 5% drugiego zachodu słońca.

2. Szybka winda w górę wieżowca

Aby zobaczyć więcej drugiego zachodu słońca, musisz wznieść się wyżej i szybciej, aby wyprzedzić cień horyzontu. Jedną z opcji jest wieżowiec z szybką windą. Zjawisko to zostało zaobserwowane w hotelu Burj Khalifa w Dubaju.

Aby wybrać wartości wejściowe dla tego wieżowca, wybierz „Winda wieżowca — Burj Khalifa” (ang. „Skyscraper lift — Burj Khalifa hotel”) z listy pomysłów. Jeśli chcesz wypróbować tę funkcję w innym budynku, dostosuj odpowiednio wartości wejściowe.

Powinieneś/aś być w stanie ponownie zobaczyć 88% zachodu słońca, a tym samym prawie podwoić czas jego trwania. Jeśli jesteś miłośnikiem zachodów słońca, jest to najlepsza rzecz do zrobienia.

3. Dron z kamerą

Innym pomysłem jest użycie dobrej jakości drona, który ma możliwość transmitowania obrazu na żywo. Znaleźliśmy drona, który może osiągnąć wysokość 1000 metrów w 200 sekund. Jeśli wybierzesz z listy pomysłów opcję „Dron”, zobaczysz, że dzięki tej metodzie powinieneś/aś zobaczyć około jedną trzecią zachodu słońca.

Sprawdź, jak szybko i wysoko może latać twój dron i odpowiednio dostosuj wartości w naszym kalkulatorze.

W tym eksperymencie ukryjemy część obiektu za krzywizną Ziemi. Musisz znaleźć zbiornik wodny, którego odległy brzeg znajduje się w odległości co najmniej 2 km, a dzień musi być spokojny i bezwietrzny.

Ponadto, aby uniknąć efektu mirażu (fatamorgany, załamania światła), przeprowadź eksperyment rano, gdy jest chłodno. Dlatego też nie zalecamy korzystania z pustyni — efekt mirażu sprawi, że nie będziesz w stanie dostrzec obiektów na odległym brzegu wystarczająco wyraźnie.

Autor poniższego filmu sprawił, że ciężarówka oddalona o 7 km zniknęła po drugiej stronie jeziora, obniżając kamerę bliżej ziemi.

Ewentualnie farma wiatrowa na morzu również jest dobrą opcją, co pokazuje to zdjęcie:

Zauważ, że im dalej znajduje się wiatrak, tym bardziej jest ukryty. O to właśnie chodzi w tym eksperymencie — o obliczenie, jaką część odległego obiektu możesz ukryć za krzywizną Ziemi.

W tym eksperymencie zaczniemy od wysokiego punktu widzenia, a następnie zejdziemy do niskiego punktu widzenia, aby zasłonić odległy obiekt. Z matematycznego punktu widzenia sprawdzimy, jaka część obiektu jest ukryta przy wysokim i niskim punkcie widzenia, a następnie obliczymy różnicę.

Aby obliczyć wysokość przesłaniania, musimy najpierw znać odległość do horyzontu. Określa ją poniższe równanie:

a = √[(r + h)² - r²]

gdzie:

• a to odległość od twojego położenia do horyzontu,
• h to wysokość punktu widzenia nad ziemią, oraz
• r to promień Ziemi, równy 6371 km.

Następnie wprowadzamy wynik do drugiego równania, które oblicza, jaka część obiektu jest zasłonięta, x, jeśli patrzysz z zerowej wysokości:

x = √(a² - 2ad + d² + r²) - r

Różnica pomiędzy dwiema wartościami x jest wysokością obiektu, którego zanik możemy zauważyć, zmieniając wysokość naszego punktu widzenia.

OK, więc znalazłeś/aś doskonałą lokalizację, taką jak jezioro z brzegiem oddalonym o kilka kilometrów. Aby zobaczyć jakiekolwiek obiekty na odległym brzegu, będziesz potrzebować dobrej lornetki. Jeszcze lepszym rozwiązaniem będzie kamera wideo z silnym obiektywem zmiennoogniskowym. Pozwoli ci to również na nagranie eksperymentu tak jak na powyższym filmie.

Aby uzyskać stabilny widok przez lornetkę lub kamerę, zalecamy zamontowanie ich na statywie. Użycie statywu pozwoli ci również na dokładny pomiar dwóch wysokości.

Tutaj dowiesz się, jak użyć naszego kalkulatora, aby dowiedzieć się, jak duży obiekt może zniknąć za krzywizną Ziemi.

1. Zmierz odległość do odległego brzegu jeziora. Możesz użyć do tego papierowej mapy lub funkcji pomiaru trasy w Google Maps. Wprowadź odległość do zmiennej „Odległość do obiektu” w kalkulatorze.
2. Zmierz wysokość nad ziemią na poziomie oczu w pozycji stojącej lub wysokość kamery w pozycji wysokiej. Wprowadź tę wysokość w następnym polu.
3. Zrób to samo, gdy leżysz lub kamera znajduje się w pozycji niskiej. Aby zmaksymalizować efekt, spróbuj znaleźć się jak najniżej poziomu wody.
4. Zobaczysz wtedy, że zostanie obliczona wysokość obiektu, który jest zasłonięty przez krzywiznę Ziemi. Jeśli obiekt wydaje się zbyt mały, spróbuj zwiększyć wysokość w pozycji stojącej i zmniejszyć wysokość w pozycji niskiej.

Jeśli Ziemia jest płaska, nie zobaczysz żadnej różnicy w obiektach po drugiej stronie jeziora, niezależnie od tego, jak nisko nad ziemią je widzisz.

Ten eksperyment nie tylko udowadnia, że Ziemia jest okrągła, ale także pozwala oszacować jej obwód. Dokładnie to samo zrobił grecki matematyk Eratostenes w Aleksandrii około 240 roku p.n.e. Wiedział on, że w Asuanie, około 800 km na południe, znajduje się studnia, do której światło słoneczne dociera w południe podczas przesilenia letniego. W tym samym czasie zmierzył cień rzucany przez kij w Aleksandrii.

Zakładając, że Ziemia jest okrągła, a Słońce jest daleko, i używając matematyki, którą omówimy poniżej, Eratostenes doszedł do wniosku, że obwód Ziemi był około 50 razy większy niż odległość między Aleksandrią a Asuanem. To wynik różny o około 10% od poprawnej odpowiedzi. Fantastyczny wynik jak na tak prosty eksperyment przeprowadzony ponad 2000 lat temu.

Patrząc na trójkąt utworzony przez patyk i cień, możemy użyć funkcji arcus tangens (odwrotnej do tangensa), aby obliczyć kąt między kijem a promieniem słonecznym, korzystając z równania:

θ = arctg(długość cienia / wysokość kija)

Tak więc robimy to dla dwóch lokalizacji. Jak te dwa kąty odnoszą się do obwodu Ziemi? Poniższy rysunek pomoże nam odpowiedzieć na to pytanie.

Posługując się zasadami geometrii, możemy pokazać, że kąt α między liniami przechodzącymi przez lokalizacje A i B a środkiem Ziemi jest różnicą kątów cienia patyka:

α = θ₂ - θ₁

Znamy teraz długość łuku (odległość wzdłuż powierzchni Ziemi) między A i B oraz kąt α. To pozwala nam po prostu przeskalować odległość do pełnego obwodu Ziemi, używając równania:

Obwód Ziemi = Odległość A → B ⋅ (360° / α)

Ważne jest, aby pamiętać, że odległość od A do B powinna być odległością, którą możesz podróżować tylko w kierunku północnym lub południowym (odległość północ-południe). Potrzebujemy takiej odległości, ponieważ tylko wtedy, gdy podróżujesz na północ, cień rzucany przez kij staje się dłuższy.

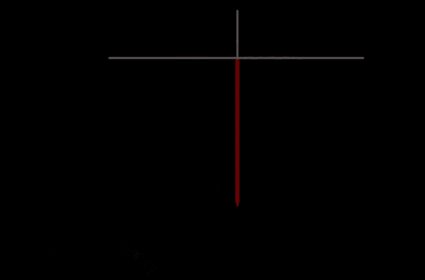
Zakładając, że punkt A znajduje się na południe od punktu B, narysuj na mapie linię biegnącą na północ od punktu A. Następnie narysuj linię biegnącą na wschód od punktu B. Odległość północ-południe to długość od punktu A do miejsca, w którym obie narysowane linie przecinają się.

Istnieją dwa podstawowe sposoby przeprowadzenia tego eksperymentu. Możesz samemu podróżować na znaczną odległość w kierunku północy lub południa (większą niż 160 kilometrów, ale im dalej, tym lepiej) lub współpracować z kimś, kto mieszka na tyle daleko, aby ci pomóc.

Zacznijmy od opcji podróży. Najlepiej jest próbować tego w okolicach najkrótszego lub najdłuższego dnia w roku, ponieważ wówczas długość dnia jest stosunkowo stabilna. Zmniejszy to błędy w pomiarze kąta rzucanego przez cień w dwóch lokalizacjach. Poniżej znajdziesz instrukcje krok po kroku:

1. Zmierz długość swojego patyka. Musisz ją wpisać w pierwszym polu kalkulatora. Jeśli część patyka znajduje się w ziemi, uwzględnij tylko długość nad ziemią.
2. Zmierz długość cienia w lokalizacji A w południe czasu lokalnego. Jeśli nie ma słonecznego dnia, poczekaj, aż taki się pojawi. Wprowadź długość rzucanego cienia do kalkulatora, a zostanie obliczony kąt, pod jakim pada cień.
3. Udaj się do lokalizacji B i wykonaj te same czynności, co w kroku 2.
4. Korzystając z mapy, zmierz odległość północ-południe między dwoma lokalizacjami i wprowadź tę liczbę do kalkulatora (patrz na instrukcje powyżej).
5. Następnie otrzymasz odpowiedź na temat zmierzonego szacunkowego obwodu Ziemi i tego, jak blisko byłeś/aś prawdziwej odpowiedzi.

Jeśli masz znajomego w innej lokalizacji, który może ci pomóc, kroki są zasadniczo takie same. Upewnij się, że oba patyki są tej samej długości i że mierzysz cień w południe czasu lokalnego tego samego dnia. Ta opcja jest znacznie łatwiejsza i można ją wykonać w każdy słoneczny dzień w roku.

Powiedzmy, że podróżujemy na północ z Krakowa do Gdańska (A do B), pokonując odległość północ-południe wynoszącą około 600 km. Kij ma długość 90 cm (0,9 m) i mierzymy długość cienia 0,9 metra w punkcie A. Oznacza to kąt cienia 45°. Następnie udajemy się do punktu B i mierzymy cień o długości 1,08 metra, co oznacza, że kąt cienia wynosi tutaj około 50,2°.

Po wprowadzeniu wszystkich danych do kalkulatora otrzymamy wynik 41 583 km. A zatem różnica między obliczonym i rzeczywistym obwodem Ziemi mierzonym od bieguna do bieguna (równym 40 008 km) wynosi mniej niż 4%.

Wyobraźmy sobie przez chwilę, że płaskoziemcy mają rację. Jak powyższy przykład działa w modelu płaskiej Ziemi?

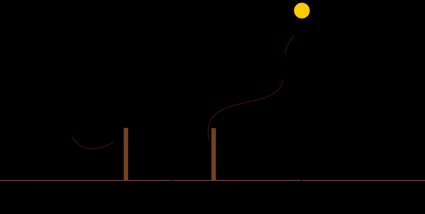
W modelu płaskiej Ziemi patyki nadal będą rzucać cień o różnej długości. Jednak wykonanie obliczeń trygonometrycznych prowadzi do dziwnego wyniku. Odnosząc się do powyższego diagramu i stosując wspomnianą trygonometrię, możemy powiedzieć, że:

d = h ⋅ |tg θ₂ - tg θ₁|

Używając kątów 45° i 50,2° oraz 600 km dla d, widzimy, że odległość do słońca h wynosi

h = 600 / (1,19 - 1) = 3158 km

To zupełnie inna odległość. Dodatkowo model płaskiej Ziemi może wskazywać, że Słońce jest znacznie mniejsze, niż stwierdziła nauka.

Teraz możemy obliczyć dwie inne odległości do Słońca z dwóch lokalizacji:

R₁ = h / cos θ₁ = 3158 / cos(45°) = 4466 km

R₂ = h / cos θ₂ = 3158 / cos(50,2°) = 4913 km

Wynik ten oznacza, że po przebyciu 600 km na południe Słońce powinno zmniejszyć się o około 10%. W rzeczywistości, jak możesz sam sprawdzić, Słońce nie wydaje się zmniejszać, gdy podróżujesz na południe.

Dlatego możemy stwierdzić, że model płaskiej Ziemi jest błędny. Nie zgadza się on z obserwacjami, co stanowi kluczową cechę każdego poważnego modelu naukowego. Musi on zgadzać się z wynikami eksperymentów.

Koncepcja, że Ziemia ma kształt kuli, jest dość stara! W starożytnej Grecji naukowcy i filozofowie byli świadomi tego faktu już w V wieku p.n.e.

Nawet w późniejszych wiekach model kulisty był bardziej powszechnie akceptowany i tylko w marginalnym stopniu kwestionowany poza czysto mitologicznymi podstawami: pozorne odrodzenie się tej teorii i jej znaczenie w czasach współczesnych jest wyłącznie konsekwencją zmiany naszych metod komunikacji.

Oblicz obwód Ziemi za pomocą cieni:

1. Poproś znajomego mieszkającego na innej szerokości geograficznej o wykonanie tych samych czynności co ty, a następnie:
2. Pionowo umieść patyk o znanej długości w ziemi.
3. Zmierz kąt pomiędzy kijem a promieniami słonecznymi o danej porze dnia.
4. Użyj wzoru:
   θ = arctg(długość cienia / wysokość kija).
5. Teraz użyj tego wzoru dla obwodu Ziemi:
   Obwód Ziemi = Odległość ⋅ (360° / α),
   gdzie:
   • Odległość to odległość północ-południe między patyczkami
   • α to różnica między kątami obliczonymi wcześniej.

Aby zobaczyć krzywiznę Ziemi, musisz znajdować się na wysokości około 10,5 km. Jest to mniej więcej wysokość przelotowa samolotu pasażerskiego. Jednak, aby zobaczyć prawidłowo krzywiznę globu, potrzebujesz całkowicie czystego horyzontu (bez chmur) i pola widzenia co najmniej 60 stopni. Oba te warunki rzadko są spełnione z okien samolotu, ale możesz spróbować.

Zauważ też, że krzywizna nie jest widoczna nawet ze szczytu Mount Everest!

Aby udowodnić, że Ziemia jest okrągła, idź na plażę! Jeśli masz przed sobą wystarczająco długi odcinek morza, możesz po prostu poczekać, aż statek zbliży się do wybrzeża. Najpierw zobaczysz jego górną część pojawiającą się nad horyzontem, a następnie powoli resztę statku.
Ponieważ Ziemia jest okrągła, jej krzywizna zakrywa część statku. Zakryta część zmniejsza się, gdy statek zbliża się do ciebie.

Teraz najtrudniejszą częścią jest przekonanie sceptyków, że taka jest ostateczna odpowiedź!