Eigenschappen van een zeshoek berekenen

Welkom bij de hexagon calculator, een handig hulpmiddel bij het berekenen van regelmatige zeshoeken. De zeshoek is een van de populairste vormen in de natuur, van honingraatpatronen tot zeshoekige tegels voor spiegels - de toepassingen zijn bijna eindeloos. Hier leggen we niet alleen uit waarom de zeshoek zo populair is, maar ook hoe je de zijden van een zeshoek correct tekent. We beantwoorden ook de vraag "wat is een zeshoek?" met behulp van de definitie van een zeshoek.

Met onze zeshoek calculator kun je veel meetkundige eigenschappen en berekeningen ontdekken, zoals hoe je de oppervlakte van een zeshoek kunt berekenen. Je leert ook hoe je de calculator kunt gebruiken om elke analyse met betrekking tot deze zeshoekige vorm te vereenvoudigen.

Het zal geen verrassing zijn dat de zeshoek (ook wel "Hexagoon" genoemd) precies zes zijden heeft. Dit geldt voor alle zeshoeken, omdat het hun bepalende kenmerk is. De lengte van de zijden kan zelfs binnen dezelfde zeshoek variëren, behalve bij de regelmatige zeshoek, waarbij alle zijden even lang moeten zijn.

We zullen later wat dieper op zo'n vorm ingaan als we behandelen hoe we de oppervlakte van een zeshoek kunnen vinden. Voor nu volstaat het om te zeggen dat de regelmatige zeshoek de meest voorkomende zeshoek is en het meest voorkomt in de natuur.

Er zal een hele paragraaf worden gewijd aan de belangrijke eigenschappen van de regelmatige zeshoek, maar eerst moeten we het technische antwoord weten op: "Wat is een zeshoek?" Het beantwoorden van deze vraag helpt ons de trucs te begrijpen die we kunnen gebruiken om de oppervlakte van een zeshoek te berekenen zonder de formule voor de oppervlakte van een zeshoek blindelings te gebruiken. Deze trucs maken gebruik van andere veelhoeken, zoals vierkanten, driehoeken en zelfs parallellogrammen.

Zoals we al hebben gezegd, moeten alle zijden van de regelmatige zeshoek even lang zijn en moeten alle binnenhoeken in de zeshoek gelijk zijn. Elke zijde is even lang (zolang dit geldt voor alle 6 zijden!), dus het berekenen van de omtrek van een zeshoek is zo eenvoudig dat je niet eens de omtrek van een veelhoek calculator 🇺🇸 nodig hebt. Je kunt gewoon de volgende berekening gebruiken:

• omtrek = 6 × zijde

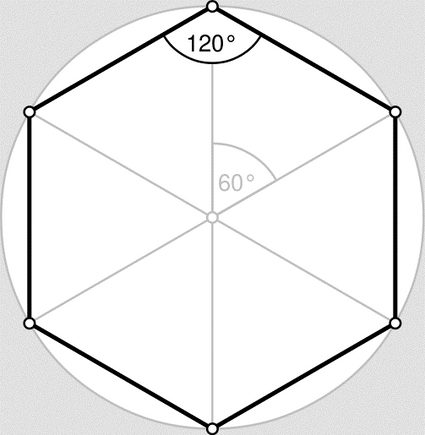
De hoeken van een willekeurige zeshoek kunnen elke waarde hebben, maar ze moeten allemaal samen 720º zijn (je kunt ze eenvoudig omrekenen naar andere eenheden met onze hoekconversie calculator 🇺🇸). Omdat de regelmatige zeshoek vereist dat alle hoeken gelijk zijn, volgt hieruit dat elke individuele hoek 120º moet zijn. Dit gegeven blijkt heel belangrijk te zijn als we het hebben over de populariteit van de zeshoek in de natuur. Het zal ook van pas komen als we uitleggen hoe we de oppervlakte van een regelmatige zeshoek kunnen vinden. We zullen het ook gebruiken om de oppervlakteformule voor regelmatige zeshoeken te vinden.

We zullen nu bekijken hoe je de oppervlakte van een zeshoek kunt vinden met behulp van verschillende trucs. De eenvoudigste manier is om onze zeshoek calculator te gebruiken, die een ingebouwde oppervlakte conversie tool bevat. Voor degenen die willen weten hoe ze dit met de hand moeten doen, leggen we uit hoe je de oppervlakte van een regelmatige zeshoek kunt vinden met en zonder de formule voor de oppervlakte van een zeshoek. De formule voor de oppervlakte van een veelhoek is altijd hetzelfde, ongeacht het aantal zijden, zolang het een regelmatige veelhoek is:

• oppervlakte = apothema × omtrek / 2

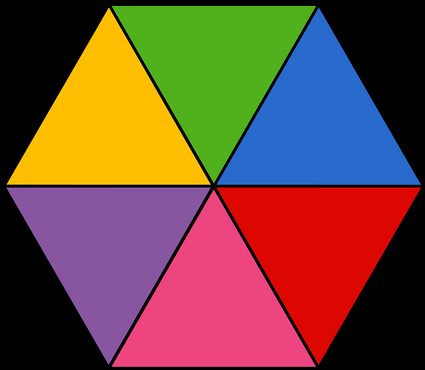
Ter herinnering, de apothema is de afstand tussen het midden van een zijde en het middelpunt. Je kunt het zien als de hoogte van de gelijkzijdige driehoek die wordt gevormd door één zijde en twee stralen van de zeshoek te nemen (elk van de gekleurde gebieden in de afbeelding hierboven). Je kunt de apothema ook zien als de afstand tussen het middelpunt en een willekeurige zijde van de zeshoek, omdat de Euclidische afstand wordt gedefinieerd met behulp van een loodrechte lijn.

Als je de formule niet meer weet, kun je altijd denken aan de zeshoek als een verzameling van 6 driehoeken. Voor de regelmatige zeshoek zijn deze driehoeken gelijkzijdige driehoeken. Dit feit maakt het veel eenvoudiger om de oppervlakte te berekenen dan wanneer het gelijkbenige driehoeken zouden zijn of zelfs 45 45 90 driehoeken zoals in het geval van een vierkant.

Voor de regelmatige driehoek hebben alle zijden dezelfde lengte, namelijk de lengte van de zijde van de zeshoek die ze vormen. We noemen dit a. En de hoogte van een driehoek is h = √3/2 × a, wat in dit geval de exacte waarde van de apothema is. We herinneren je eraan dat √ de vierkantswortel betekent. Hiermee kunnen we beginnen met de berekening:

• A₀ = a × h / 2
• = a × √3/2 × a / 2
• = √3/4 × a²

Waarbij A₀ de oppervlakte is van elk van de gelijkzijdige driehoeken waarin we de zeshoek hebben verdeeld. Nadat we deze oppervlakte met zes vermenigvuldigen (omdat we 6 driehoeken hebben), krijgen we de formule voor de oppervlakte van de zeshoek:

• A = 6 × A₀ = 6 × √3/4 × a²

• A = 3 × √3/2 × a²

• = (√3/2 × a) × (6 × a) /2

• = apothema × omtrek /2

We hopen dat je kunt zien hoe we tot dezelfde formule voor de oppervlakte van een zeshoek komen die we eerder hebben genoemd.

Als je het was meer opwindend wilt maken, kun je spelen met andere vormen. Stel bijvoorbeeld dat je de zeshoek in tweeën deelt (van hoekpunt tot hoekpunt). In dat geval krijg je twee trapeziums en kun je de oppervlakte van de zeshoek berekenen als de som daarvan. Je kunt ook twee aangrenzende driehoeken combineren om in totaal 3 verschillende ruiten te construeren en de oppervlakte van elk afzonderlijk berekenen. Je kunt de zeshoek zelfs ontbinden in een grote rechthoek (met behulp van de korte diagonalen) en 2 gelijkbenige driehoeken!

Probeer dit gerust met verschillende vormen en calculators om te zien welke andere trucs je kunt bedenken. Probeer alleen rechthoekige driehoeken of misschien zelfs speciale rechthoekige driehoeken te gebruiken om de oppervlakte van een zeshoek te berekenen!

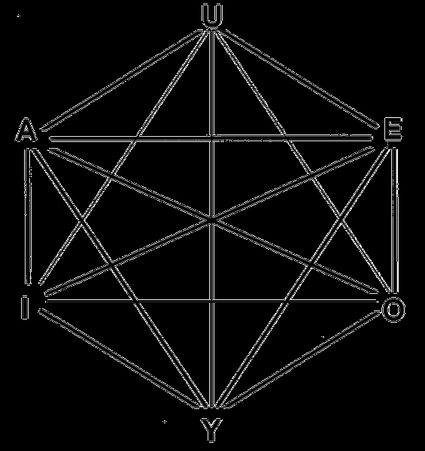
Het totale aantal diagonalen van de zeshoek is gelijk aan 9 - drie daarvan zijn lange diagonalen die het centrale punt kruisen, en de andere zes zijn de zogenaamde "hoogte" van de zeshoek.
Onze zeshoek calculator kan je ook wat vervelende berekeningen besparen over de lengtes van de diagonalen van de zeshoek. Hier zie je hoe je de twee soorten diagonalen berekent:

• Lange diagonalen - Ze kruisen altijd het centrale punt van de zeshoek. Zoals je in de afbeelding hierboven kunt zien, is de lengte van zo'n diagonaal gelijk aan twee randlengtes:

  D = 2 × a

• Korte diagonalen - Ze kruisen het centrale punt niet. Ze worden geconstrueerd door twee hoekpunten met elkaar te verbinden en er precies één tussen te laten. Hun lengte is gelijk aan d = √3 × a.

Een ander paar waarden die belangrijk zijn in een zeshoek zijn de omtrekstraal en de binnenstraal. De omtrekstraal is de straal van de omtrek die alle hoekpunten van de regelmatige zeshoek bevat. De binnenstraal is de straal van de grootste cirkel die volledig binnen de zeshoek ligt.

• Omtrekstraal: om de straal te vinden van een cirkel omgeschreven op de regelmatige zeshoek, moet je de afstand bepalen tussen het centrale punt van de zeshoek (dat ook het middelpunt van de cirkel is) en een van de hoekpunten. Dit is eenvoudigweg gelijk aan R = a.

• Binnenstraal: de straal van een cirkel ingeschreven in de regelmatige zeshoek is gelijk aan de helft van de hoogte, die ook de apothema is: r = √3/2 × a.

Nu gaan we een meer praktische en minder wiskundige wereld verkennen: hoe teken je een zeshoek. Voor een willekeurige (onregelmatige) zeshoek is het antwoord eenvoudig: teken een willekeurige 6-zijdige vorm zodat het een gesloten veelhoek is, en je bent klaar. Maar voor een regelmatige zeshoek is het niet zo eenvoudig omdat we ervoor moeten zorgen dat alle zijden even lang zijn.

Voor het perfecte resultaat heb je een tekenkompas nodig. Teken een cirkel en begin er, met dezelfde straal, markeringen langs te maken. Begin bij een willekeurig punt en maak de volgende markering met het vorige als ankerpunt, trek een cirkel met de passer. Je eindigt met 6 markeringen en als je ze met rechte lijnen verbindt, heb je een regelmatige zeshoek. Je kunt een soortgelijk proces zien in de animatie hierboven.

Met de zeshoek calculator kun je verschillende interessante parameters berekenen van de zeshoekige vorm die we gewoonlijk een zeshoek noemen. Het gebruik van deze calculator is zo eenvoudig als het maar kan. Je hebt slechts één van de parameters nodig om alle andere te berekenen, en bevat een ingebouwd hulpmiddel voor het omrekenen van lengtes voor elk van de parameters.

We hebben alle parameters van de calculator besproken, maar voor de duidelijkheid en volledigheid zullen we ze nu kort bespreken:

• Oppervlakte - 2-D oppervlak omsloten door de zeshoekige vorm;
• Zijlengte - Afstand van een hoekpunt tot het volgende opeenvolgende hoekpunt;
• Omtrek - Som van de lengtes van alle zijden van een zeshoek;
• Lange diagonaal - afstand van een hoekpunt tot het tegenoverliggende hoekpunt;
• Korte diagonaal - afstand tussen twee hoekpunten waartussen een ander hoekpunt ligt;
• Omtrekstraal - afstand van het middelpunt tot een hoekpunt (hetzelfde als de straal van de zeshoek); en
• Binnenstraal - hetzelfde als de apothema.

Iedereen houdt van een goede toepassing in de praktijk, en zeshoeken zijn beslist een van de meest gebruikte veelhoeken ter wereld. Om met het gebruik door mensen te beginnen, het eenvoudigste (en waarschijnlijk minst opwindende) gebruik zijn Zeshoekige tegels voor vloeren. De zeshoek is een uitstekende vorm omdat deze perfect in elkaar past om elk gewenst oppervlak te bedekken. Als je geïnteresseerd bent in een dergelijk gebruik, raden we je de vloerbedekking calculator 🇺🇸 en de vierkante voeten calculator 🇺🇸 aan, omdat dit uitstekende hulpmiddelen zijn voor dit doel.

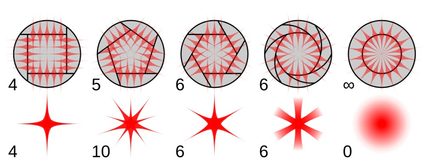
Het volgende geval geldt voor alle veelhoeken, maar is toch interessant om te zien. Bij fotografie heeft de opening van de sensor bijna altijd een veelhoekige vorm. Dit deel van de camera wordt het diafragma genoemd en dicteert veel eigenschappen en kenmerken van de foto's die een camera produceert. De meest onverwachte is de vorm van zeer heldere (puntvormige) objecten als gevolg van het effect dat diffractierooster heet, en dat wordt geïllustreerd in de afbeelding hierboven.

Een van de meest waardevolle toepassingen van zeshoeken in de moderne tijd, nauw verwant aan het gebruik in de fotografie, is in de sterrenkunde. Een van de grootste problemen die we ervaren bij het observeren van verre sterren is hoe zwak ze zijn aan de nachtelijke hemel. Dat komt omdat ze, ondanks dat het zeer heldere objecten zijn, zo ver weg staan dat slechts een klein deel van hun licht ons bereikt; je kunt daar meer over leren in onze lichtsterkte calculator 🇺🇸. Bovendien komt hun licht door relativistische effecten (vergelijkbaar met tijddilatatie en lengtesamentrekking) met minder energie op de aarde aan dan het werd uitgezonden. Dit effect wordt de roodverschuiving genoemd.

Het resultaat is dat we een kleine hoeveelheid energie krijgen met een langere golflengte dan we zouden willen. De beste manier om dit tegen te gaan is om telescopen te bouwen die zo enorm groot mogelijk zijn. Het probleem is dat het bijna onmogelijk is om een lens of spiegel uit één stuk te maken die groter is dan een paar meter, om nog maar te zwijgen over de logistieke problemen. De oplossing is om een modulaire spiegel te bouwen met zeshoekige tegels zoals je op de foto's hierboven kunt zien.

Het maken van zo'n grote spiegel verbetert de hoekresolutie van de telescoop, evenals de vergrotingsfactor dankzij de geometrische eigenschappen van een "Cassegrain telescoop". We kunnen dus zeggen dat we dankzij regelmatige zeshoeken beter, verder en duidelijker kunnen zien dan we ooit hadden kunnen doen met alleen lenzen of spiegels uit één stuk.

Wist je dat hexagon dekens ook een ding zijn? Ontdek meer met de hexagon deken calculator 🇺🇸 van Omni!

Het honingraatpatroon bestaat uit regelmatige zeshoeken die naast elkaar zijn geplaatst. Ze vullen het hele oppervlak dat ze overspannen volledig, dus er zitten geen gaten tussen. Dit honingraatpatroon komt niet alleen voor in honingraten (verrassing!) maar ook op veel andere plaatsen in de natuur. Het is zelfs zo populair dat je zou kunnen zeggen dat het de standaardvorm is als er tegenstrijdige krachten spelen en bollen niet mogelijk zijn vanwege de aard van het probleem.

Van 'bijenkorven' tot rotsspleten en organische chemie (zelfs in de bouwstenen van het leven: eiwitten), regelmatige zeshoeken zijn de meest voorkomende veelhoekige vorm in de natuur. En daar is een reden voor: de zeshoekige hoeken. De hoek van 120º is de meest mechanisch stabiele van allemaal, en toevallig is dat ook de hoek waarbij de zijden elkaar ontmoeten op de hoekpunten als we zeshoeken naast elkaar leggen. Voor een volledige beschrijving van het belang en de voordelen van regelmatige zeshoeken raden we aan deze video. te bekijken.

De manier waarop hoeken van 120º krachten (en dus spanning) verdelen over 2 van de zijden van de zeshoek, maakt het een zeer stabiele en mechanisch efficiënte geometrie. Dit is een belangrijk voordeel dat zeshoeken hebben. Een andere belangrijke eigenschap van regelmatige zeshoeken is dat ze een oppervlak kunnen vullen zonder tussenruimtes (samen met regelmatige driehoeken en vierkanten). Bovendien heeft de regelmatige zeshoek de kleinste omtrek voor de grootste oppervlakte van deze oppervlakte-vullende veelhoeken, waardoor deze zeer efficiënt is.

Een fascinerend voorbeeld in deze video is dat van de zeepbellen. Als je een zeepbel creëert met water, zeep en wat van je eigen adem, heeft deze altijd een bolvorm. Dit resultaat komt doordat het volume van een bol het grootste is van alle andere voorwerpen bij een gegeven oppervlakte.

Als we de bellen echter samen op een plat oppervlak leggen, verliest de bol zijn efficiëntievoordeel omdat de doorsnede van een bol een 2D-ruimte niet volledig kan bedekken. De op één na beste vorm qua verhouding tussen volume en oppervlak is toevallig ook het beste in het in evenwicht houden van de spanning tussen de bellen die aan het oppervlak van de bellen ontstaat. We hebben het hier natuurlijk over onze almachtige zeshoek.

Bellen zijn een interessante manier om de voordelen van een zeshoek ten opzichte van andere vormen te visualiseren, maar het is niet de enige manier. In de natuur zijn er, zoals we al zeiden, veel voorbeelden van zeshoekige formaties, meestal als gevolg van stress en spanningen in het materiaal. We kunnen ze helaas niet allemaal in detail bespreken. We kunnen echter wel een paar plaatsen noemen waar je regelmatige zeshoekige patronen in de natuur kunt vinden:

• Honingraten;
• Organische verbindingen;
• Stapels bellen;
• Rotsformaties (zoals Giant's);
• Ogen van insecten;
• ...