Diagonaal van een rechthoek berekenen

Onze diagonaal van een rechthoek calculator is een uitgebreide tool die snel de diagonaal en andere parameters van een rechthoek vindt. Heb je een specifiek probleem met betrekking to een rechthoek en weet je niet hoe je de diagonaal van een rechthoek moet vinden? Probeer een paar parameters in te voeren in de velden naast de tekst of lees verder om erachter te komen wat de mogelijke diagonaal van een rechthoek formules zijn.

In de afbeelding hieronder zie je een typische rechthoek. We hebben vijf basisgrootheden gemarkeerd die een specifieke rechthoek beschrijven. Je kunt ze gebruiken om de formule voor een diagonaal van een rechthoek af te leiden. Dit zijn:

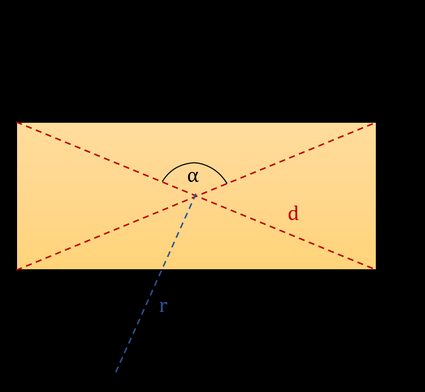
• l - Lengte;
• w - Breedte;
• a - De hoek tussen diagonalen;
• r - Cirkelstraal;
• d - Diagonaal;

en twee andere parameters die niet in de afbeelding worden getoond:

• A - Oppervlakte; en
• P - Omtrek.

De term rechthoek komt van het Latijnse rectangulus, wat een combinatie is van twee woorden: rectus (recht, juist) en angulus (hoek). Deze naam is afgeleid van het feit dat een rechthoek een vierkant is met vier rechte hoeken (4 × 90° = 360°). De overstaande zijden zijn evenwijdig en even lang, en de twee diagonalen snijden elkaar in het midden en zijn ook even lang.

Een vierkant is een speciaal geval van een rechthoek. De definitie is dat alle vier de zijden even lang zijn en dat de hoek tussen twee diagonalen recht is. Probeer onze calculators voor vierkanten, bijvoorbeeld de vierkant calculator 🇺🇸. Hiermee kun je snel de omtrek, oppervlakte en diagonaal schatten van elk vierkant dat je maar wilt, gewoon op basis van de lengte van de zijde.

Het middelpunt van een rechthoek ligt op gelijke afstand van de hoekpunten; daarom kun je er altijd een cirkel omheen omschrijven. Aan de andere kant kun je een cirkel alleen in een rechthoek omschrijven als deze een vierkant is.

Om de diagonaal van een rechthoek te bepalen, moet je:

1. De zijden van de rechthoek noteren, die we aanduiden met w en l.
2. Deze twee waarden kwadrateren. Dat wil zeggen, bereken l² en w².
3. Tel de twee gekwadrateerde waarden uit stap 2 bij elkaar op.
4. Neem de vierkantswortel van de uitkomst.
5. Dat is alles! Je hebt zojuist de lengte van de diagonaal van je rechthoek gevonden.

Waarom werkt deze procedure?

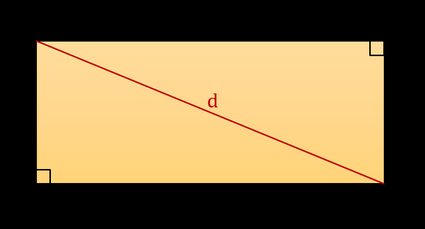
Om de hierboven gebruikte formule voor de diagonaal van een rechthoek af te leiden, verdeel je een rechthoek in twee congruente rechthoekige driehoeken, dat wil zeggen driehoeken met één hoek van 90°. Elke driehoek heeft zijden met een lengte l en w en een schuine zijde met lengte d. Je kunt de hypotenusa formule gebruiken, bijvoorbeeld uit de stelling van Pythagoras calculator 🇺🇸, om de diagonaal van een rechthoek te schatten, die kan worden uitgedrukt met de volgende formule:

d² = l² + w²

en nu zou je moeten weten hoe je de diagonaal van een rechthoek expliciet kunt berekenen - neem gewoon een vierkantswortel:

d = √(l² + w²)

Met onze diagonaal van een rechthoek calculator kun je bijna alle eenheden gebruiken die je maar wilt. Bekijk onze lengte converter 🇺🇸 of oppervlakte converter 🇺🇸 om te zien hoe je kunt wisselen tussen verschillende eenheden (SI en imperiaal).

Soms weet je de lengte van twee aangrenzende zijden van een rechthoek niet. Hoe bereken je dan de diagonaal van een rechthoek? Het antwoord vind je met onze diagonaal van een rechthoek calculator. Laten we eerst drie basisvergelijkingen opschrijven voor de oppervlakte, omtrek en straal van de omgeschreven cirkel:

1. Oppervlakte van een rechthoek: A = w × l.
2. Omtrek van een rechthoek: P = 2 × w + 2 × l.
3. Straal van de omgeschreven cirkel van een rechthoek r = d/2.

Met de bovenstaande vergelijkingen kunnen we nu verschillende formules voor diagonaal van een rechthoek afleiden die gebruikt worden door deze diagonaal van een rechthoek calculator:

1. Aan de hand van lengte en breedte:

   d = √(l² + w²)

2. Aan de hand van lengte/breedte en oppervlakte:

   d = √(A²/l² + l²) of d = √(A²/w² + w²)

3. Aan de hand van lengte/breedte en omtrek:

   d = √(2l² - P × l + P²/4)) of d = √(2w² - P × w + P²/4)

4. Aan de hand van lengte/breedte en hoek:

   d = w / sin(α/2) of d = l / cos(α/2)

5. Aan de hand van oppervlakte en omtrek:

   d = ½√(P² - 8 × A)

6. Aan de hand van oppervlakte en hoek:

   d = √(2 × A / sin(α))

7. Aan de hand van omtrek en hoek:

   d = P / (2 × sin(α/2) + 2 × cos(α/2))

8. Aan de hand van straal van de omgeschreven cirkel:

   d = 2 × r

Opmerking: De hoek α tussen diagonalen is tegenover de zijde met lengte l, zoals in de eerste afbeelding. Bedenk ook dat de diagonaal van een rechthoek calculator ervan uitgaat dat de lengte langer is dan de breedte!

Wist je dat er een speciale rechthoek bestaat die de gulden rechthoek wordt genoemd? Zo niet, ga dan naar onze gulden rechthoek calculator 🇺🇸 om te leren hoe je gulden rechthoeken kunt construeren!