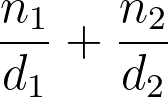Breuken berekenen

Welkom bij onze calculator om breuken te berekenen, een echt veelzijdig hulpmiddel. Het kan:

• ➕ optellen;
• ➖ aftrekken;
• ✖️ vermenigvuldigen; en
• ➗ delen van twee breuken.

Bovendien kan het een breuk vereenvoudigen (ook wel verkleinen) en je vertellen hoe je een breuk in een decimaal kunt veranderen en andersom. Als je nog niet onder de indruk bent, deze tool werkt niet alleen met standaard echte en onechte breuken, maar ook met gemengde breuken - wat wil je nog meer? 😁

Zoals gebruikelijk hebben we wat inleidende lectuur voorbereid, waarmee je je kunt verdiepen in de wereld van breuken 🌎. Hieronder lees je over de definitie van breuken, de soorten breuken (echt, onecht, gemengd) en al die basisbewerkingen op enkelvoudige en gemengde breuken. Ben je er klaar voor?

Een breuk staat voor het aantal gelijke delen van een geheel.
Je kunt een eenvoudige breuk herkennen doordat er twee getallen in staan, gescheiden door een streep (of schuine streep):

• Het bovenste getal noemen we de teller en schrijven we boven de streep. Het vertelt ons:

  Hoeveel delen we hebben.

• Het onderste getal noemen we noemer en schrijven we onder de streep. Het betekent:

  Het totale aantal onderdelen.

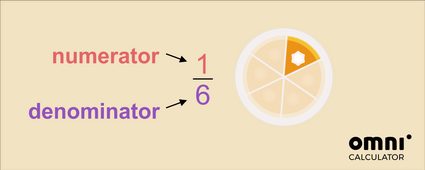
In het voorbeeld hierboven is het één deel van de zes stukken, waarin de taart in totaal is gesneden. We lezen het als een zesde van de hele taart.

Maar de taart kan natuurlijk ook anders worden gesneden!

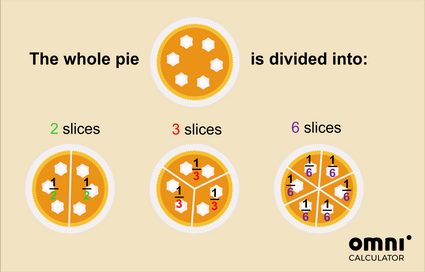
Dus, als je de taart in tweeën snijdt, dan is één stuk de helft van de hele taart. Als je de taart in 3 stukken snijdt, dan is één stuk een derde van de hele taart, enz.

Breuken worden overal om ons heen gebruikt:

• Telkens als je een deel van een heel voorwerp wilt uitdrukken, dat je in even stukken kunt verdelen: zoals een taart 🍰, een chocoladereep 🍫, een watermeloen 🍉, een pizza 🍕, enz;

• Wanneer we iets meten 📏, vooral in centimeters of een achtste van een centimeter; en

• De grootte van je computerscherm 🖥️ wordt uitgedrukt als een verhouding, bijvoorbeeld 16:9 - het is ook een breuk, alleen op een andere manier geschreven. (Kijk voor informatie over het vereenvoudigen van verhoudingen op onze verhouding calculator 🇺🇸!

Nu je de definitie van breuken kent, gaan we eens kijken naar de verschillende soorten breuken. In het algemeen hebben we drie soorten breuken: echte, onechte en gemengde breuken:

1. Echte breuken

   Bij echte breuken is het bovenste getal (teller) kleiner dan het onderste getal (noemer). Dit betekent dat het altijd kleiner is dan een geheel getal, bijv:

   🍰 5 stukken taart van een taart die in 6 is gesneden;

   🍫 2 rijen van een chocoladereep van de hele chocoladereep, die 5 rijen heeft; en

   🍊 7 stukjes van een sinaasappel van de hele sinaasappel die we in 8 hebben gesneden.

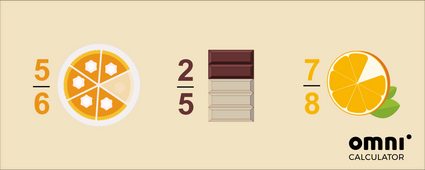
De algemene regel, die zowel voor positieve als negatieve getallen geldt, is dat de absolute waarde van een echte breuk kleiner is dan één:

2. Onechte breuken

   Wat is een onechte breuk? Het is een breuk waarbij de teller groter is dan (of gelijk is aan) de noemer. Voorbeelden van oneigenlijke breuken zijn:

   🍰 10 stukken taart, terwijl elke taart 6 stukken heeft;

   🍫 8 rijen van een chocoladereep. Een hele chocoladereep heeft 5 rijen; en

   🍊 21 stukjes sinaasappel, als we elke sinaasappel in 8 gelijke stukjes snijden.

3. Gemengde breuken

   Gemengde breuken, ook wel gemengde getallen genoemd, zijn een andere manier om een onechte breuk uit te drukken. Het zijn hele getallen (het aantal hele dingen) en een echte breuk bij elkaar. We bekijken dus de voorbeelden uit de vorige paragraaf:

   🍰 10 stukken taart, als elke taart 6 stukken heeft is hetzelfde als → 1 hele taart en 4 stukken van de 6;

   🍫 8 rijen chocolade, wanneer de hele chocoladereep 5 rijen heeft → 1 hele chocoladereep en 3 rijen van de 5; en

   🍊 21 stukjes sinaasappel, als we de sinaasappel in 8 stukjes snijden → 2 hele sinaasappels en vijf stukjes van de 8.

Bij het optellen van breuken zijn er drie scenario's:

1. De noemer (onderste getal) is hetzelfde in beide breuken - bijvoorbeeld ³/₅ en ¹/₅

   Dit is het meest eenvoudige geval; het enige wat je hoeft te doen is de tellers (bovenste getallen) bij elkaar optellen en de noemer zo laten, bijv:

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅

2. De breuken hebben ongelijke noemers - bijvoorbeeld ²/₅ en ³/₁₀

   Dit is een iets ingewikkelder geval - om deze breuken op te tellen, moet je de gemeenschappelijke noemer vinden.

   • Je kunt bijvoorbeeld KGV - het kleinste gemene veelvoud - gebruiken om het gemeenschappelijke getal van je twee noemers te vinden: KGV(5,10) = 10 Een andere optie is om je noemers te vermenigvuldigen en de breuk later te verkleinen.

   • Vervolgens moet je elke breuk zo uitzetten dat deze gemeenschappelijke noemer het onderste getal is:

   Dus, je moet de breuk met de noemer gelijk aan 5 (onze 1/5) vermenigvuldigen met 2 om 10 te krijgen (vergeet niet dat je zowel het bovenste als het onderste getal moet vermenigvuldigen):

   ➽ ²/₅ = ^{(2 × 2)}/_{(5 × 2)} = ⁴/₁₀

   De noemer van je tweede breuk is al gelijk aan 10:

   ➽ ³/₁₀

   • Nu je breuken dezelfde noemer hebben, kun je ze optellen:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀

3. Je wilt twee gemengde breuken optellen - bijvoorbeeld 2 ³/₅ en 1 ¹/₂

   Een oplossing voor dit soort problemen is om de gemengde breuk om te zetten naar een onechte breuk en deze op de gebruikelijke manier bij elkaar op te tellen.

   Laten we het omrekenen voor 2 ^{^}/₅

   • Vermenigvuldig het gehele getal met de noemer:

     2 × 5 = 10

   • Tel het resultaat op bij je teller:

     10 + 3 = 13

   • Dat is je nieuwe teller - schrijf deze bovenop je noemer:

     2 ³/₅ = ¹³/₅

   Analoog kun je uitvinden dat 1 ^{^}/₂ = ³/₂.

   • Doe de standaard optelling van breuken met oneven noemers:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀

   • Tot slot kun je je resultaat weer omzetten in een gemengde breuk:

     Doe een lange deling met een restgetal:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀

Natuurlijk kan onze breuken calculator al deze scenario's aan. 😎

Als je je nog steeds afvraagt hoe het optellen van breuken werkt, kan deze afbeelding je misschien helpen?

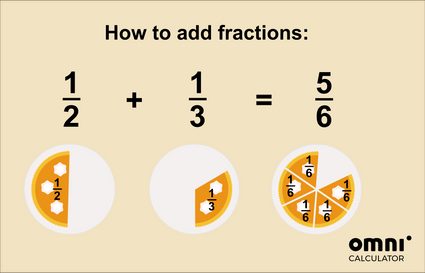
Voor een nog grondigere uitleg kun je onze breuken optellen calculator 🇺🇸 bekijken.

Als je je afvraagt hoe je breuken kunt aftrekken en je hebt de vorige paragraaf Hoe kun je breuken optellen doorgelezen, dan hebben we goed nieuws voor je: het is vrijwel hetzelfde!

1. Als je breuken hebt met dezelfde noemer, trek dan de tellers van elkaar af:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅

2. Bij het aftrekken van breuken met ongelijksoortige noemers - ²/₅ en ³/₁₀ - herhaal je de procedure uit de vorige paragraaf, maar in de laatste stap trek je af en tel je niet op:

   • Zoek een gemeenschappelijke noemer - het is 10.

   • Breid de breuken uit naar hun equivalente breuken met een gemeenschappelijke noemer: ⁴/₁₀ en ³/₁₀.

   • Trek de tellers van elkaar af.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀

3. Voor gemengde breuken (2^{^}/₅ en 1 ¹/₂):

   • Verander de gemengde breuken in onechte breuken, zoals eerder:

     2 ³/₅ = ¹³/₅ en 1 ¹/₂ = ³/₂

   • Trek de twee oneigenlijke breuken met ongelijke noemers van elkaar af:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀

   • Laat het in een onechte breuk staan, of zet het terug naar een gemengde breuk:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀

Je kunt aftrekken vergelijken met het nemen of opeten van een stuk van de taart:

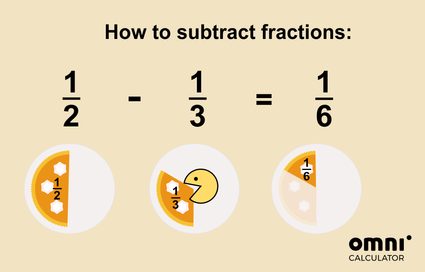
Dat was toch niet zo moeilijk, of wel?

Het vermenigvuldigen van breuken gaat - gelukkig - moeiteloos. Het is teller maal teller over noemer maal noemer. Soms moet je de breuk ook vereenvoudigen. En dat is het!

Kijk eens naar dit voorbeeld:

➽ ²/₃ × ⁵/₆ = ^{(2 × 5)}/_{(3 × 6)} = ¹⁰/₁₈

wat je dan kunt vereenvoudigen tot ⁵/₉

Wanneer je te maken hebt met gemengde breuken, vergeet dan niet dat je ze altijd moet schrijven als een onechte breuk voordat je gaat vermenigvuldigen:

➽ 2 ¹/₂ × 3 ¹/₄ = ⁵/₂ × ¹³/₄ = ^{(5 × 13)}/_{(2 × 4)} = ⁶⁵/₈ = 8 ¹/₈

En als je een breuk vermenigvuldigt met een geheel getal, onthoud dan dat je het gehele getal kunt schrijven als zichzelf gedeeld door 1:

➽ 3 × ⁵/₇ = ³/₁ × ⁵/₇ = ^{(3 × 5)}/_{(1 × 7)} = ¹⁵/₇

Als je niet weet hoe je breuken moet verkleinen, scrol dan naar beneden naar de paragraaf Hoe kun je breuken vereenvoudigen.

Nu je weet hoe je breuken kunt vermenigvuldigen, gaan we verder met het volgende onderwerp, het delen van breuken.

Zit je te piekeren over hoe je breuken kunt delen? Maak je geen zorgen! Het delen van breuken lijkt veel op het vermenigvuldigen van breuken. Het enige verschil is dat je het eerste getal moet vermenigvuldigen met de herleidbare van de tweede breuk. Het klinkt misschien een beetje raar, maar het is heel eenvoudig! Kijk eens naar dit voorbeeld:

(¹/₂) / (³/₅) = ¹/₂ × ⁵/₃ = ^{(1 × 5)}/_{(2 × 3)} = ⁵/₆

Het enige wat je dus hoeft te doen is de tweede breuk omkeren (wat de herleidbare is) en de breuken met elkaar vermenigvuldigen. Soms moet je ook wat breuken verkleinen. En dat is alles, fluitje van een cent! 🎉

We maken ons leven altijd graag eenvoudiger - zelfs in wiskunde. Daarom is het vereenvoudigen van breuken zo belangrijk. Het betekent dat we de breuk in zijn eenvoudigst mogelijke vorm schrijven. We noemen het vereenvoudigen van breuken ook wel het verminderen van breuken.

Maar wat betekent dit precies? Kijk maar eens naar deze voorbeelden:

• Je zegt toch liever dat er een vierde (een kwart) van de pizza over is in plaats van twee-achtste, nietwaar?
• of dat de helft van een taart is opgegeten, niet drie-zesde

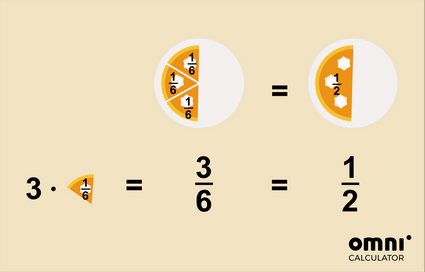
Om een breuk te vereenvoudigen kun je twee methoden gebruiken:

1. Gebruik een soort brute kracht aanpak: deel de breuk door 2, 3, 5, 7, 11... totdat het onmogelijk is om verder te delen (zonder restgetal):

   ➽ ⁴²/₁₂₆ = (21 × 2)/(63 × 2) = 21/63

   ➽ ²¹/₆₃ = (7 × 3)/(21 × 3) = 7/21

   ➽ ⁷/₂₁ = (1 × 7)/(3 × 7) = 1/3

   ➽ ¹/₃

2. Vind de GGD - grootste gemene deler van de teller en noemer, en deel ze dan door dit getal: GGD(42,126) = 42, dus

   ➽ ⁴²/₁₂₆ = (1 × 42)/(3 × 42) = 1/3

   ➽ ¹/₃

Lees meer over het verminderen van breuken in onze speciale breuken vereenvoudigen calculator 🇺🇸. Kijk ook eens naar onze geweldige gelijke breuken calculator 🇺🇸, die veel equivalenten voor jouw breuk kan vinden.

Als je wilt weten hoe je een decimaal in een breuk omzet 🇺🇸, dan zit je hier goed. Hier is een stap-voor-stap handleiding:

Laten we aannemen dat je 0,32 wilt omzetten naar een breuk:

1. Behandel je decimaal als een teller. De noemer wordt dan 1.

2. Verplaats het decimaalteken naar rechts, tot je alleen nog een geheel getal overhoudt:

   0.32 → 3.2 → 32

   Elke beweging komt overeen met een vermenigvuldiging met 10

   0.32 × 10 → 3.2 × 10 → 32

3. Je hebt de teller vermenigvuldigd met 10 × 10, en nu moeten we de noemer vermenigvuldigen met hetzelfde getal:

   1 × 10 × 10 = 100

4. Je hebt je breuk veranderd in een decimaal getal! ✨ 0.32 → ³²/₁₀₀

5. Tenslotte vereenvoudig het resultaat. Aangezien de grootste gemene deler voor 32 en 100 4 is, deel je zowel de teller als de noemer door deze waarde:

   ➽ ³²/₁₀₀ = ⁸/₂₅

En dat is alles de breuk in zijn eenvoudigste vorm. ❤️

De eenvoudigste manier om een breuk om te zetten in een decimaal is... door een calculator te gebruiken. Of het nu deze breuken calculator is, een standaard zakrekenmachine of ons speciale hulpmiddel - de breuk naar decimaal converter 🇺🇸.

Soms is een breuk relatief eenvoudig om te zetten in decimalen zonder hulpmiddelen - zoals voor 1/2, 3/4 (of zelfs 1/8). We denken dat je wel kunt bedenken hoe je de bovenstaande breuken kunt uitbreiden tot respectievelijk 10, 100, 1000, enzovoort in de noemer:

• Vermenigvuldig ¹/₂ met 5 om 10 als noemer te krijgen:

  ➽ ¹/₂ = ⁵/₁₀ = 0.5

• Vermenigvuldig ³/₄ met 25 om 100 als noemer te krijgen:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0.75

• Vermenigvuldig ¹/₈ met 125 om 1000 als noemer te krijgen:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0.125

Maar wat als je geen internet of calculator bij je hebt, maar alleen pen en papier📝? En jouw breuk lijkt niet zo makkelijk uit te breiden als de bovenstaande breuk? Dan zul je de lange deling tot achter de komma waarschijnlijk met de hand moeten doen. Veel succes! 🤞