Tankvolume berekenen

Q: Hoe bereken je het volume van een watertank?

Je kunt de Omni Calculator tool tankvolume calculator proberen of het volgende doen: Bepaal de binnenstraal en de hoogte van de tank . kwadrateer de straal en vermenigvuldig dit vervolgens met pi (3,14159...). Gefeliciteerd, je hebt de oppervlakte van de watertank. Vermenigvuldig het resultaat met de hoogte en je krijgt het tankvolume .

Q: Hoe bereken ik de capaciteit van mijn motor?

Auto-experts noemen dit de cilinderinhoud en je kunt deze als volgt berekenen: Bereken het volume van een van de cilinders van je motor. Je kunt de tankvolume calculator van Omni Calculator proberen of de straal en hoogte van de cilinder (zuigerslag van de motor) opvragen. kwadrateer de straal, vermenigvuldig met pi (3,14159...) en vervolgens met de zuigerslag. Vermenigvuldig het volume van één cilinder met het aantal cilinders in je motor en je krijgt de cilinderinhoud.

Q: Hoe lang kan opgeslagen water in een tank blijven?

Dit hangt af van de hoeveelheid water die je hebt opgeslagen en de uitstroomsnelheid. Bereken het volume van je watertank met de Omni Calculator tool tankvolume calculator. Bereken de waarde in liters. Bepaal hoeveel liter je per dag verbruikt . Deel de hoeveelheid water die je hebt door je dagelijkse verbruik. Het resultaat is hoeveel waterdagen je hebt.

Q: Waarom geven we de voorkeur aan cilindrische watertanks in plaats van vierkante?

Er zijn twee belangrijke redenen waarom we cilindrische tanks verkiezen boven rechthoekige tanks: Cilindrische tanks zijn beter bestand tegen spanning dan rechthoekige tanks. Fabrikanten hebben dus minder materiaal nodig om ze te bouwen. Rechthoekige tanks zijn moeilijker schoon te maken , vooral in de hoeken.

Q: Wat is het volume van een olievat?

218,7 liter. Een olievat heeft een diameter van 0,572 m en een hoogte van 0,851 m. Voer deze cijfers in de volgende formule in: Volume = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 liter

Makers

Hanna Pamuła, PhD

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Vertalers

Catherina Vandenbroecke

Beoordelaars

Bogna Szyk

Bogna is the chief operating officer at Omni Calculator, where she helps keep things running smoothly and ideas moving forward. With a background in civil engineering and a knack for organizing chaos, she brings structure and strategy to everything she does. After hours, you’ll likely find her dancing zouk or crafting the next twist in a D&D campaign. See full profile

Check our editorial policy

en Jack Bowater

Met deze tankvolume calculator kun je eenvoudig het volume van je container schatten. Kies uit tien verschillende tankvormen: van standaard rechthoekige en cilindrische tanks tot capsule- en elliptische tanks. Je kunt zelfs het volume van een afgeknotte kegel berekenen in tanks met een kegelbodem. Voer gewoon de afmetingen van je tank in en dit hulpmiddel berekent het totale tankvolume voor je. Je kunt ook de vulhoogte opgeven, die wordt gebruikt om het gevulde volume te vinden.

Vraag je je af hoe het werkt? Scrol naar beneden en je vindt alle formules die je nodig hebt - het volume van een capsule tank, elliptische tank of de veelgebruikte kegelbodemtanks (ook wel conische tanks genoemd), en nog veel meer!

Ben je op zoek naar andere soorten tanks in verschillende vormen en voor andere toepassingen? Bekijk onze volume calculator om het volume van de meest voorkomende driedimensionale vaste stoffen te vinden. Voor iets meer gespecialiseerd kun je ook een kijkje nemen bij de aquarium calculator 🇺🇸 en zwembad volume calculators 🇺🇸 voor oplossingen voor alledaagse volumeproblemen.

Hoe kun je de tankvolume calculator gebruiken

Deze tankvolume calculator is een eenvoudig hulpmiddel waarmee je zowel het volume van de tank als het volume van het gevulde deel kunt vinden. Je kunt kiezen uit tien tankvormen:

Verticale cilinder;
Horizontale cilinder;
Rechthoekig prisma (doos);
Verticale capsule;
Horizontale capsule;
Verticaal ovaal (elliptisch);
Horizontaal ovaal (elliptisch);
Kegelbodem;
Kegel top; en
Afgeknotte kegel (trechtervormig)

"Maar hoe gebruik ik deze tankvolume calculator?", vraag je je misschien af. Laten we eens kijken naar een eenvoudig voorbeeld:

Bepaal de vorm. Laten we aannemen dat we het volume van een verticale cilindertank willen vinden - kies die optie in het keuzemenu. De schematische afbeelding van de tank verschijnt hieronder; controleer of dit de tank is die je wilt!
Voer de afmetingen van de tank in. In ons geval moeten we de lengte en diameter invoeren. In ons voorbeeld zijn die respectievelijk $32\ \mathrm{cm}$ en $24\ \mathrm{cm}$ . Daarnaast kunnen we de gevulde hoogte invoeren - $28\ \mathrm{cm}$ .
De tankvolume calculator heeft het totale en gevulde volume al berekend! Het totale volume van de tank is $14,48\ \mathrm{L}$ en het volume van de vloeistof erin is $12,67\ \mathrm{L}$ . Zoals altijd kun je de eenheden wijzigen door op de volume-eenheden zelf te klikken. Een fluitje van een cent!

Volumeformule voor cilindrische tank

Om het totale volume van een cilindrische tank te berekenen, hoeven we alleen maar de cilinderdiameter (of straal) en de cilinderhoogte (die lengte kan worden genoemd als deze horizontaal ligt) te weten.

Verticale cilindertank

We kunnen het totale volume van een cilindrische tank vinden met de standaardformule voor volume - de oppervlakte van de basis vermenigvuldigd met de hoogte. Een cirkel is de vorm van de basis, dus de oppervlakte is, volgens de bekende vergelijking, gelijk aan $\pi \times \mathrm{radius}^2$ . Daarom ziet de formule voor het volume van een verticale cilindertank er als volgt uit:

\begin{split} V_{\scriptsize{\mathrm{\tiny verticale\ cilinder}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h, \end{split}

waarbij:

$r$ - Straal van de basis; en
$h$ - Hoogte van de cilinder.

Als we het gevulde volume willen berekenen, moeten we het volume van een "kortere" cilinder berekenen - zo eenvoudig is het!

\begin{split} V_{\scriptsize{\mathrm{\tiny verticale\ cilinder}}} &= \pi \times r^2 \times f\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times f, \end{split}

waarbij $f$ de hoogte is van het gevulde deel van de cilinder.

Horizontale cilindertank

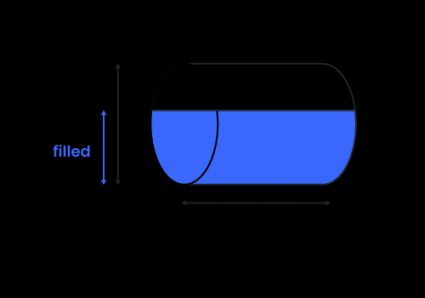
Het totale volume van een horizontale cilindrische tank kan op een analoge manier worden gevonden - het is de oppervlakte van het ronde uiteinde maal de lengte van de cilinder:

\begin{split} V_{\scriptsize{\mathrm{\tiny horizontale\ cilinder}}} &= \pi \times r^2 \times l\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times l, \end{split}

waarbij $l$ de lengte van de cilinder is.

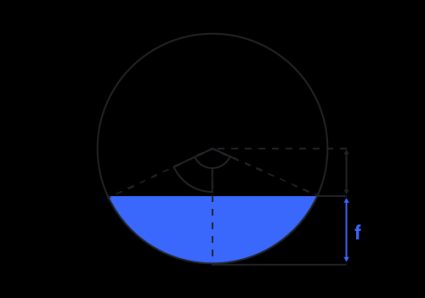
Dwarsdoorsnede van een gedeeltelijk gevulde cilindrische tank.

De dingen worden ingewikkelder als we het volume van de gedeeltelijk gevulde horizontale cilinder willen berekenen. Eerst moeten we de basisoppervlakte berekenen: de oppervlakte van het cirkelsegment dat door de vloeistof wordt bedekt:

A_{\mathrm{\tiny segment}} = \frac{1}{2} \times r^2 \times (\theta-\sin(\theta)),

waarbij $r$ de straal van de basis is en $\theta$ de centrale hoek van het segment. De hoek $\theta$ kan worden gevonden met de formule voor cosinus:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f},

waarbij $f$ de hoogte is van het gevulde deel van de basis.

Daarom:

\theta= 2\times \arccos\left(\frac{r-f}{f}\right)

En tot slot is de formule voor het volume van een gedeeltelijk gevulde horizontale cilinder $V_{\scriptsize{\mathrm{fhc}}}$ :

\small V_{\scriptsize{\mathrm{fhc}}} = 0,5\times r^2\times(\theta -\sin(\theta))\times l,

waarbij:

\theta = 2\times \arccos\left(\frac{r-f}{r}\right)

Als de cilinder meer dan halfvol is, dan is het makkelijker om het lege tankgedeelte af te trekken van het totale volume.

Volume van rechthoekige tank berekenen (rechthoekig prisma)

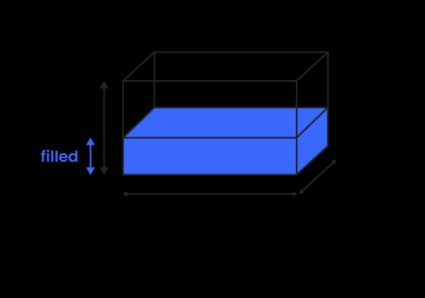
Rechthoekige tank met gemarkeerde afmetingen.

Als je je afvraagt hoe je het volume van een rechthoekige tank (ook wel kubus, doos of rechthoekige zeshoek genoemd) kunt berekenen, zoek dan niet verder! Je kent deze tank misschien als een rechthoekige tank - maar dat is niet de juiste naam, want een rechthoek is een 2D-vorm en heeft dus geen volume.

Om het volume van een rechthoekig prisma te vinden, vermenigvuldig je alle afmetingen van de tank:

V_{{\mathrm{rechthoekig\ prisma}}} = h\times b\times l,

waarbij:

$h$ - De hoogte van de tank;
$b$ - De breedte; en
$l$ - De lengte van de tank.

Als je wilt weten wat het volume van de vloeistof in een tank is, verander je gewoon de variabele hoogte in gevuld in de formule voor het volume van een rechthoekige tank. Het volume van een rechthoekig gevuld prisma, $V_{\scriptsize{\mathrm{rpf}}}$ , is:

V_{{\mathrm{rpf}}} = f\times b\times l,

waarbij $f$ de hoogte is van het gevulde gedeelte.

Voor deze tankvolume calculator maakt het niet uit of de tank horizontaal of verticaal staat. Zorg er alleen voor dat gevuld en hoogte langs dezelfde as liggen.

Formule voor volume van een capsule

Onze tool definieert een capsule als twee halve bollen gescheiden door een cilinder. Om het totale volume van een capsule te berekenen hoef je alleen maar het volume van de bol bij het cilindergedeelte op te tellen:

V_{\scriptsize{\mathrm{cap}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!l\right)

Afhankelijk van de positie van de tank zullen de berekeningen voor het gevulde volume een beetje verschillen:

1. Voor horizontale capsuletank

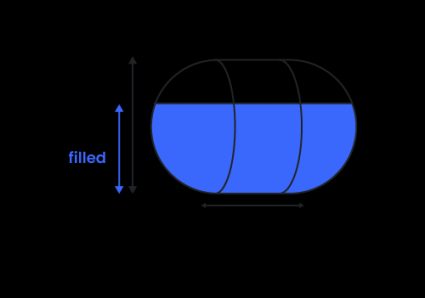
Horizontale capsuletank met gemarkeerde afmetingen.

Omdat de halve bollen aan beide uiteinden van de tank identiek zijn, vormen ze een bolvormige kap - tel dit deel $V_{\scriptsize{\mathrm{sph\ hf}}}$ op bij het deel van de horizontale cilinder $V_{\scriptsize{\mathrm{fhc}}}$ (controleer de paragraaf hierboven) om het volume van de vloeistof in een gevulde horizontale capsule te berekenen ( $V_{\scriptsize{\mathrm{cap\ hf}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{cap\ hf}}} = V_{\scriptsize{\mathrm{fhc}}}+V_{\scriptsize{\mathrm{sph\ hf}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times l \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right), \end{split}

waarbij:

$d$ - Diameter van de tank;
$f$ - Gevulde hoogte; en
$\theta$ - De hoek die overeenkomt met de gevulde sector in de cilindertank.

2. Voor verticale capsuletank

De formule verschilt voor verschillende vulhoogtes. In alle volgende formules zullen we deze grootheden tegenkomen:

$d$ - Diameter van de tank;
$f$ - Hoogte van de vloeistof; en
$l$ - Lengte van de cilindrische doorsnede.

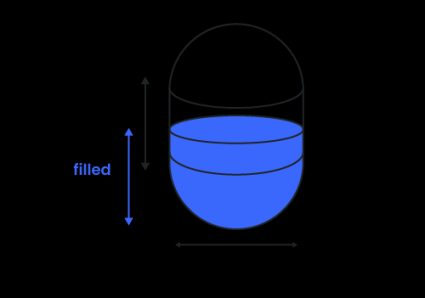
Verticale capsuletank met gemarkeerde afmetingen.

Als $f < d/2$ , dan bevindt de vloeistof zich alleen in het onderste halfronde deel, dus hebben we alleen de formule voor het volume van een bolvormige capsule nodig:

\\[2em] V_{\scriptsize{\mathrm{cap\ f}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]

Als $d/2 < f < d/2 +l$ , dan moeten we het volume van de halve bol en de "kortere" cilinder bij elkaar optellen:

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}

Als $d/2 + l < f$ , betekent dit dat we een volle onderste halve bol en cilinder hebben, dus hoeven we alleen de bolvormige capsule (lege deel) van het hele volume af te trekken:

\begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\times(l+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (l+d-f)\right) \end{split}

Volume elliptische tank (ovale tank)

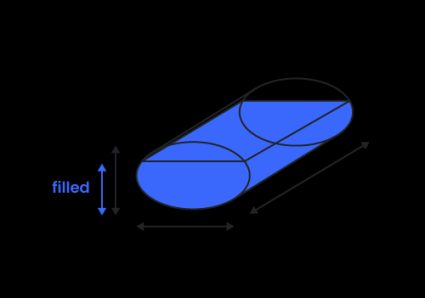
Horizontale ovale tank met gemarkeerde afmetingen.

In onze calculator definiëren we een ovale tank als een cilindrische tank met een ellipsvormig uiteinde (niet in de vorm van een stadion, zoals het soms wordt gedefinieerd). Om het totale volume van een elliptische tank te vinden, moet je het ellipsoppervlak vermenigvuldigen met de lengte van de tank:

V_{\scriptsize{\mathrm{ellips}}} = \pi\!\times\!b\!\times\!l\!\times\!\frac{h}{4},

waarbij:

$d$ - Breedte van de tank;
$h$ - hoogte van de tank; en
$l$ - Lengte van de tank.

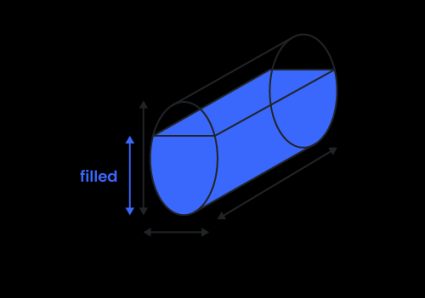
Verticale ovale tank met gemarkeerde afmetingen.

Eindelijk weer een makkelijke formule! Helaas is het berekenen van het volume van een gedeeltelijk gevulde tank - zowel in horizontale als verticale positie - niet zo eenvoudig. Je moet de formule voor de oppervlakte van het ellipssegment gebruiken en het resultaat vermenigvuldigen met de lengte van de tank:

\begin{split} &V_{\scriptsize{\mathrm{ell\ f}}} = l\!\times\!h\!\times\!\frac{b}{4}\\[1em] &\qquad\times\!\left[\arccos\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Afgeknotte kegel volume - tank in de vorm van een afgeknotte kegel

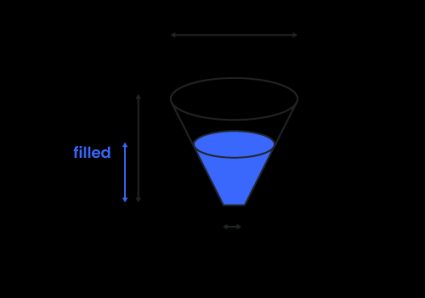
Afgeknotte tank met gemarkeerde afmetingen.

Om het volume van de afgeknotte kegel te berekenen (een bijzondere vorm die we tegenkwamen in onze afgeknotte kegel calculator 🇺🇸), gebruik je de formule:

\begin{split} &V_{\scriptsize{\mathrm{frustum}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cone}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\!+\! \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right), \end{split}

waarbij:

$d_{\mathrm{top}}$ - bovendiameter van de afgeknotte kgel;
$d_{\mathrm{bot}}$ - Onderdiameter van de afgeknotte kegel;
$h_{\mathrm{kegel}}$ - Hoogte van de tank.

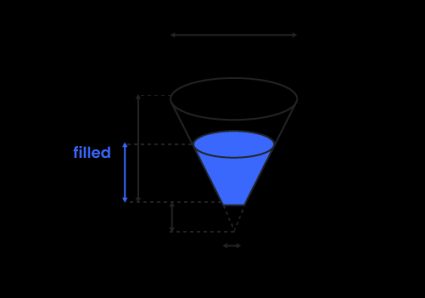
Afgeknotte tank met gemarkeerde afmetingen en vloeistofniveau.

Als je het gedeeltelijk gevulde afgeknotte volume voor een gegeven vulhoogte wilt vinden, bereken je eerst de bovenste straal van het gevulde gedeelte:

R = \frac{1}{2} \times d_{\mathrm{top}}\times \frac{f+z}{h_{\mathrm{kegel}}+z},

waarbij:

z = h_\mathrm{kegel} \times \frac{d_{\mathrm{bot}}}{d_{\mathrm{top}}-d_{\mathrm{bot}}}

(Je kunt de formule afleiden uit de gelijkenis van driehoeken)

Zoek daarna gewoon het nieuwe afgeknotte volume:

\begin{split} &V_{\scriptsize{\mathrm{ff}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{bot}}}{2} + \left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right) \end{split}

Tankvolume met kegelbodem (conische tank) en tanks met kegelbovenkant

Tank met kegelbodem en gemarkeerde afmetingen.

Het totale volume van een tank met een kegelbodem vinden is niet zo moeilijk: tel gewoon het volume van het afgeknotte deel op bij het volume van het cilindrische deel:

\begin{split} &V_{\scriptsize{\mathrm{kegel\ b}}} = V_{\scriptsize{\mathrm{afgeknotte kegel}}} + V_{\scriptsize{\mathrm{cilinder}}}\\[1em] & =\frac{1}{3}\times\pi\times h_{\mathrm{kegel}} \times\left( \left(\frac{d_{\mathrm{top}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{top}}}{2}\!\times\!\frac{d_{\mathrm{bot}}}{2}\!+\!\left(\frac{d_{\mathrm{bot}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\times\left(\frac{d_{\mathrm{top}}}{2}\right)^2\times h_{\mathrm{cilinder}}, \end{split}

waarbij:

$d_{\mathrm{top}}$ - bovendiameter van de afgeknotte kegel;
$d_{\mathrm{bot}}$ - Onderdiameter van de afgeknotte kegel;
$h_{\mathrm{kegel}}$ en $h_{\mathrm{cilinder}}$ - de hoogten van de twee tanks.

Om de gedeeltelijk gevulde tank te berekenen, hoef je alleen maar het afgeknotte kegelgedeelte en cilindergedeelte bij elkaar op te tellen, afhankelijk van het niveau van de gevulde vloeistof, met behulp van bovenstaande vergelijkingen.

Het berekenen van het totale volume van de bovenste kegeltank is exact hetzelfde als dat van de onderste kegeltank. Het enige verschil is wanneer je het gevulde deel wilt vinden – natuurlijk wordt eerst het cilindrische deel gevuld, en pas daarna de afgeknotte kegel.

🙋 Heb je al je volumes berekend met metrische eenheden, maar heb je imperiale eenheden nodig? Maak je geen zorgen, want Omni heeft een handige oplossing voor al je behoeften: gebruik onze volume conversie 🇺🇸 tool om snel te converteren tussen volume-eenheden!

Veelgestelde vragen

Hoe bereken je het volume van een watertank?

Je kunt de Omni Calculator tool tankvolume calculator proberen of het volgende doen:

Bepaal de binnenstraal en de hoogte van de tank.
kwadrateer de straal en vermenigvuldig dit vervolgens met pi (3,14159...). Gefeliciteerd, je hebt de oppervlakte van de watertank.
Vermenigvuldig het resultaat met de hoogte en je krijgt het tankvolume.

Hoe bereken ik de capaciteit van mijn motor?

Auto-experts noemen dit de cilinderinhoud en je kunt deze als volgt berekenen:

Bereken het volume van een van de cilinders van je motor. Je kunt de tankvolume calculator van Omni Calculator proberen of de straal en hoogte van de cilinder (zuigerslag van de motor) opvragen.
kwadrateer de straal, vermenigvuldig met pi (3,14159...) en vervolgens met de zuigerslag.
Vermenigvuldig het volume van één cilinder met het aantal cilinders in je motor en je krijgt de cilinderinhoud.

Hoe lang kan opgeslagen water in een tank blijven?

Dit hangt af van de hoeveelheid water die je hebt opgeslagen en de uitstroomsnelheid.

Bereken het volume van je watertank met de Omni Calculator tool tankvolume calculator. Bereken de waarde in liters.
Bepaal hoeveel liter je per dag verbruikt.
Deel de hoeveelheid water die je hebt door je dagelijkse verbruik. Het resultaat is hoeveel waterdagen je hebt.

Waarom geven we de voorkeur aan cilindrische watertanks in plaats van vierkante?

Er zijn twee belangrijke redenen waarom we cilindrische tanks verkiezen boven rechthoekige tanks:

Cilindrische tanks zijn beter bestand tegen spanning dan rechthoekige tanks. Fabrikanten hebben dus minder materiaal nodig om ze te bouwen.
Rechthoekige tanks zijn moeilijker schoon te maken, vooral in de hoeken.

Wat is het volume van een olievat?

218,7 liter. Een olievat heeft een diameter van 0,572 m en een hoogte van 0,851 m. Voer deze cijfers in de volgende formule in:

Volume = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 liter