Calcolatore di Combinazioni

Questo calcolatore di combinazioni (calcolatore di n su k) è uno strumento che ti aiuta non solo a determinare il numero di combinazioni in un insieme (spesso indicato come nCr), ma ti mostra anche ogni singola combinazione (o permutazione) possibile del tuo insieme, fino alla lunghezza di 20 elementi. Tuttavia, fai attenzione! Potrebbero essere necessari anche un paio di secondi per trovare termini così lunghi per il nostro generatore di combinazioni. Se ti chiedi quante combinazioni diverse possono essere realizzate con un determinato numero di elementi e una determinata dimensione del campione, prova subito il nostro calcolatore di combinazioni!

Se non sei ancora sicuro di cosa sia una combinazione, ti spiegheremo tutto nell'articolo seguente. Qui troverai la definizione di combinazione e la formula della combinazione (con e senza ripetizioni). Ti mostreremo come calcolare le combinazioni e cosa sono la combinazione lineare e la probabilità di combinazione. Infine, parleremo della relazione tra permutazione e combinazione. In breve, la permutazione tiene conto dell'ordine dei membri mentre la combinazione non lo fa. Puoi trovare maggiori informazioni qui sotto!

Ti sei mai chiesto quante probabilità hai di vincere il primo premio di una lotteria? Quanto è probabile vincere il secondo premio? Per rispondere a entrambe le domande e ad altre simili, è necessario utilizzare le combinazioni. Abbiamo uno strumento speciale dedicato a questo tipo di problemi. Il nostro calcolatore per la lotteria 🇺🇸 non si limita a stimare la probabilità di vincita di qualsiasi gioco del lotto, ma fornisce anche una formula per le lotterie. Provala! Scoprirai quanto sono grandi (o piccoli) questi numeri.

La definizione di combinazione dice che è il numero di modi in cui è possibile scegliere r elementi da un insieme contenente n elementi distinti (ecco perché questi problemi sono spesso chiamati "n su r"). L'ordine in cui si scelgono gli elementi non è essenziale rispetto alla permutazione (puoi trovare un'ampia spiegazione di questo problema nella sezione permutazione e combinazione).

Cercare ogni combinazione di un insieme di elementi è un problema puramente matematico. Probabilmente ti è già stato insegnato, ad esempio, come trovare il massimo comune divisore (MCD) o come trovare il minimo comune multiplo (MCM). Beh, una combinazione è una storia completamente diversa. Vediamo quanto potrebbe essere complicato.

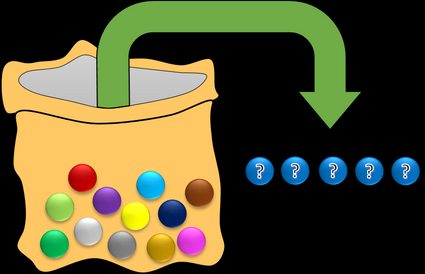
Immagina un sacchetto pieno di dodici palline, ognuna delle quali è di un colore diverso. Scegli cinque palline a caso. Quante serie distinte di palline puoi ottenere? Cioè, quante combinazioni diverse puoi ottenere?

I matematici forniscono la soluzione esatta per molti problemi, per esempio come calcolare la metratura o come calcolare il volume. Esiste un approccio simile per stimare il numero di combinazioni nell'esempio precedente con le palline?

Per fortuna non devi scrivere tutti i possibili insiemi! Come si calcolano le combinazioni, allora? Puoi utilizzare la formula seguente delle combinazioni che ti permetterà di determinare il numero di combinazioni in pochissimo tempo:

dove:

• $C(n,r)$ — Numero di combinazioni;
• $n$ — Numero totale di elementi dell'insieme; e
• $r$ — Numero di elementi scelti dall'insieme.

Il punto esclamativo $!$ rappresenta un fattoriale. Consulta il nostro calcolatore per il fattoriale 🇺🇸 per maggiori informazioni su questo argomento. L'espressione sul lato destro è nota anche come coefficiente binomiale.

Applichiamo questa equazione al nostro problema con le palline colorate. Dobbiamo determinare quante combinazioni diverse ci sono:

Puoi verificare il risultato con il nostro calcolatore di nCr. Anche in questo caso verranno elencate tutte le combinazioni possibili! Tuttavia, tieni presente che 792 combinazioni diverse sono già molte da mostrare. Per evitare che le combinazioni generate siano troppe, abbiamo limitato il generatore di combinazioni a un numero massimo specifico di combinazioni (2000 per impostazione predefinita). Puoi cambiarlo nella Modalità avanzata quando vuoi.

Puoi notare che, secondo la formula delle combinazioni, il numero di combinazioni per scegliere un solo elemento è semplicemente $n$. D'altra parte, se devi selezionare tutti gli elementi, c'è solo un modo per farlo. Verifichiamo questa proprietà di combinazione con il nostro esempio. Il numero totale di elementi è pari a $n = 12$. Ogni lettera visualizzata nel calcolatore di nCr rappresenta un colore distinto di una palla, ad esempio A è rosso, B è giallo, C è verde e così via. Se scegli un solo elemento $r = 1$ alla volta da questo insieme, il numero di combinazioni sarà $12$ — perché ci sono 12 palline diverse. Tuttavia, se scegli $r = 12$ elementi, ci sarà solo $1$ combinazione possibile che comprende tutte le palline. Prova te stesso con il calcolatore di n su r!

A questo punto, probabilmente sai tutto quello che dovresti sapere sulle combinazioni e sulla formula della combinazione. Se non ne hai ancora abbastanza, nelle prossime sezioni parleremo delle differenze tra permutazione e combinazione (che spesso vengono erroneamente considerate la stessa cosa), della probabilità di combinazione e della combinazione lineare.

Immagina di avere lo stesso sacchetto pieno di palline colorate come nell'esempio della sezione precedente. Anche in questo esempio, scegli cinque palline a caso, ma questa volta l'ordine è importante — è importante se scegli la prima o la terza pallina rossa. Facciamo un esempio più semplice in cui si scelgono tre palline chiamate R (rosso), B (blu), G (verde). Esistono sei permutazioni di questo insieme (l'ordine delle lettere determina l'ordine delle palline selezionate): RBG, RGB, BRG, BGR, GRB, GBR, e la definizione di combinazione dice che esiste una sola combinazione! Questa è la differenza cruciale.

Per definizione, una permutazione è l'atto di riorganizzazione di tutti i membri di un insieme in qualche sequenza od ordine. Tuttavia, in letteratura, spesso generalizziamo questo concetto e rinunciamo al requisito di utilizzare tutti gli elementi di un dato insieme. Questo è ciò che rende la permutazione e la combinazione così simili. Questo significato di permutazione determina il numero di modi in cui è possibile scegliere e disporre r elementi di un insieme contenente n elementi distinti. Si parla di r-permutazioni di n (talvolta chiamate variazioni). Se desideri una spiegazione ancora più approfondita, il calcolatore per la permutazione 🇺🇸 dovrebbe soddisfare questa esigenza.

La formula della permutazione è la seguente:

Questa equazione non ti sembra familiare alla formula di combinazione? Infatti, se conosci il numero di combinazioni, puoi facilmente calcolare il numero di permutazioni:

Se attivi la Modalità avanzata di questo calcolatore di combinazioni, potrai trovare il numero di permutazioni.

Potresti chiederti quando dovresti usare una permutazione invece di una combinazione. Beh, dipende dalla necessità di prendere in considerazione l'ordine o meno. Ad esempio, supponiamo che tu abbia un mazzo di nove carte con cifre da $1$ a $9$. Estrai tre carte a caso e le allinei sul tavolo, creando un numero a tre cifre, ad esempio $425$ o $837$. Quanti numeri distinti puoi creare?

Controlla il risultato con il nostro calcolatore di nCr! E quante combinazioni diverse esistono?

Il numero di combinazioni è sempre inferiore al numero di permutazioni. Questa volta è sei volte più piccolo (se moltiplichi $84$ per $3! = 6$, otterrai $504$). Ciò deriva dal fatto che ogni tre carte scelte può essere riorganizzata in sei modi diversi, proprio come nell'esempio precedente con tre palline colorate.

Per completare le nostre considerazioni su permutazione e combinazione, dobbiamo introdurre una selezione simile, ma questa volta con ripetizioni consentite. Ciò significa che ogni volta che scegli un elemento dall'insieme di n elementi distinti, lo rimetti in quell'insieme. Nell'esempio con le palline colorate, prendi una pallina dal sacchetto, ricorda quale hai pescato e rimettila nel sacchetto. Analogamente, nel secondo esempio con le carte, scegli una carta, scrivi il numero su quella carta e la rimetti nel mazzo. In questo modo, puoi avere, ad esempio, due palline rosse nella tua combinazione o 228 come permutazione.

Probabilmente immaginerai che entrambe le formule saranno molto complicate. Tuttavia, non è così sofisticato come calcolare il contenuto alcolico della tua birra fatta in casa. Infatti, nel caso della permutazione, l'equazione diventa ancora più semplice. La formula della combinazione con ripetizione è la seguente:

e per la permutazione con ripetizione:

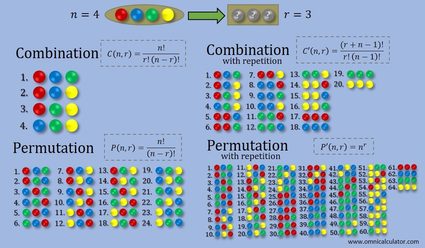
Nell'immagine che segue, presentiamo un riepilogo delle differenze tra quattro tipi di selezione di un elemento:

• Combinazione;
• Combinazione con ripetizione;
• Permutazione; e
• Permutazione con ripetizione.

Si tratta di un esempio in cui hai quattro palline di vari colori e ne scegli tre. Nel caso delle selezioni con ripetizione, puoi scegliere una delle palline più volte. Se vuoi provare con le permutazioni, fai attenzione, ci saranno migliaia di insiemi diversi! Tuttavia, puoi sempre calcolare con sicurezza quanti sono (le permutazioni sono nella Modalità avanzata).

Cominciamo con la probabilità di combinazione, un elemento essenziale in molti problemi statistici. L'esempio riportato qui sopra dovrebbe spiegarlo facilmente — scegli tre palline colorate su quattro dal sacchetto. Supponiamo che tu voglia conoscere le probabilità che tra queste ci sia una pallina rossa. Ci sono quattro combinazioni diverse e la pallina rossa è presente in tre di esse. La probabilità di combinazione è quindi:

Se estrai tre palline a caso dal sacchetto, nel 75% dei casi sceglierai una pallina rossa. Per esprimere la probabilità, di solito si usa il segno di percentuale.

Ora, supponiamo che tu prenda una pallina, scriva quale colore hai ottenuto e la rimetta nel sacchetto. Qual è la probabilità combinata di ottenere almeno una pallina rossa? Questo è un problema di 'combinazione con ripetizione'. Dall'immagine qui sopra, puoi vedere che ci sono venti combinazioni in totale e la pallina rossa è presente in dieci di esse, quindi:

È una sorpresa per te? Beh, non dovrebbe esserlo. Quando restituisci la prima pallina, ad esempio quella blu, puoi pescarla anche come seconda e terza pallina. Le probabilità di ottenere una pallina rossa sono quindi abbassate. Puoi fare considerazioni analoghe con la permutazione. Prova a risolvere un problema con il sacchetto di palline colorate: qual è la probabilità che la tua prima pallina scelta sia rossa?

Supponiamo che tu non ti fidi di noi e che voglia fare un test da solo. Estrai tre palline su quattro e controlla se c'è una pallina rossa o meno (come nel primo esempio di questa sezione). Ripeti il processo altre tre volte e ottieni la pallina rossa solo in uno dei quattro casi — $25\%$ dei casi. Secondo la teoria, ti aspettavi $75\%$. Cosa è successo? Beh, è così che funziona la probabilità! Esiste la legge dei grandi numeri che descrive il risultato dell'esecuzione dello stesso esperimento per un gran numero di volte. Se ripeti il disegno, ad esempio cento volte, ti avvicinerai molto di più a $75\%$.

Inoltre, la legge dei grandi numeri porta quasi sempre alla distribuzione normale standardizzata, che può descrivere, per esempio, l'intelligenza o l'altezza delle persone, con un cosiddetto valore p. Vuoi saperne di più? il calcolatore della distribuzione normale è il posto giusto!

Hai mai sentito parlare della combinazione lineare? In realtà, nonostante abbia la parola combinazione, non ha molto in comune con quanto abbiamo imparato finora. Tuttavia, cercheremo di spiegarla brevemente. Una combinazione lineare è il risultato di un insieme di termini e moltiplicando ogni termine per una costante e sommando i risultati. Viene spesso utilizzata nella fisica ondulatoria per prevedere l'equazione del reticolo di diffrazione o anche nella fisica quantistica grazie all'equazione di de Broglie. Qui puoi vedere alcuni esempi comuni della combinazione lineare:

1. Vettori. Ogni vettore in 3D può essere scomposto in tre vettori unitari $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ e $\^e_3 = (0,0,1)$. Ad esempio, $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ è una combinazione lineare.
2. Funzioni. Supponiamo di avere due funzioni $f(x) = \text{e}^x$ e $g(x) = \text{e}^{-x}$. Da queste due funzioni puoi creare combinazioni lineari che descrivono il seno iperbolico $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ o il coseno $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$. Puoi fare una cosa simile con il seno e il coseno normali, ma devi usare il numero immaginario $i$. Ne parliamo meglio nell'ultima sezione del calcolatore per la radice quadrata.
3. Polinomi. Per esempio, hai tre polinomi $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ e vuoi esprimere la funzione $q(x) = 2x^2 + x + 3$ come una combinazione lineare di questi polinomi. Non è sempre possibile farlo, ma in questo caso $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.

La differenza fondamentale tra combinazioni e permutazioni in matematica è l'importanza dell'ordine degli elementi:

• Nelle permutazioni, l'ordine è importante, quindi disponiamo gli elementi in ordine sequenziale, mentre

• Nelle combinazioni, l'ordine non conta, quindi selezioniamo un gruppo di elementi da una collezione più ampia.

Se hai già una combinazione e vuoi trasformarla in una permutazione, devi imporre un ordine all'insieme di elementi, cioè scegliere uno dei possibili ordinamenti per il tuo insieme. Quindi, il numero di permutazioni di r elementi scelti da n elementi è uguale al numero di combinazioni di r elementi scelti da n elementi moltiplicato per il numero di ordinamenti di questi r elementi, cioè per r!.

Se hai già una permutazione e vuoi trasformarla in una combinazione, devi rimuovere l'ordine, cioè considerare tutti i possibili riordini come lo stesso elemento. Quindi, il numero di combinazioni di r elementi scelti da n elementi è uguale al numero di permutazioni di r elementi scelti da n elementi diviso per il numero di ordinamenti di questi r elementi, cioè per r!.

Se la parola ha sette lettere distinte, hai 7! = 5040 modi di disporle (semplici permutazioni di sette elementi). Tuttavia, se alcune lettere compaiono più di una volta, il numero di disposizioni si riduce! Per esempio:

• Se la parola è "TESTIMONE", la "T" compare due volte, quindi dividiamo 7! per 2! = 2 e il risultato è 2520.

• Se la parola è "MATEMATICA", abbiamo "M" ed "T" che compaiono due volte, quindi dividiamo 7! per 2! × 2! = 4 e il risultato è 1260.

• Se la parola è "SCONOSCIUTO", abbiamo "O" tre volte, quindi dividiamo 7! per 3! = 6 e il risultato è 840.