Calcolatore della Progressione Geometrica

Created by Álvaro Díez and Anna Szczepanek, PhD

Reviewed by Bogna Szyk and Jack Bowater

Translated by Rangsimatiti Binda Saichompoo and Sara Naouar

Last updated: Oct 30, 2024

Table of contents:

Calcola tutto ciò che riguarda una progressione geometrica con il nostro calcolatore della progressione geometrica. Questo strumento a comprendere la definizione di progressione geometrica, in modo da poter rispondere alla domanda — cos'è una progressione geometrica?

Ti spiegheremo la differenza tra le due equazioni della progressione geometrica, la formula esplicita e inversa di una progressione geometrica e come utilizzare la formula della progressione geometrica con alcuni interessanti esempi di progressione geometrica.

Abbiamo anche creato una funzione "calcolatore di serie geometriche" che valuterà la somma di una progressione geometrica partendo dalla formula esplicita di una progressione geometrica e arrivando, passo dopo passo, alla formula della serie geometrica.

Definizione di progressione geometrica

La definizione di progressione geometrica è che un insieme di numeri in cui tutti, tranne il primo, si ottengono moltiplicando il precedente per un numero fisso e non nullo chiamato rapporto comune. Se non riesci a capire cosa sia la progressione geometrica, non preoccuparti! Più avanti ti spiegheremo cosa significa in termini più semplici e daremo un'occhiata alla formula inversa ed esplicita della progressione geometrica. Includiamo anche un paio di esempi di progressioni geometriche.

Prima di analizzare la definizione in modo corretto, è importante chiarire alcune cose per evitare confusione. Prima di tutto, dobbiamo capire che anche se la progressione geometrica è costituita da una costante moltiplicazione di numeri per un fattore, questo non è correlato al fattoriale (vedi calcolatore per il fattoriale 🇺🇸). Infatti, ciò a cui si riferisce è il massimo comune divisore (MCD) e minimo comune multiplo (m.c.m.), poiché tutti i numeri condividono un MCD o un m.c.m. se il primo numero è un intero.

Ciò significa che l'MCD (vedi calcolatore MCD) è semplicemente il numero più piccolo della sequenza. Al contrario, l'm.c.m. è semplicemente il numero più grande della sequenza. Ad esempio, nella sequenza 3, 6, 12, 24, 48 l'MCD è 3 e l'm.c.m. sarebbe 48. Ma se consideriamo solo i numeri 6, 12, 24 l'MCD sarebbe 6 e l'm.c.m. sarebbe 24.

Progressione geometrica — Che cos'è la progressione geometrica?

Vediamo ora cos'è una progressione geometrica in termini di "persone". Una progressione geometrica è un insieme di numeri specifici che sono legati dal rapporto comune di cui abbiamo parlato prima. Questo rapporto comune è una delle caratteristiche che definiscono una determinata sequenza, insieme al termine iniziale di una sequenza. Vedremo più avanti come questi due numeri sono alla base della definizione di progressione geometrica e, a seconda di come vengono utilizzati, si può ottenere la formula esplicita di una progressione geometrica o la formula inversa equivalente per la progressione geometrica.

Esempi di progressioni geometriche con rapporti di 1/2, 1/3, 1/4 e con il termine iniziale di 1. — Esempi di progressione geometrica con rapporti diversi.

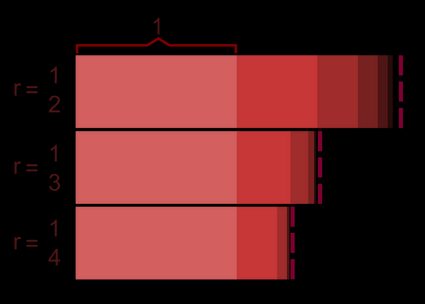
Ora, costruiamo una semplice progressione geometrica utilizzando valori concreti per questi due parametri di definizione. Per semplificare le cose, il termine iniziale sarà $1$ e il rapporto sarà impostato su $2$ . In questo caso, il primo termine sarà $a_1 = 1$ per definizione, il secondo termine sarà $a_2 = a_1 × 2 = 2$ , il terzo termine sarà $a_3 = a_2 × 2 = a_1 × 2^2 = 4$ , etc. Il termine n-esimo della progressione sarà quindi:

a_{n} = 1 \times 2^{{n}-1}

dove $n$ è la posizione del termine in questione nella progressione.

Come puoi vedere, il rapporto tra due termini consecutivi della progressione — definito proprio come nel nostro calcolatore del rapporto 🇺🇸 — è costante e uguale al rapporto comune.

Un modo comune di scrivere una progressione geometrica è quello di scrivere esplicitamente i primi termini. In questo modo è possibile calcolare qualsiasi altro numero della progressione; per il nostro esempio, scriveremmo la serie come:

1, 2, 4, 8, ...

Tuttavia, esistono altri modi matematici per fornire le stesse informazioni. Questi altri modi sono la cosiddetta formula esplicita e inversa delle progressioni geometriche. Ora che abbiamo capito cos'è una progressione geometrica, possiamo approfondire questa formula ed esplorare modi per trasmettere le stesse informazioni con meno parole e con maggiore precisione.

Formula inversa e formula esplicita per la progressione geometrica

Esistono due modi distinti in cui è possibile rappresentare matematicamente una progressione geometrica con una sola formula — la formula esplicita per una progressione geometrica e la formula inversa per una progressione geometrica. La prima è quella che abbiamo già visto nel nostro esempio di serie geometrica. Abbiamo visto la formula esplicita specifica per quell'esempio, ma puoi scrivere una formula valida per qualsiasi progressione geometrica — puoi sostituire i valori di $a_1$ con il termine iniziale corrispondente e di $r$ con il rapporto. La formula generale per il termine n-esimo è:

a_{n} = a_{1}r^{{n}-1}, n \in \mathbb N

dove $n \in \mathbb N$ significa che $n = 1, 2, 3, ...$ . La formula inversa per le progressiomi geometriche trasmette le informazioni più importanti su una progressione geometrica — il termine iniziale $a_1$ , il modo in cui ottenere qualsiasi termine dal primo e il fatto che non esiste un termine prima di quello iniziale.

Esiste un altro modo per mostrare le stesse informazioni utilizzando un altro tipo di formula — la formula ricorsiva di una progressione geometrica. È composta da due parti che indicano informazioni diverse dalla definizione di progressione geometrica. La prima parte spiega come passare da un membro qualsiasi della progressione a un altro membro utilizzando il rapporto. Questo significato da solo non è sufficiente per costruire una progressione geometrica da zero, poiché non conosciamo il punto di partenza. Questa è la seconda parte della formula, il termine iniziale (o qualsiasi altro termine). Vediamo come si presenta questa formula ricorsiva:

\begin{align*} a_{n} &= a_{n-1} r \\ a_{i} &= x \end{align*}

dove $x$ viene utilizzato per esprimere il fatto che qualsiasi numero verrà utilizzato al suo posto, ma anche che deve essere un numero esplicito e non una formula. Il pedice $i$ indica qualsiasi numero naturale (proprio come $n$ ), ma viene utilizzato al posto di $n$ per chiarire che $i$ non deve essere necessariamente lo stesso numero di $n$ .

Come si usa il calcolatore della progressione geometrica?

Ora che sai cos'è una progressione geometrica e come scriverne una sia in formula inversa che esplicita, è arrivato il momento di applicare le tue conoscenze e calcolare qualcosa! Con il nostro strumento puoi calcolare tutte le proprietà delle progressioni geometriche, come il rapporto comune, il termine iniziale, l'ultimo termine n-esimo, etc. Ecco una breve descrizione di come è strutturato il calcolatore:

Per prima cosa, dicci cosa sai della tua progressione scegliendo il valore del Tipo:
- Il rapporto comune e il primo termine della progressione;
- Il rapporto comune e un n^esimo termine; oppure
- Due termini;
Inserisci i tuoi dati. In base a questi dati, il calcolatore determina l'intero della progressione geometrica; e
Per impostazione predefinita, il calcolatore visualizza i primi cinque termini della progressione. Puoi cambiare i termini iniziali e finali in base alle tue esigenze.

Il nostro strumento può anche calcolare la somma della tua sequenza — tutta o una parte finale. In quest'ultimo caso, è sufficiente inserire il punto iniziale e finale della somma e potrai goderti il risultato. Come imparerai nelle sezioni successive, la somma infinita potrebbe non esistere

Formula della serie geometrica — la somma di progressioni geometriche

Finora abbiamo parlato di progressioni geometriche o sequenze geometriche, che sono collezioni di numeri. Tuttavia, ci sono risultati davvero interessanti da ottenere quando si provano a sommare i termini di una progressione geometrica. Quando abbiamo una progressione geometrica finita, che ha un numero limitato di termini, il processo è semplice come trovare la somma di una progressione di numeri lineari. Il calcolo per la somma di questa progressione geometrica può anche essere fatto a mano, teoricamente.

Ma possiamo essere più efficienti utilizzando la formula della serie geometrica e giocando con essa. Per farlo, utilizzeremo il segno matematico della somma $\Sigma$ , che significa sommare ogni termine successivo. Ad esempio, se abbiamo una progressione geometrica denominata a_n e nominiamo la somma della progressione geometrica S, la relazione tra le due sarà:

\scriptsize S = \sum_{n=1}^m a_{n} = a_{1} + a_{2} + a_{3} + ... + a_m

se vogliamo sommare i primi m termini, oppure:

\scriptsize S = \sum_{n=1}^\infty a_{n} = a_{1} + a_{2} + a_{3} + \ldots

se vogliamo sommare tutti i termini.

Purtroppo, questo ti lascia ancora con il problema di calcolare effettivamente il valore della serie geometrica. Puoi sempre usare questo calcolatore come calcolatore della progressione geometrica, ma sarebbe molto meglio se, prima di usare un qualsiasi calcolatore per le somme geometriche, tu comprendessi come farlo manualmente. Esiste un trucco che può rendere il nostro lavoro molto più semplice e consiste nel modificare e risolvere l'equazione della progressione geometrica in questo modo:

\scriptsize \begin{align*} S &= \sum_{n=1}^m a_{n} = \\ &= a_{1} + a_{1}r + a_{1}r^2 + ... + a_{1}r^{m-1} \end{align*}

Ora moltiplica entrambi i lati per $(1-r)$ e risolvi:

\scriptsize \begin{align*} \scriptsize S (1 - r) &= (1 - r) (a_1 + a_1r + a_1r^2 + \ldots +\ a_1r^{m-1}) \\[1.5em] S(1-r) &= a_1 + a_1r + ... + a_1r^{m-1} \\ &\ -(a_1r + a_1r^2 + \ldots + a_1r^{m}) \\[.5em] &= a_1 - a_1r^{m} \end{align*}

\scriptsize S = \sum_{n=1}^m a_{n} = a_1 - a_1 \frac{r^{m}}{1-r} = a_1 \frac{1-r^m}{1-r}

Questo risultato è facilmente calcolabile da solo e rappresenta la formula di base della serie geometrica quando il numero di termini della serie è finito. Tuttavia, questa è la matematica e non la Vita Reale™, quindi possiamo avere un numero infinito di termini nella nostra serie geometrica ed essere comunque in grado di calcolare la somma totale di tutti i termini. Come funziona questa magia? — Ti sento chiedere. Beh, non temere, ti spiegheremo tutti i dettagli, giovane apprendista.

Utilizzare la formula della progressione geometrica per calcolare la somma infinita

Dopo aver visto come ottenere la formula della serie geometrica per un numero finito di termini, è naturale (almeno per i matematici) chiedersi come posso calcolare la somma infinita di una progressione geometrica? Potrebbe sembrare impossibile, ma alcuni trucchi ci permettono di calcolare questo valore in pochi semplici passi. Per questo, dobbiamo introdurre il concetto di limite. Si tratta di un processo matematico grazie al quale possiamo capire cosa succede all'infinito. Può anche essere utilizzato per cercare di definire matematicamente espressioni che di solito non sono definite, come ad esempio zero diviso per zero o zero alla potenza di zero.

Parlare di limiti è un argomento molto complesso, che vade al di là dello scopo di questo calcolatore. La loro complessità è il motivo per cui abbiamo deciso di menzionarli e di non entrare nel dettaglio di come calcolarli. Non preoccuparti però, perché puoi trovare ottime informazioni nell'articolo di Wikipedia sui limiti.

Anche se non puoi preoccuparti di controllare quali sono i limiti, puoi comunque calcolare la somma infinita di una serie geometrica utilizzando il nostro calcolatore. L'unica cosa che devi sapere è che non tutte le serie hanno una somma definita. Le condizioni che una serie deve soddisfare affinché la sua somma sia un numero (questo è ciò che i matematici chiamano convergenza) sono, in linea di principio, semplici. Le spieghiamo nella sezione seguente.

Osservazioni sull'utilizzo del calcolatore come calcolatore della progressione geometrica

Quando si parla di serie matematiche (sia progressione geometriche che aritmetiche), queste vengono spesso raggruppate in due diverse categorie, a seconda che la loro somma infinita sia finita (serie convergente) o infinita/non definita (serie divergente). Il modo migliore per sapere se una serie è convergente o meno è calcolare la sua somma infinita utilizzando i limiti. A parte questo, ci sono alcuni trucchi che ci permettono di distinguere rapidamente tra serie convergenti e divergenti senza dover fare tutti i calcoli. Questi trucchi includono — guardare il termine iniziale e quello generale, guardare il rapporto o fare un confronto con altre serie.

Visualizzazione della somma di una sequenza geometrica con un termine iniziale di 1 e un rapporto di 1/2 sotto forma di area di un rettangolo divisa in rettangoli sempre più piccoli. — Visualizzazione della somma di una progressione geometrica.

Affinché una serie sia convergente, il termine generale $a_n$ deve diventare più piccolo per ogni aumento del valore di $n$ . Se $a_n$ diventa più piccolo, non possiamo garantire che la serie sia convergente, ma se $a_n$ è costante o diventa più grande all'aumentare di $n$ , possiamo dire con certezza che la serie sarà divergente. Se non siamo sicuri che $a_n$ diventi più piccolo, possiamo osservare il termine iniziale e il rapporto, oppure calcolare alcuni dei primi termini. Questo ci darà un'idea di come si evolve $a_n$ .

La seconda opzione è quella di confrontare l'evoluzione della nostra progressione geometrica con una che sappiamo con certezza convergere (o divergere), cosa che si può fare con una rapida ricerca online. In linea generale, se la serie che stiamo analizzando è più piccola (cioè $a_n$ è più piccola) di una serie che sappiamo per certo che converge, possiamo essere certi che anche la nostra serie convergerà. Al contrario, se la nostra serie è più grande di una che sappiamo per certo essere divergente, la nostra serie divergerà sempre. Negli altri casi (più grande di una convergenza o più piccola di una divergenza) non possiamo dire nulla sulla nostra serie geometrica e siamo costretti a trovare un'altra serie con cui confrontarla o a utilizzare un altro metodo.

Questi criteri si applicano alle progressioni aritmetiche e geometriche. Infatti, queste due sono molto correlate tra loro ed entrambe le progressioni possono essere collegate dalle operazioni di esponenziazione e di calcolo dei logaritmi.

Il paradosso di Zenone e altri esempi di progressioni geometriche

Abbiamo già visto un esempio di progressione geometrica sotto forma della cosiddetta progressione delle potenze di due. Si tratta di una progressione molto importante a causa dei computer e della loro rappresentazione binaria dei dati. In questa progressione possiamo trovare valori come il numero massimo consentito in un computer (varia a seconda del tipo di variabile utilizzata), il numero di byte in un gigabyte o il numero di secondi che mancano alla fine dell'ora UNIX (sia valori originali che patched).

Oltre alla progressione di potenze di due, possiamo avere qualsiasi altra progressione di potenze se sostituiamo semplicemente $r = 2$ con il valore della base che ci interessa. Le serie di potenze sono comunemente utilizzate e conosciute e possono essere espresse con la comoda formula della progressione geometrica. Ma queste progressioni di potenze di qualsiasi tipo non sono le uniche progressioni che possiamo avere, e ti mostreremo progressioni geometriche ancora più importanti o interessanti come la serie alternata o il sorprendente paradosso di Zenone.

Iniziamo con i paradossi di Zenone, in particolare il cosiddetto paradosso della dicotomia. Questo paradosso è in fondo solo un rompicapo matematico sotto forma di serie geometrica infinita. Zenone era un filosofo greco precedente a Socrate. Egli ideò un meccanismo per dimostrare che il movimento era impossibile e che non sarebbe mai dovuto accadere nella vita reale. L'idea è quella di dividere a metà la distanza tra il punto di partenza (A) e il punto di arrivo (B). Una volta che hai coperto la prima metà, dividi di nuovo a metà la distanza rimanente... Puoi ripetere questo processo tutte le volte che vuoi, il che significa che ti rimarrà sempre una certa distanza da percorrere per arrivare al punto B.

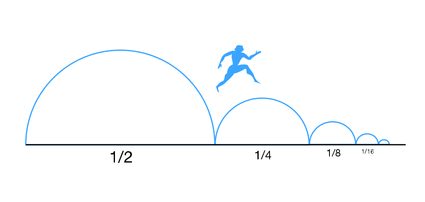
Visualizzazione del paradosso di Zenone (dicotomia). Il velocista greco corre ogni volta 1/2 della lunghezza della distanza precedente, senza mai completare la corsa. — Visualizzazione del paradosso di Zenone (dicotomia).

Il paradosso di Zenone sembra prevedere che, poiché abbiamo un numero infinito di metà da percorrere, avremmo bisogno di una quantità infinita di tempo per viaggiare da A a B. Tuttavia, come sappiamo dalla nostra esperienza quotidiana, questo non è vero e possiamo sempre arrivare dal punto A al punto B in un tempo finito (ad eccezione degli spagnoli che sembrano sempre arrivare infinitamente in ritardo ovunque). La soluzione a questo apparente paradosso può essere trovata utilizzando la matematica.

Se esprimiamo il tempo necessario per andare da A a B (chiamiamolo $t$ per ora) sotto forma di serie geometrica, avremo una serie definita da — $a_1 = t/2$ con il rapporto comune $r = 1/2$ . Quindi, per percorrere la prima metà del tragitto $t/2$ impiegheremo la metà della distanza rimanente in $t/4$ , poi $t/8$ , etc. Se ora eseguiamo la somma infinita delle serie geometriche, troveremo che:

\scriptsize\begin{align*} S &= \sum_{n=1}^\infty a_n = \frac{t}{2} + \frac{t}{4} + ... \\[1em] &= t × \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...\right) = t × 1 = t \end{align*}

Questa è la prova matematica che possiamo andare da A a B in un tempo finito ( $t$ in questo caso).

Per finire, e nel caso in cui il paradosso di Zenone non fosse abbastanza sconvolgente, parliamo della serie di unità alternate.

Questa serie inizia con $a_1 = 1$ e ha un rapporto $r = -1$ che produce una serie della forma:

\scriptsize S = \sum_{n=1}^\infty a_n = 1 - 1 + 1 - 1 + ...

Questo non converge secondo i criteri standard perché il risultato dipende dal numero di termini pari ( $S = 0$ ) o dispari ( $S = 1$ ). Esiste però un trucco per "far convergere" questa serie a un numero finito. Il trucco in sé è molto semplice, ma si basa su argomentazioni matematiche (e persino metamatematiche) molto complesse, quindi se lo mostrerai a un matematico rischierai di finire in grossi guai (otterresti una reazione simile parlando della famigerata congettura di Collatz). Sei stato avvisato. Vediamo la "soluzione":

\scriptsize S = 1 - 1 + 1 - 1 + ...

Moltiplichiamo entrambi i lati per $-1$ :

\scriptsize\begin{align*} -S &= -1 + 1 - 1 + 1 - ... \\[1em] &= -1 + (1 - 1 + 1 - 1 + ...) \\[1em] &= -1 + S \end{align*}

Se ora risolviamo per $S$ :

\scriptsize -S - S = -1 → 2S = 1 → S = 1/2

Ora puoi andare a mostrarlo ai tuoi amici, a patto che non siano matematici.

FAQ

Che cos'è la progressione geometrica?

Una progressione geometrica è una serie di numeri in cui il termine successivo si ottiene moltiplicando il termine precedente per un numero comune.

Come si trova la somma di una progressione geometrica?

Per trovare la somma di una progressione geometrica:

Calcola il rapporto comune, r elevato alla potenza n;
Sottrai il risultato rⁿ da 1;
Dividi il risultato per (1 - r); e
Moltiplica il risultato per il primo termine, a₁.

Come trovare l'n-esimo termine di una progressione geometrica?

Trovare l'n-esimo termine di una progressione geometrica:

Calcola il rapporto comune elevato alla potenza (n - 1); e
Moltiplica la risultante per il primo termine, a.

Come si calcola il rapporto comune di una progressione geometrica?

Per calcolare il rapporto comune di una progressione geometrica, dividi due termini consecutivi qualsiasi della progressione.

Álvaro Díez and Anna Szczepanek, PhD

Formula to find the n-th term of the geometric sequence:

Type

Common ratio r

a₁

Here's your sequence

Starting from term no.

Up to term no.

a₁ =

a₂ =

a₃ =

a₄ =

a₅ =

Summing the sequence

Find

a₁ + a₂ + a₃ + ... =

To increase the precision of calculations, go to the advanced mode.

Arithmetic sequenceCollatz conjectureConvolution… 7 more