Calcolatore per l'Area del Prisma Rettangolare

Eccoti sul calcolatore per l'area del prisma rettangolare, dove avrai la possibilità di imparare tutto sul tuo prisma in modo semplice e veloce. In particolare, ti spiegheremo come trovare la superficie di un prisma rettangolare. Vuoi dipingere un fienile e ti stai chiedendo quanta vernice mi serve 🇺🇸? Oppure stai costruendo una piscina nel tuo giardino e vuoi sapere quante piastrelle ti servono?

Non importa quale sia la domanda, purché si riduca a "quale è l'area della superficie di un prisma rettangolare", sei nel posto giusto!

Prima di vedere qual è la superficie di un prisma rettangolare, dobbiamo familiarizzare con il prisma stesso.

Immagina una scatola. Una normale scatola rettangolare, come quelle che vedi al supermercato, piena di qualsiasi prodotto. Ecco, quello è un prisma rettangolare! Oppure ti ricordi i disegni delle case che facevamo all'asilo? Rimuovi il tetto angolare e ti ritroverai con un altro esempio di prisma rettangolare.

Dal punto di vista formale (matematico), un prisma rettangolare retto è un solido in cui tutti e sei i lati sono rettangoli perpendicolari tra loro. In particolare, questo significa che ci sono tre coppie di facce identiche posizionate sui lati opposti del solido.

Inoltre, come per qualsiasi altra definizione scientifica, ci sono alcuni nomi particolari associati al prisma. Le facce inferiore e superiore della scatola sono chiamate basi, mentre ciascuna delle altre quattro è chiamata faccia laterale. Infine, i lati di ogni rettangolo sono chiamati spigoli (sempre divisi in spigoli di base e spigoli laterali).

È ora di mettere da parte le parole altisonanti e concentrarci su come trovare la superficie di un prisma rettangolare.

Per capire qual è la superficie di un prisma rettangolare, dobbiamo conoscere tutti e tre i suoi lati. Cominciamo con la notazione che utilizziamo per questi e per gli altri valori del nostro calcolatore per l'area superficiale di un prisma rettangolare:

• l — Lunghezza del primo spigolo di base;
• w — Lunghezza del secondo spigolo di base;
• h — Lunghezza del bordo laterale (chiamata anche altezza del prisma);
• Area della base — Area di base del prisma;
• Area laterale — Area laterale del prisma;
• A — Area della superficie del prisma; e
• V — Volume del prisma.

Nota che Area della base indica l'area della superficie di una singola base del prisma. D'altra parte, Area laterale indica l'area laterale, cioè l'area totale delle quattro facce laterali. Pertanto, dato che il solido ha due basi (quella inferiore e quella superiore), la formula dell'area superficiale di un prisma rettangolare è la seguente:

Area = 2 × area della base + area laterale,

che, nella nostra notazione, si traduce in

Area = 2 × A_b + A_l.

Ricordiamo che tutte le facce del nostro calcolatore sono rettangoli e, come indicato nel calcolatore per l'area del rettangolo, si calcolano moltiplicando le lunghezze dei lati. Ora utilizziamo queste informazioni per studiare la base del nostro prisma. Con la nostra notazione, si tratta di un rettangolo con lati l e w, quindi la sua area è l × w. E questa è proprio la formula dell'area della base:

Area della base = l × w.

Un gioco da ragazzi, vero? Bene, proviamo ora a fare qualcosa di un po' più complicato e passiamo all'area laterale. Abbiamo quattro facce che contribuiscono a questo valore e tutte sono rettangoli. Inoltre, tra le quattro, ci sono due coppie di facce identiche (la parete anteriore e posteriore e la parete sinistra e destra). Tutti questi hanno un lato uguale a h, il bordo laterale (o l'altezza) del prisma. Inoltre, l'altro lato di una delle coppie è uguale al primo spigolo di base, ossia l, e l'altro è uguale alla lunghezza del secondo, ossia w. In definitiva, otteniamo che l'area laterale, o Area laterale come la chiamiamo noi, è

Area laterale = l × h + l × h + w × h + w × h,

o semplicemente

Area laterale = 2 × l × h + 2 × w × h.

Osserva che, insieme all'area di base, questo ci permette di tradurre la formula della superficie di un prisma rettangolare in

Area = 2 × area della base + area laterale = 2 × l × w + 2 × l × h + 2 × w × h.

Supponiamo che stia cercando di piastrellare una piscina e che voglia conoscere l'area da piastrellare. Se la piscina è rettangolare con il fondo piatto, allora abbiamo a che fare proprio con un prisma rettangolare! Vediamo una bella immagine per capirlo chiaramente.

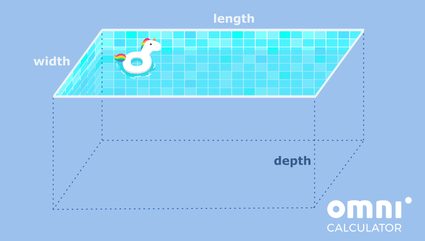
Ok, sappiamo che è difficile distogliere lo sguardo dall'unicorno gonfiabile, ma torniamo al problema in questione!

Diciamo che la piscina ha una lunghezza di 2 metri, una larghezza di 3 metri e una profondità di 3 metri. Ora che abbiamo i numeri, proviamo a metterli in termini con la notazione che abbiamo usato sopra.

Innanzitutto, i lati della base della nostra piscina sono la sua lunghezza e la sua larghezza, che nel nostro caso sono rispettivamente 8 metri e 6 metri. Dato che stiamo usando l e w come bordi della base, possiamo usare questi numeri nel calcolatore per impostare l = 8 m e w = 6 m. Nota che non importa in quale ordine li mettiamo; questo si traduce solo nel guardare la piscina da un'altra angolazione e non cambia la sua superficie.

Ci rimane la profondità della piscina e il numero h nel calcolatore. Ed è esattamente quello che dobbiamo fare ora: impostare h = 5 m, che è la profondità della piscina o l'altezza del prisma.

"E abbiamo finito, non è vero?" Non esattamente... Il calcolatore per l'area del prisma rettangolare ci dà la risposta:

Area = 2 × l × w + 2 × l × h + 2 × w × h = 2 × 8 m × 6 m + 2 × 8 m × 5 m + 2 × 6 m × 5 m = 236 m².

Ma questa è la superficie dell'intero prisma e non vogliamo piastrellare 🇺🇸 tutto intorno. Dopotutto, se piastrellassimo la parte superiore, sarebbe piuttosto difficile entrare (o uscire), no? Si tratterebbe di una cattiveria di alto livello, persino peggiore della rimozione della scala per i tuoi Sims.

Per trovare la risposta corretta, passiamo alla modalità avanzata. Questa ci permette di vedere l'area di base e l'area laterale del solido. Dal momento che sappiamo come trovare l'area superficiale di un prisma rettangolare, cioè sappiamo che

Area = 2 × area della base + area laterale,

dobbiamo solo sottrarre da questa l'area extra che non stiamo piastrellando. E questo è la parte superiore. Ma la base superiore è la stessa di quella inferiore, quindi l'area che dobbiamo piastrellare è, di fatto:

Area da piastrellare = area - area della base,

che, nel nostro caso, è:

Superficie inclinata = 236 m² - 48 m² = 188 m².

Questo ci porta a un passo dal finire la piscina e a poter ammirare il tuo lavoro bevendo una birra fresca. Detto questo, il prisma non è l'unica forma 3D a base rettangolare; scopri di più sul calcolatore per l'area di una piramide rettangolare 🇺🇸.