Calculateur d'aire d’un secteur

Avec ce calculateur d'aire d’un secteur, vous trouverez rapidement l'aire d’un secteur de n'importe quel cercle, par exemple l'aire d'un demi-cercle ou d'un quadrant. Dans ce court article, nous allons :

• fournir une définition du secteur et expliquer ce qu'est le secteur d'un cercle ;
• montrer la formule de l'aire d'un secteur et expliquer comment dériver l'équation soi-même sans trop d'efforts ;
• donner quelques exemples de la vie de tous les jours pour lesquels le calculateur d'aire d’un secteur peut s'avérer utile.

Commençons par la définition d'un secteur – qu'est-ce qu'un secteur en géométrie ?

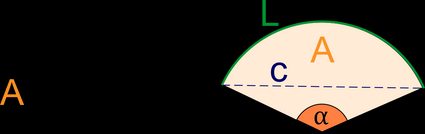
Un secteur est une figure géométrique délimitée par deux rayons et un arc de cercle, qui est compris entre ces deux rayons.

Les secteurs d'un cercle sont le plus souvent représentés dans des diagrammes circulaires, où un cercle est divisé en plusieurs secteurs pour montrer la pondération de chaque segment. Les images ci-dessous montrent quelques exemples de secteurs de cercle – cela ne signifie pas nécessairement qu'ils ressembleront à une part de tarte, mais parfois, ils ressemblent au reste de la tarte après en avoir pris une part :

Il est très rare que vous entendiez parler du secteur d'une ellipse, mais sachez que les formules sont beaucoup, beaucoup plus difficiles à utiliser que les équations de l'aire du secteur d'un cercle.

La formule pour calculer l'aire d'un secteur est simple : il suffit de multiplier l'angle au centre par le rayon au carré, puis de diviser par 2 :

• Aire du secteur = r² × α / 2

Mais d'où vient-elle ? Vous pouvez la trouver en utilisant les proportions. Tout ce dont vous avez besoin, c'est de vous souvenir de la formule de l'aire du cercle (et nous sommes sûrs que c'est le cas !).

1. L'aire d'un cercle se calcule comme suit : A = πr². C'est déjà un bon point de départ.

2. L'angle complet est de 2π en radians, ou de 360° en degrés, cette dernière unité étant la plus courante.

3. Ensuite, nous voulons calculer l'aire d'une partie d'un cercle, exprimée par l'angle au centre :

   • pour des angles de 2π (cercle complet), l'aire est égale à πr² :

     2π → πr²

   • alors, quelle est l'aire du secteur d'un cercle ?

     α → Aire du secteur

4. À partir de la proportion, nous pouvons facilement trouver la formule finale de l'aire du secteur.

   Aire du secteur = α × πr² / 2π = α × r² / 2

La même méthode peut être utilisée pour trouver la longueur d'un arc de cercle : il suffit de se souvenir de la formule de la circonférence d'un cercle. Pour en savoir plus, consultez nos calculateur de circonférence et calculateur de longueur d'arc de cercle.

Trouver l'aire d'un demi-cercle ou d'un quadrant devrait être un jeu d'enfant maintenant. Il suffit de penser à la partie de cercle qu'ils représentent !

1. Aire du demi-cercle : πr² / 2

• Sachant qu'il s'agit de la moitié du cercle, on divise l'aire par 2 :

  Aire du demi-cercle = Aire du cercle / 2 = πr² / 2

• Bien entendu, vous obtiendrez le même résultat en utilisant la formule de l'aire du secteur. Rappelez-vous simplement que l'angle droit est π (180°) :

  Aire du demi-cercle = α × r² / 2 = πr² / 2

2. Aire du quadrant : πr² / 4

• Comme un quadrant est un quart de cercle, nous pouvons écrire la formule comme suit :

  Aire du quadrant = Aire du cercle / 4 = πr² / 4

• L'angle au centre du quadrant est un angle droit (π/2 ou 90°), ce qui permet d'obtenir rapidement la même équation :

  Aire du quadrant = α × r² / 2 = πr² / 4

On sait ce que vous allez dire : pourquoi devons-nous apprendre cela ? On ne va jamais s'en servir. Eh bien, nous aimerions vous montrer que la géométrie est partout autour de nous !

• Si vous vous demandez quelle taille de gâteau, vous devez commander pour votre super fête d'anniversaire – bingo, vous êtes au bon endroit ! Utilisez la formule de l'aire du secteur pour estimer la taille d'une part 🍰 pour vos invités afin que personne ne meure de faim.

• Il en va de même pour les pizzas – avez-vous remarqué que chaque part est un secteur d'un cercle 🍕 ? Par exemple, si vous n'êtes pas un grand fan de la croûte, vous pouvez calculer quelle taille de pizza vous permettra de faire la meilleure affaire.

• Y a-t-il des passionnés de couture ici ?👗 Le calcul de l'aire d'un secteur peut s'avérer utile pour préparer une jupe circulaire (car il ne s'agit pas toujours d'un cercle complet, mais plutôt du secteur d'un cercle).

En dehors de ces exemples simples et concrets, la formule de l'aire d’un secteur peut être utile en géométrie, par exemple pour trouver la superficie d'un cône 🇺🇸.