Calculateur de diagonale d'un rectangle

Notre calculateur de diagonale d'un rectangle est un outil complet qui permet de trouver rapidement la diagonale et les autres paramètres d'un rectangle. Avez-vous un problème de géométrie à résoudre et vous ne savez pas comment trouver la diagonale d'un rectangle ? Entrez quelques paramètres dans les champs à côté du texte ou continuez à lire pour découvrir toutes les formules de la diagonale d'un rectangle.

La figure ci-dessous vous montre un rectangle classique. Nous avons marqué cinq paramètres de base que vous pouvez utiliser pour dériver la formule de la diagonale d'un rectangle. Ce sont :

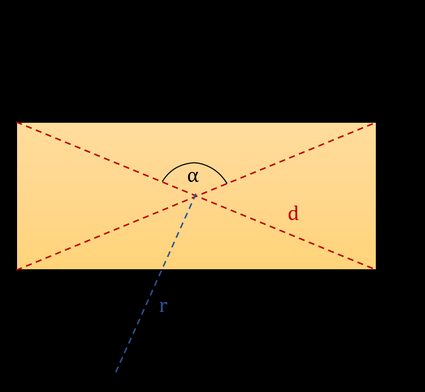
• l – longueur
• w – largeur
• α – l'angle entre les diagonales
• r – rayon du cercle circonscrit
• d – diagonale 

et deux autres paramètres qui ne sont pas indiqués sur l'image :

• A – aire 
• P – périmètre

Le terme « rectangle » vient du latin rectangulus, qui est une combinaison de deux mots : rectus (droit, propre) et angulus (angle). Ce nom vient du fait qu'un rectangle est un quadrilatère à quatre angles droits (4 × 90° = 360°). Ses côtés opposés sont parallèles et de la même longueur, et ses deux diagonales se coupent en leur milieu et sont également de même longueur.

Un carré est un cas particulier de rectangle : ses quatre côtés ont la même longueur. À différence d'un rectangle, l'angle entre les deux diagonales d'un carré est droit. Découvrez nos calculateurs dédiés aux carrés, par exemple le calculateur de carré 🇺🇸. Ils peuvent rapidement estimer le périmètre, l'aire et la diagonale d'un carré donné, à partir de la seule longueur d'un côté.

Le centre d'un rectangle est équidistant de ses sommets ; vous pouvez donc toujours tracer son cercle circonscrit. En revanche, il est impossible d'inscrire un cercle dans un rectangle n'étant pas un carré.

Pour déterminer la diagonale d'un rectangle :

1. Déterminez les côtés du rectangle, que l'on désigne par w et l.
2. Élevez ces deux valeurs au carré, c'est-à-dire calculez l² et w².
3. Additionnez les deux valeurs obtenues à l'étape 2.
4. Prenez la racine carrée du résultat.
5. C'est tout ! Vous avez trouvé la longueur de la diagonale de votre rectangle.

Pourquoi cette formule fonctionne-t-elle ?

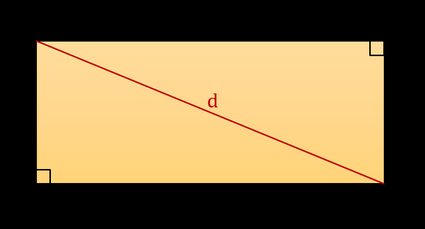
Pour dériver la formule de la diagonale d'un rectangle utilisée ci-dessus, il faut diviser un rectangle en deux triangles rectangles congruents, c'est-à-dire des triangles dont l'un des angles est égal à 90°. Chaque triangle aura des côtés de longueur l et w et une hypoténuse de longueur d. Vous pouvez alors utiliser la formule de l'hypoténuse, par exemple à partir du théorème de Pythagore, pour trouver la longueur de la diagonale d'un rectangle, qui peut être exprimée avec la formule suivante :

d² = l² + w²

Et maintenant, vous devriez être capable de trouver la formule explicite pour calculer la diagonale d'un rectangle – il suffit de prendre une racine carrée des deux membres de l'équation :

d = √(l² + w²)

Notre calculateur de diagonale d'un rectangle vous permet d'utiliser presque toutes les unités désirées. Consultez notre convertisseur de longueur ou notre calculateur d'aire 🇺🇸 pour savoir comment passer d'une unité à l'autre (SI et impériale).

Parfois, on ne connait pas la longueur des deux côtés adjacents d'un rectangle. Comment trouver la diagonale d'un rectangle dans cette situation ? La réponse est fournie par notre calculateur de diagonale d'un rectangle. Tout d'abord, il faut noter trois équations de base pour l'aire, le périmètre et le rayon du cercle circonscrit :

1. l'aire – A = w × l ;
2. le périmètre – P = 2 × w + 2 × l ; et
3. le rayon du cercle circonscrit – r = d/2.

Avec les équations ci-dessus, il est maintenant possible de dériver diverses formules de diagonale d'un rectangle qui sont utilisées par ce calculateur de diagonale d'un rectangle :

1. Étant donné la longueur et la largeur :
   d = √(l² + w²)

2. Étant donné l'aire et, soit la longueur, soit la largeur :
   d = √(A²/l² + l²) ou d = √(A²/w² + w²)

3. Étant donné le perimètre et, soit la longueur, soit la largeur :
   d = √(2l² - P × l + P²/4)) ou d = √(2w² - P × w + P²/4)

4. Étant donné l'angle et, soit la longueur, soit la largeur :
   d = w / sin(α/2) ou d = l / cos(α/2)

5. Étant donné l'aire et le périmètre :
   d = ½√(P² - 8 × A)

6. Étant donné l'aire et l'angle :
   d = √(2 × A / sin(α))

7. Étant donné le périmètre et l'angle :
   d = P / (2 × sin(α/2) + 2 × cos(α/2))

8. Étant donné le rayon du cercle :
   d = 2 × r

Remarque : L'angle α est celui entre les diagonales, du côté de la longueur l, comme sur la première image. N'oubliez pas non plus que le calculateur de diagonale d'un rectangle part du principe que la longueur est plus grande que la largeur !

Savez-vous qu'il existe un rectangle spécial appelé rectangle d'or ? Si ce n'est pas le cas, consultez notre calculateur de rectangle d'or 🇺🇸 pour apprendre comment tracer des rectangles d'or !