Calculateur d'angle entre deux vecteurs

Avec ce calculateur d'angle entre deux vecteurs, vous apprendrez rapidement à trouver l'angle entre deux vecteurs. Peu importe que vos vecteurs soient à 2 ou 3 dimensions, ou qu'ils soient représentés par leurs coordonnées, origines ou extrémités – notre outil est une valeur sûre dans tous les cas. Amusez-vous avec notre calculateur et n'hésitez pas à poursuivre votre lecture pour en apprendre plus sur les vecteurs en général. Si vous cherchez la définition des vecteurs ou les formules pour calculer l'angle entre deux vecteurs, vous les trouverez certainement ici.

Dans ce paragraphe, vous trouverez les formules pour calculer l'angle entre deux vecteurs – oui oui, uniquement les formules. Si vous souhaitez comprendre comment nous les dérivons, passez directement au paragraphe suivant : Comment trouver l'angle entre deux vecteurs ?

Angle entre deux vecteurs à 2 dimensions

1. Vecteurs représentés par des coordonnées (notation standard) :

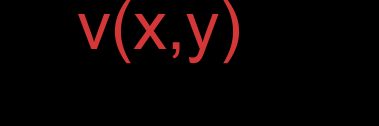
Pour le vecteur $\boldsymbol a$ :

Et $\boldsymbol b$ :

L'angle est le suivant :

2. Vecteurs définis par leur origine et leur extrémité :

Pour le vecteur $\boldsymbol a$ :

Et :

Le vecteur $\boldsymbol a$ est donc :

Pour le vecteur $\boldsymbol b$ :

Et :

Le vecteur $\boldsymbol b$ est donc :

Donc :

Angle entre deux vecteurs à 3 dimensions

1. Vecteurs représentés par des coordonnées :

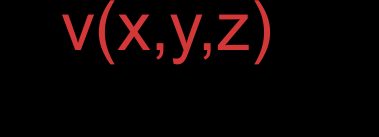
Et :

Donc :

2. Vecteurs définis par leur origine et leur extrémité :

Pour le vecteur $\boldsymbol{a}$ :

Et :

Donc :

Pour le vecteur $\boldsymbol{b}$ :

Et :

Donc :

Trouvez la formule finale de manière analogue à la version 2D :

Il est également possible d'avoir un vecteur défini par des coordonnées et l'autre par une origine et une extrémité, mais nous n'allons pas compliquer davantage cette section. L'essentiel est que notre calculateur d'angle entre deux vecteurs vous propose toutes les combinaisons possibles.

OK, le paragraphe précédent était un peu long. Pour mieux comprendre les formules d'un angle entre deux vecteurs, voyons comment on en est arrivé là :

1. Commençons par le début : la formule géométrique de base pour calculer le produit scalaire 🇺🇸 :

   Le produit scalaire est défini comme le produit des normes des vecteurs par le cosinus de l'angle qui les sépare (noté ici $\alpha$) :

2. Ensuite, mettez l'angle au premier plan de l'équation :

   Divisez le produit scalaire par le produit des normes des vecteurs :

Prenez l'inverse du cosinus des deux côtés :

3. Aussi, nous devons nous rappeler la définition de la norme d'un vecteur :

   La norme d'un vecteur, également appelée magnitude ou longueur d'un vecteur, est la racine carrée de la somme des composantes du vecteur au carré. Nous avons donc :

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ sur le plan 2D ; et

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ sur le plan 3D.

Avez-vous remarqué qu'il s'agit de la même formule que celle utilisée pour le calculateur de distance ? Et qu'elle découle directement de la géométrie – approfondissez vos connaissances avec le calculateur du théorème de Pythagore ?

4. Utilisez la formule algébrique du produit scalaire (la somme des produits des composantes des vecteurs) et substituez-la aux normes :

Sur le plan 2D :

Si les vecteurs $\boldsymbol{a}$ et $\boldsymbol{b}$ sont respectivement :

Et :

Sur le plan 3D:

Si les vecteurs $\boldsymbol{a}$ et $\boldsymbol{b}$ sont respectivement :

Et :

Donc :

Et le tour est joué !

Par ailleurs, si vos vecteurs sont sous une autre forme (vous connaissez leurs origines et extrémités), vous devrez effectuer quelques calculs au préalable. L'objectif est de les réduire à la notation vectorielle standard.

Si votre vecteur est décrit par son origine $A=(x_1, y_1)$ et son extrémité $B=(x_2, y_2)$, alors le vecteur$\boldsymbol{a}$ peut être exprimé comme suit :

Encore un peu flou ? Ne vous inquiétez pas ! Nous vous avons préparé quelques calculs à titre d'exemple pour que tout soit clair comme de l'eau de roche.

Supposons que vous vouliez trouver l'angle entre deux vecteurs :

et $\boldsymbol{b}$ défini comme le vecteur entre les points $A = (1, 1, 2)$ et $B = (-4, -8, 6)$.

Que devez-vous faire ?

1. Tout d'abord, calculez le vecteur $\boldsymbol{b}$, à l'aide de son origine et de son extrémité :

2. Ensuite, trouvez le produit scalaire des vecteurs $\boldsymbol{a}$ et $\boldsymbol{b}$ :

3. Ensuite, déterminez la norme des vecteurs :

Et :

4. Enfin, utilisez l'équation du produit scalaire transformé :

Et le tour est joué ! Vous venez de calculer l'angle entre deux vecteurs à 3 dimensions. Nous vous félicitons !

Si vous souhaitez apprendre d'autres concepts de la géométrie des coordonnées, nous vous recommandons de consulter le calculateur de taux de variation moyen 🇺🇸.

Alors, comment fonctionne notre calculateur d'angle entre deux vecteurs ? Suivez ces instructions étape par étape :

1. Choisissez votre espace vectoriel. Prenons le même exemple que dans le paragraphe précédent. Nos vecteurs et nos points ont trois coordonnées, nous devons donc choisir l'option 3D.

2. Choisissez la représentation du premier vecteur. Le premier vecteur est en notation standard, alors laissez la valeur par défaut : représentation par des coordonnées.

3. Entrez le premier vecteur. Saisissez $x = 3,$ $y = 6,$ et $z = 1$.

4. Choisissez la représentation du deuxième vecteur. Cette fois-ci, vous devez la remplacer par représentation par des points.

5. Entrez les valeurs du deuxième vecteur. Saisissez $\boldsymbol A = (1,1,2)$ et $\boldsymbol B = (-4,-8,6)$ dans les champs appropriés.

6. Le calculaateur affiche l'angle entre deux vecteurs 3D dès que vous avez rempli le dernier champ. Dans notre cas, il est de $150,\!2\degree$ – ce qui est, bien sûr, le même résultat que nous avons obtenu dans nos calculs à la main.

Un vecteur est un objet géométrique qui possède à la fois une norme et une direction. Il est très courant de les utiliser pour représenter des quantités physiques telles que la force, la vitesse et le déplacement, entre autres.

L'angle formé entre deux vecteurs est défini en utilisant l'inverse du cosinus du produits scalaire des deux vecteurs et du produit de leurs normes.

Calculer l'angle entre deux vecteurs dans un espace à 2 dimensions :

1. Trouvez le produit scalaire des vecteurs.
2. Divisez le produit scalaire par la norme du premier vecteur.
3. Divisez le résultat par la norme du second vecteur.

Mathématiquement, l'angle α entre deux vecteurs [x_a, y_a] et [x_b, y_b] peut s'écrire comme suit :

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))]

Calculer l'angle entre deux vecteurs dans un espace à 3 dimensions :

1. Trouvez le produit scalaire des vecteurs.
2. Divisez le produit scalaire par la norme du premier vecteur.
3. Divisez le résultat par la norme du second vecteur.

Mathématiquement, l'angle α entre deux vecteurs [x_a, y_a, z_a] et [x_b, y_b, z_b] peut s'écrire comme suit :

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²) )]