Calculateur d'angle au centre
Vous êtes-vous jamais demandé comment trouver l'angle au centre compris entre deux rayons d'un cercle ? Le calculateur d'angle au centre est là pour vous aider ! Les seules variables dont vous avez besoin sont la longueur de l'arc de cercle et le rayon.
Poursuivez votre lecture pour découvrir la définition de l'angle au centre et pour connaître sa formule.
Qu'est-ce que l'angle au centre d'un cercle ?
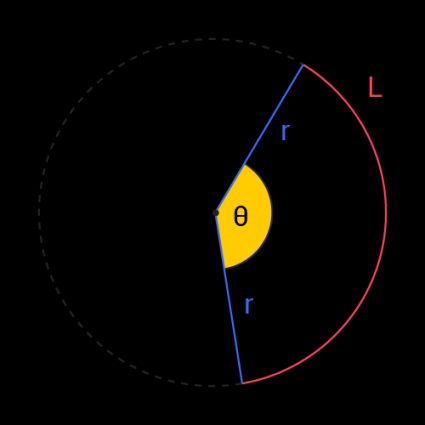
Un angle au centre est un angle délimité par deux rayons d'un cercle dont le sommet est situé au centre de ce cercle. Vous pouvez imaginer que l'angle au centre se trouve au milieu d'une grande pizza circulaire (là où il y a le plus de garniture), et que les bords d'une part sont les rayons délimitant cet angle.
Vous pouvez trouver l'angle au centre en utilisant la formule suivante :
où :
- – l'angle au centre en radians
- – la longueur de l'arc de cercle
- – le rayon
D'où vient la formule de l'angle au centre ?
La simplicité de la formule de l'angle au centre délimité par deux rayons vient de la définition du radian. Un radian est une unité d'angles, et un angle au centre délimité par des rayons égaux à la longueur de l'arc de cercle est égal à :
Exemple : l'angle au centre d'une pizza
Les maths peuvent donner faim, prenons donc un exemple avec une pizza pour mieux comprendre le concept d'angle au centre. Croyez-le ou non, les pizzas sont parfaites pour expliquer les opérations mathématiques liées aux cercles, comme vous pouvez le voir dans notre calculateur de taille de pizza 🇺🇸. Quel serait l'angle au centre entre deux bords d'une part de longueur si nous voulons que la croûte, , aie la même longueur que le rayon ?
Dans ce cas, , et nous savons qu'un angle au centre est égal à si . Par conséquent, l'angle au centre de notre part est égal à . Voici comment arriver à ce résultat en utilisant la formule de l'angle au centre :
Combien de parts de pizza ayant un angle au centre de 1 radian peut-on découper dans une pizza circulaire ?
Dans une pizza circulaire, l'angle au centre est égal à 2π radians (360°). , donc, nous pourrons découper parts ayant un angle au centre de , et une septième part de .
La même chose vaut pour la longueur de la croûte. Étant donné que la circonférence est égale à , nous effectuons le calcul suivant :
Par conséquent, nous pourrons découper parts dont la croûte a une longueur de , car .
Maintenant, si vous avez encore faim, jetez un œil au calculateur d'aire d'un secteur pour calculer l'aire de chaque part de pizza !
Défi : quelle est la distance parcourue par la Terre au cours de chaque saison ?
Pour résoudre ce problème, essayez d'utiliser le calculateur d'angle au centre dans l'autre sens. La Terre se trouve à environ 149,6 millions de kilomètres du Soleil. La Terre parcourt approximativement un quart de son orbite chaque saison. Combien de kilomètres parcourt-elle au cours d'une seule saison ?
Abordons ce problème étape par étape :
-
Simplifiez le problème en supposant que l'orbite de la Terre soit circulaire. (L'orbite de la Terre est en réalité elliptique et change constamment). Dans ce modèle, le Soleil est au centre du cercle, et l'orbite de la Terre en est la circonférence.
-
Le rayon est la distance entre la Terre et le Soleil : millions de km.
-
L'angle au centre est délimité par deux rayons formant un angle de (un quart de cercle) : .
-
Utilisez le calculateur d'angle au centre pour trouver la longueur de l'arc de cercle, c'est-à-dire la distance parcourue au cours d'une saison.
Vous pouvez tenter d'effectuer les calculs vous-même en réarrangeant la formule comme suit :
Convertissez ensuite l'angle au centre en radians : . (Utilisez notre calculateur de conversion d'angles 🇺🇸 si vous avez besoin d'un peu d'aide.) Et enfin, résolvez l'équation :
Si l'on suppose que l'orbite de la Terre est parfaitement circulaire, notre planète parcourt environ 234,9 millions de kilomètres au cours de chaque saison !
FAQ
Comment trouver l'angle au centre d'un cercle ?
Pour trouver l'angle au centre d'un cercle, utilisez la formule suivante :
θ = L / r
où :
θ– l'angle au centre en radiansL– la longueur de l'arc de cercler– le rayon du cercle
Pour trouver l'angle au centre délimité par deux rayons, vous devez calculer le rapport entre la longueur de l'arc de cercle et le rayon.
Vous pouvez imaginer que l'angle au centre se trouve à l'extrémité d'une part de pizza, et que l'angle est délimité par ses bords.
Comment trouver le rayon à partir de la longueur de l'arc de cercle et de l'angle au centre ?
Pour trouver le rayon d'un cercle à partir de la longueur de l'arc de cercle et de l'angle au centre, vous devez calculer le rapport entre la longueur de l'arc de cercle et l'angle au centre.