Calculateur d'aire d'un cercle
Sommaire
Formule de l'aire d'un cercle : comment calculer l'aire d'un cercle ?Calcul de la surface d'un cercle : comment utiliser le calculateur d'aire d'un cercle ?Pourquoi avons-nous besoin d'outils de calcul d'aire du cercle ?FAQLe calculateur d'aire d'un cercle vous permet de calculer l'aire d'un cercle avec le diamètre ou le rayon, ou on dira plutôt en fonction de son diamètre ou de son rayon. Notre outil fonctionne dans les deux sens – que vous cherchiez à calculer l'aire d'un cercle à partir de son rayon ou à trouver le rayon d'un cercle à partir de son aire, vous êtes au bon endroit. ◔
Nous allons vous donner un aperçu des informations les plus essentielles concernant l'aire d'un cercle, son diamètre et son rayon. Nous apprendrons comment calculer l'aire ou la superficie d'un cercle, nous parlerons de la formule de l'aire d'un cercle et nous discuterons des autres branches des mathématiques qui utilisent cette même équation.
Parfois, à la place de l'aire d'un cercle, certaines personnes parlent de la surface d'un cercle ; ce n'est pas mathématiquement correct, car l'aire correspond à la superficie d'un cercle et non à sa surface. Néanmoins, puisque c'est entré dans le langage courant, nous utiliserons aussi le terme surface d'un cercle pour parler de l'aire d'un cercle.
Ne tardez plus et essayez notre calculateur d'aire d'un cercle !
Formule de l'aire d'un cercle : comment calculer l'aire d'un cercle ?
Alors, examinons comment effectuer le calcul de la surface d'un cercle. Il existe plusieurs façons d'y parvenir. Ici, nous pouvons calculer la surface d'un cercle avec le diamètre ou le rayon, ou plutôt son aire si on veut être mathématiquement correct.
💡 Le diamètre est la ligne qui traverse le centre de la figure et touche ses deux bords. Le rayon commence au centre de la figure et se termine au bord de la figure.
Vous pouvez trouver le diamètre d'un cercle en multipliant le rayon d'un cercle par deux :
Diamètre = 2 × Rayon
La formule de calcul de l'aire d'un cercle en utilisant le rayon est la suivante :
Aire d'un cercle = π × r2
Et, la formule de calcul de l'aire d'un cercle en utilisant le diamètre est la suivante :
Aire d'un cercle = π × (d/2)2
où :
- π est approximativement égal à 3,14. Que vous souhaitiez calculer la surface d'un cercle avec le diamètre ou le rayon, vous devrez utiliser cette constante dans presque tous les cas.
🔎 Un autre aspect important des cercles est leur circonférence. Vous pouvez en apprendre davantage sur la circonférence et sa relation avec l'aire dans notre calculateur de formule du cercle.
Maintenant que vous savez comment calculer l'aire d'un cercle, nous vous invitons à explorer d'autres sujets qui lui sont liés.
- Circonférence et périmètre du cercle.
- Diagramme circulaire – aussi appelé diagramme en secteurs.
- Aire du cercle inscrit à l'intérieur d'un carré.
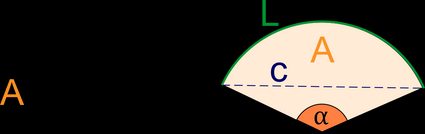
- Secteur d'un cercle – il s'agit d'une section d'un cercle comprise entre deux rayons. Vous pouvez l'assimiler à une gigantesque part de pizza.
Par ailleurs, pourquoi ne pas essayer nos autres calculateurs de cercles apparentés à notre calculateur d'aire d'un cercle :
-
Calculateur d'aire de segment d'un cercle 🇺🇸
C'est une partie « découpée » d'un cercle, limitée par une corde ou une sécante.
-
C'est un angle dont le sommet est au centre et dont les côtés s'étendent jusqu'à la circonférence.
Calcul de la surface d'un cercle : comment utiliser le calculateur d'aire d'un cercle ?
Vous pouvez calculer l'aire d'un cercle avec le diamètre ou le rayon, ainsi que déterminer le diamètre ou le rayon à partir de l'aire, à l'aide de notre calculateur de surface d'un cercle :
-
Déterminez si votre valeur donnée est un diamètre ou un rayon à l'aide de l'image de droite et des définitions disponibles dans la section ci-dessus (vous pouvez calculer l'aire d'un cercle en utilisant son diamètre aussi bien que son rayon).
-
Saisissez votre valeur dans le champ approprié du calculateur de superficie d'un cercle.
-
Cela n'a pas pris longtemps – vos résultats sont déjà là ! Nous avons décidé d'inclure la solution étape par étape et les données les plus importantes juste en dessous du calculateur d'aire d'un cercle.
Voilà comment calculer l'aire d'un cercle en un rien de temps. 😉
🔎 L'aire n'est pas la seule propriété liée au diamètre, la circonférence l'est aussi. Pour en savoir plus, consultez notre calculateur de circonférence en fonction du diamètre.
Pourquoi avons-nous besoin d'outils de calcul d'aire du cercle ?
L'aire du cercle – trouvée avec les calculateurs de rayon et de diamètre – sert de base à de nombreuses autres équations, non seulement en mathématiques, mais aussi dans la vie de tous les jours ! Voici quelques exemples où savoir comment trouver l'aire d'un cercle peut être utile !
-
Nous avons besoin de connaître l'aire d'un cercle pour calculer le volume d'un cône et sa surface. 🎉
-
Votre soirée pizza ne serait pas complète sans estimer la taille de la pizza basée sur le calculateur de diamètre en fonction de l'aire. 🍕
-
Nous utilisons des calculs similaires à celui-ci pour en savoir plus sur la sphère, comme son volume. 🌐
-
Vous aimez les belles robes ? Peut-être aimez-vous coudre ? Coudre efficacement des jupes circulaires n'a jamais été aussi facile. 👗
Comment calculer le diamètre d'un cercle à partir de l'aire ?
Les formules reliant le diamètre et l'aire d'un cercle se lisent aire = π × (diam/2)2 et diam = 2 × √(aire / π). Par exemple, le diamètre d'un cercle d'aire unitaire est approximativement égal à 1,128 car diam = 2 × √(1 / π) ≈ 1,128.
Quel est le rayon d'un cercle d'aire 10 ?
Le rayon est approximativement égal à 1,784. La réponse précise est √(10 / π). Pour obtenir ce résultat, rappelez-vous la formule : aire = π × r2. Nous la transformons sous la forme r2 = aire / π, et nous voyons ainsi que le rayon est égal à la racine carrée de aire / π. En introduisant aire = 10, nous obtenons :
rayon = √(10 / π) ≈ √(10 / 3,14) ≈ √3,185 ≈ 1,785.
Comment trouver la circonférence d'un cercle à partir de l'aire ?
Pour déterminer la circonférence d'un cercle à partir de son aire, procédez comme suit :
- Multipliez la surface par π.
- Prenez la racine carrée du résultat de l'étape 1.
- Multipliez par 2.
- Vous avez trouvé la circonférence du cercle à partir de son aire ! Bravo !
L'aire et la circonférence d'un cercle peuvent-elles être égales ?
Oui, l'aire et la circonférence d'un cercle ont la même valeur de 4π si le rayon du cercle a une longueur de 2. Rappelez-vous cependant que les unités sont différentes ! La circonférence a des unités de longueur, et l'aire a, eh bien, des unités d'aire.
La surface et le rayon d'un cercle peuvent-ils être égaux ?
Oui, prenez un cercle de rayon r = 1/π. Son aire est alors égale à πr2 = π(1/π)2 = 1/π, et a donc la même valeur que le rayon. Rappelez-vous cependant que les unités diffèrent ! Le rayon et l'aire ont respectivement des unités de longueur et d'aire ; par exemple, cm et cm².
