Calcul sur les vecteurs | Outil en ligne

Bienvenue sur notre outil de calcul sur les vecteur ! Il vous aidera à effectuer et à comprendre toute une série d'opérations sur les vecteurs. Avez-vous les coordonnées cartésiennes de deux vecteurs, ou connaissez-vous simplement leur direction et leur norme vectorielle ? Peut-être avez-vous besoin de trouver le vecteur entre deux points ? Cet outil de calcul sur les vecteur peut faire face à toutes ces situations ; il effectue :

• l'addition de vecteurs ;
• la soustraction de vecteurs ;
• la multiplication de vecteurs (produit vectoriel et produit scalaire); et
• les projections de vecteurs.

En prime, nous vous apprendrons également ce qu'est la norme d'un vecteur et comment normaliser un vecteur.

Dans un système cartésien, nous décrivons le vecteur a dans un plan 2D par ses coordonnées cartésiennes :

a = [a_x, a_y]

Ces coordonnées correspondent au fait que nous pouvons décomposer un déplacement le long du vecteur a en un déplacement horizontal a_x le long de l'axe x et un déplacement vertical a_y le long de l'axe y.

De même, nous décrivons les vecteurs dans l'espace 3D en utilisant le système cartésien xyz à trois nombres :

a = [a_x, a_y, a_z]

qui correspondent aux déplacements le long des axes x, y et z, respectivement.

Nous pouvons également décrire un vecteur en termes de direction et de norme du vecteur. La norme d'un vecteur est sa longueur et la direction d'un vecteur est l'angle entre l'axe des abscisses et le vecteur.

Soit [a_x, a_y] les coordonnées cartésiennes d'un vecteur de norme d'un vecteur de norme m et de direction θ. Pour convertir un ensemble de coordonnées en l'autre, utilisez les formules suivantes :

a_x = m × cos(θ)

a_y = m × sin(θ)

Si vous devez calculer un vecteur entre deux points, c'est-à-dire à partir du point initial et du point final, il suffit de soustraire les coordonnées du point final du point initial :

• Point initial (origine) : a = [a_x, a_y, a_z]

• Point final : b = [b_x, b_y, b_z]

• Vecteur entre ces deux points :

  [b_x - a_x, b_y - a_y, b_z - a_z]

Voyons un exemple :

• Point initial : [1, 2, 3]

• Point final : [1, 1, -1]

• Vecteur entre ces deux points :

  [1 - 1, 1 - 2, 3 - (-1)] = [0, -1, 4]

La normalisation d'un vecteur consiste simplement à comprimer/étirer un vecteur de manière à ce que sa norme soit la même. N'oubliez pas que la direction d'un vecteur doit être conservée !

Pour normaliser un vecteur, trouvez sa norme en utilisant le théorème de Pythagore. La norme d'un vecteur est sa magnitude : la racine carrée de la somme des coordonnées élevées au carré de votre vecteur. Divisez ensuite chaque coordonnée du vecteur initial par cette norme. Vous pouvez également utiliser le calculateur de norme d'un vecteur 🇺🇸 pour trouver la norme, qui est la version la plus simple de ce calculateur de vecteur.

Exemple :

Soit a = [2, 3, 4]. Trouvons la norme de a :

|a| = √(4 + 9 + 16) = √29

La normalisation de a nous donne le vecteur a/|a| = [2/√29, 3√29, 4/√29]. Savez-vous que nous disposons d'un calculateur dédié à la normalisation des vecteurs 🇺🇸 ?

Pour utiliser l'outil de calcul sur les vecteurs, il suffit de suivre les étapes ci-dessous :

1. Indiquez si vous travaillez avec des vecteurs à 2 dimensions ou des vecteurs à 3 dimensions.
2. Décidez de l'opération vectorielle que vous voulez effectuer. Vous pouvez choisir l'addition ou la soustraction de vecteurs, la multiplication de vecteurs (produit scalaire ou vectoriel), la normalisation, la projection de vecteurs ou la recherche du vecteur entre deux points.
3. Entrez vos données. Vous pouvez choisir entre les coordonnées cartésiennes ou la direction et la norme du vecteur dans le cas de vecteurs plans.
4. Notre calculateur de vecteurs affiche les résultats immédiatement. Amusez-vous bien ! 😊

• En coordonnées cartésiennes, nous pouvons effectuer une addition de vecteurs 🇺🇸 en ajoutant simplement les composantes correspondantes des vecteurs.

  Pour a = [a_x, a_y, a_z] et b = [b_x, b_y, b_z],

  On a a + b = [a_x + b_x, a_y + b_y, a_z + b_z].

  Exemple :

  La somme de a = [2, 3, 4] et b = [1, -2, 3] est :

  a + b = [2 + 1, 3 + (-2), 4 + 3] = [3, 1, 7]

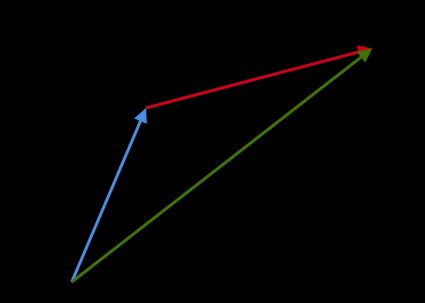
• Méthode graphique : pour deux vecteurs a et b, si l'on veut obtenir la somme vectorielle a + b, on place l'origine de b à l'extrémité de a. Le vecteur résultant va de l'origine de a à la pointe de b. Nous appelons cette règle la loi du parallélogramme :

La soustraction du vecteur b du vecteur a est juste l'addition de -b à a. Pour trouver le vecteur -b, prenez les coordonnées de b avec des signes opposés ; remplacez les plus par des moins et les moins par des plus.

Si b = [1, -2, 4], alors -b = [-1, 2, -4].

• Par conséquent, en coordonnées cartésiennes, on effectue la soustraction vectorielle a - b en soustrayant les coordonnées de b à celles de a.

  Si a = [a_x, a_y, a_z] et b = [b_x, b_y, b_z],

  alors a - b = [a_x - b_x, a_y - b_y, a_z - b_z].

  Exemple :

  La différence de a = [2, 3, 4] et b = [1, -2, 3] est donnée par :

  a - b = [2 - 1, 3 - (-2), 4 - 3] = [1, 5, 1]

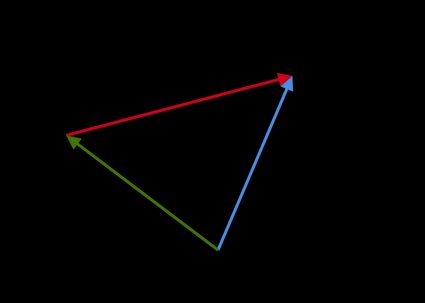
• Méthode graphique : on obtient la différence vectorielle a - b en plaçant la pointe de b à la pointe de a et en dessinant un vecteur de l'origine de a à l'origine de b :

Soyez prudent lorsqu'on vous demande de multiplier des vecteurs : il existe plusieurs types de multiplication vectorielle ! Les plus populaires sont le produit vectoriel et le produit scalaire, que nous décrivons ci-dessous :

Produit vectoriel

Le produit vectoriel est une opération désignée par l'opérateur × et prend deux vecteurs et renvoie un autre vecteur.
La formule est la suivante :

a × b = |a| × |b| × sin(θ) × n,

où :

• θ – angle entre a et b
• |a| et |b| – normes de a et b
• n – vecteur unitaire perpendiculaire à a et b, déterminé par la règle de la main droite.

Règle de la main droite :

Placez votre main droite de façon à ce que votre index pointe le long du vecteur a et votre majeur pointe le long du vecteur b : votre pouce montre la direction du produit vectoriel a × b.

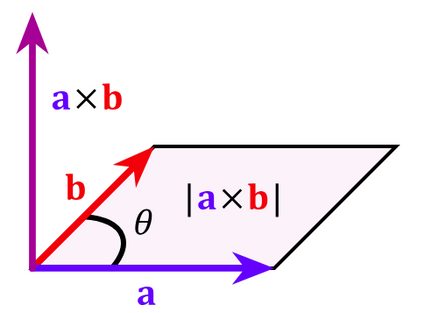
• Interprétation graphique : Le vecteur résultant a × b forme un angle droit (perpendiculaire) avec les vecteurs initiaux, et sa norme est égale à l'aire d'un parallélogramme traversé par les vecteurs initiaux.

• En termes de coordonnées cartésiennes :

  pour a = [a_x, a_y, a_z],

  et b = [b_x, b_y, b_z], on a

  a × b = [a_y×b_z - a_z×b_y, a_z×b_x - a_x×b_z, a_x×b_y - a_y×b_x].

  Exemple :

  Le produit vectoriel de a = [2, 3, 4] et b = [1, -2, 3] est égal à :

  a × b = [3 × 3 - 4 × (-2), 4 × 1 - 2 × 3, 2 × (-2) - 3 × 1] = [17, -2, -7]

• Oui, la formule semble un peu intimidante. Il est plus facile de s'en souvenir une fois que vous avez réalisé que les coordonnées du produit sont les déterminants des matrices 2 × 2 appropriées :

1. La première coordonnée est :

2. La deuxième coordonnée est :

3. La troisième coordonnée est :

• Soyez prudent·e avec l'ordre des vecteurs, car contrairement au produit scalaire, l'ordre compte pour le produit vectoriel ! Plus précisément, nous avons b × a = - a × b, donc si vous vous êtes trompé dans l'ordre, changez simplement le signe, et tout ira bien 🙃

• Le produit vectoriel a beaucoup d'applications en physique et en ingénierie : par exemple, vous pouvez l'utiliser pour déterminer la force électromagnétique 🇺🇸. Consultez notre calculateur de produit vectoriel pour en savoir plus !

Produit scalaire

Le produit scalaire est une opération désignée par l'opérateur · qui prend deux vecteurs et renvoie un nombre. Pour deux vecteurs a et b, leur produit scalaire est le produit de leurs normes |a| et |b| et le cosinus de l'angle θ entre eux :

a - b = |a| × |b| × cos(θ)

• En coordonnées cartésiennes, le produit scalaire est la somme des produits des coordonnées correspondantes de vos deux vecteurs :

  a - b = a_x × b_x + a_y × b_y + a_z × b_z**

  Exemple :

  Le produit scalaire de a = [2, 3, 4] et b = [1, -2, 3] est :

  a - b = 2 × 1 + 3 × (-2) + 4 × 3 = 2 - 6 + 12 = 8

• Comme vous l'avez peut-être déjà deviné à partir de la formule, l'ordre n'a pas d'importance ici : a - b = b - a.

• Astuce : si vous calculez le produit scalaire d'un vecteur avec lui-même, vous obtenez la norme du vecteur au carré : a - a = |a|² !

• Pour plus de détails, consultez notre calculateur du produit scalaire d'un vecteur 🇺🇸.

La projection de b sur a est le vecteur qui est la meilleure approximation de b parmi les vecteurs obtenus en étirant et en comprimant le vecteur a. Par conséquent, pour trouver la projection, il vous suffit de connaître le facteur d'étirement et d'écrasement approprié.

• Formule :

  La projection de b sur a est le vecteur a mis à l'échelle par :

  a - b / |a|²

  Exemple :

  Soit a = [2, 3, 4] et b = [1, -2, 3]. Calculons la projection de b sur a. Tout d'abord, trouvons le facteur d'échelle. Nous avons calculé ci-dessus que a - b = 8 et |a| = √29. Par conséquent, la projection de b sur a est :

  8/29 × [2, 3, 4] = [16/29, 24/29, 32/29]

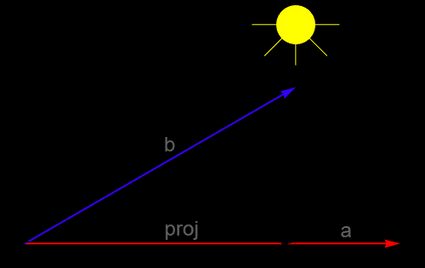
• Pour trouver la projection de b sur a graphiquement, vous devez décomposer b le long des axes traversés par a et perpendiculaires à a. La composante qui se trouve le long de a est la projection de b sur a. Vous pouvez aussi l'imaginer comme l'ombre que le vecteur b projetterait sur le vecteur a si une source lumineuse était suspendue au-dessus de ces vecteurs :

Pour en savoir plus sur la projection de vecteurs sur d'autres vecteurs, consultez notre calculateur de projection d'un vecteur 🇺🇸.