Calculadora de frecuencia

La calculadora de frecuencia te permite hallar rápidamente la frecuencia de una onda, dado su período o su longitud de onda y velocidad de propagación. Incluso, puedes elegir una velocidad de propagación de la lista predefinida, para que no tengas que acordarte.

En el texto también encontrarás la definición de frecuencia, dos fórmulas de frecuencia (para convertir periodo a frecuencia y longitud de onda a frecuencia) y algunos ejemplos que muestran cómo calcular la frecuencia.

Si quieres saber más sobre las ondas, consulta la calculadora de longitud de onda, y, si quieres conocer la frecuencia de las notas musicales, consulta la calculadora de frecuencia de notas 🇺🇸.

Echa un vistazo al siguiente modelo de una onda; te ayudará a entender los términos utilizados en la definición de frecuencia que aparece a continuación.

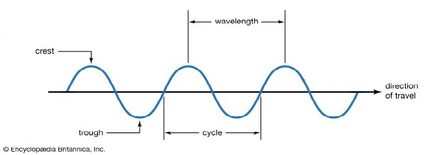
La frecuencia es el número de ciclos de onda completos por segundo. En otras palabras, la frecuencia nos indica cuántas crestas de onda pasan por un punto determinado en un segundo.

Esta definición de frecuencia nos lleva a la fórmula de frecuencia más sencilla:

$f$, denota la frecuencia, y $T$, el tiempo que tarda en completarse un ciclo de onda medido en segundos.

La unidad de frecuencia del SI es el hercio (Hz), que equivale a 1/s (un ciclo por segundo). Otras unidades de frecuencia son el milihercio (mHz), el kilohercio (kHz), el megahercio (MHz), el gigahercio (GHz) y el terahercio (THz).

Observemos otra imagen que nos permitirá ver la relación entre frecuencia y longitud de onda. La longitud de onda es la distancia entre dos crestas (o valles) adyacentes. En otras palabras, es la longitud de un ciclo de onda. Cuanto mayor es la longitud de onda, menor es la frecuencia:

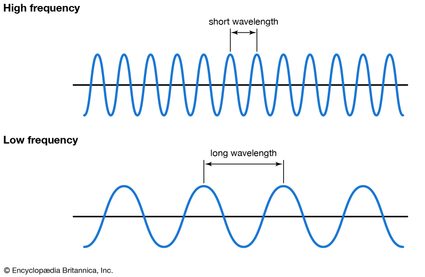
Otro dato que necesitamos es la velocidad a la que viajan las ondas (velocidad de propagación o velocidad de fase), la cual determina cuántas de ellas pasarán cada segundo por un punto determinado. Esto significa que cuanto mayor sea la velocidad de la onda, mayor será la frecuencia.

Estas dos relaciones entre frecuencia y longitud de onda ($\lambda$), y entre frecuencia y velocidad ($v$), nos llevan a la siguiente ecuación de frecuencia:

Nuestra calculadora de frecuencia incorpora las fórmulas de frecuencia previamente mencionadas. Por lo tanto, puedes usarla como calculadora de periodo a frecuencia o como calculadora de longitud de onda a frecuencia.

Cómo usarla como calculadora de período a frecuencia (hallar la frecuencia dado el periodo):

1. Introduce el tiempo en el que se produce un ciclo de onda (periodo). La calculadora determinará la frecuencia.

2. También puedes usar esta calculadora para determinar el periodo si conoces su frecuencia.

Cómo usarla como calculadora de longitud de onda a frecuencia (calcular la frecuencia a partir de la longitud de onda):

1. Elige el tipo de onda y su medio en la lista del primer campo. Por defecto, lo tenemos configurado como luz en el vacío. Si seleccionas la opción “Establecer una velocidad de onda personalizada”, puedes introducir una velocidad de onda de tu elección.

2. Introduce la longitud de onda y aparecerá el valor de la frecuencia.

Así que, básicamente, puedes introducir dos variables cualesquiera, y la tercera aparecerá inmediatamente 😀

Para resolver cualquier duda acerca de cómo calcular la frecuencia a partir del periodo, analicemos algunos ejemplos sencillos. En primer lugar, recordemos la ecuación de la frecuencia:

Ejemplo 1:

Cómo hallar la frecuencia de una onda en la que un ciclo se completa en 0.25 s:

Recuerda convertir $\frac{1}{\text{s}}$ a la unidad de frecuencia:

Ejemplo 2:

Cómo hallar la frecuencia de una onda en la que se producen 360 ciclos en 1 minuto:

En esta ocasión, queremos aprender a hallar la frecuencia de una onda si nos dan la velocidad de propagación y la longitud de onda. Para eso, tienes que utilizar la siguiente fórmula de frecuencia:

Ejemplo 1:

La velocidad de propagación es igual a 320 m/s, y la longitud de onda es de 8 m. Al hallar la frecuencia, obtenemos:

Ejemplo 2:

Hallar la frecuencia de la luz si la longitud de onda es igual a 3000 km. La velocidad de propagación es igual a la velocidad de la luz en el vacío, aproximadamente igual a $300\ 000\ \tfrac{\text{km}}{\text{s}}$. Utilizando la fórmula de la frecuencia, obtenemos:

En comunicación inalámbrica, existe un volumen elipsoidal entre la antena emisora y la antena receptora. Esta región viene determinada por la distancia entre las antenas y la frecuencia de la onda inalámbrica. Se denomina zona de Fresnel y tiene el siguiente aspecto:

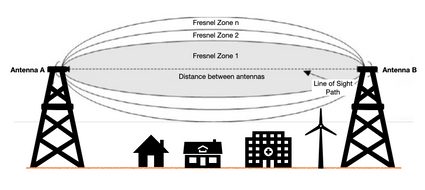
De la fórmula principal de la zona de Fresnel se deduce que cuanto mayor sea la frecuencia, menor será el volumen elipsoidal necesario para que la comunicación inalámbrica sea correcta. Por el contrario, para una frecuencia baja, obtenemos una zona de Fresnel mayor que los edificios o árboles podrían bloquear fácilmente y, por tanto, producir una comunicación inalámbrica inestable.

Cuando dos ondas de frecuencias distintas interfieren entre sí de forma constructiva y destructiva, producen un patrón de interacción llamado batimiento o latido. Puedes encontrar la frecuencia específica de un latido con la calculadora de frecuencia de batimiento 🇺🇸 de Omni.

Otro fenómeno interesante debido a la interacción de ondas con frecuencias diferentes es la resonancia. La resonancia puede producirse, por ejemplo, cuando el aire atraviesa una cavidad, como al soplar el cuello de una botella vacía.

Esta cavidad resonante se conoce como resonador de Helmholtz. Si cambia el volumen de la cavidad, cambia la frecuencia de resonancia. Puedes determinar la frecuencia de resonancia de cavidades con distintos volúmenes utilizando nuestra calculadora de resonador de Helmholtz 🇺🇸.