Calculadora de pagos de préstamo

La calculadora de pagos de préstamos es una herramienta muy útil para calcular los pagos mensuales (o de cualquier otra frecuencia) necesarios tras contratar un préstamo que requiere pagos iguales. Por ejemplo, puedes calcular las cuotas de tu automóvil o de tu crédito hipotecario. También te presentamos la fórmula de pago de un préstamo y te presentamos una guía práctica que te ayudará a comprender cómo calcular las cuotas mensuales de un préstamo.

Además, puedes leer qué es un calendario de pagos de préstamos para que veas en detalle cómo se construyen los pagos de un préstamo.

Si estás buscando préstamos, puedes consultar nuestra calculadora de comparación de préstamos 🇺🇸, que puede darte una excelente ayuda para elegir la opción más favorable. O, si estás pensando en suspender la amortización, puedes aplicar nuestra calculadora de pago aplazado 🇺🇸 para ver cómo afectaría el aplazamiento del préstamo a tus costes y a tu calendario.

Cuando estás planeando una compra, pero te das cuenta de que no puedes permitírtela con tus ahorros o ingresos (o bien, estás a punto de tomar una decisión de inversión que requiere apoyo financiero), la forma más directa de obtener el dinero necesario es acudir a un banco para pedir un préstamo. Si te encuentras en esta situación, probablemente una de las primeras cosas que te venga a la cabeza es si podrás hacer frente a los pagos (o cuotas) requeridos con tus ingresos. Para resolver este enigma, debes responder a la pregunta crucial: ¿cuál será la cuota de mi préstamo?

Con nuestra calculadora de pagos de préstamos, podrás calcular rápidamente la cantidad de dinero que necesitas dedicar a la devolución del préstamo durante un periodo de pago. Este dispositivo también te dará la cantidad total que tienes que devolver durante todo el plazo del préstamo. También puedes utilizarla para calcular el importe del préstamo a partir de los pagos del mismo.

Antes de seguir adelante, es esencial que hablemos de algunos términos específicos que puedes encontrarte cuando te plantees pedir un préstamo. A continuación, podrás familiarizarte con estas frases para comprender mejor el concepto de préstamo.

• Importe del préstamo: es la cantidad de dinero (también conocida como principal) que un banco (o cualquier otra institución financiera) presta o, a la inversa, que un particular toma prestada. En otras palabras, es la cantidad que el prestatario se compromete a pagar al prestamista cuando venza el préstamo, sin incluir los intereses. Si quieres saber más sobre el cálculo de intereses, visita nuestra calculadora de interés simple.

• Tipo anual: es el tipo de interés (también llamado tipo nominal o tipo cotizado) que cotizan los bancos (u otras partes). También es importante tener en cuenta la tasa de inflación prevista cuando inspeccionas un tipo cotizado: cuanto mayor sea la tasa de inflación, menor será el tipo de interés real; por tanto, la carga real generada por el tipo de interés disminuye. Para saber más sobre la inflación, visita nuestra calculadora de inflación 🇺🇸.

• Plazo de amortización: en nuestro contexto, se refiere al plazo que durará el préstamo si sólo haces los pagos mínimos requeridos cada mes. Por ejemplo, una hipoteca a tipo fijo a 20 años tiene un plazo de 20 años calculadora de hipotecas 🇺🇸. Los préstamos para automóviles suelen tener plazos de 5 ó 6 años.

• Plazo de pago: se refiere al periodo concreto durante el cual el prestatario está obligado a realizar los pagos del préstamo.

• Tipo periódico: es la tasa de interés que cobra un prestamista o paga un prestatario en cada periodo de pago. Puede ser anual (en este caso, equivale al tipo anual), semianual, por trimestre, por mes, por día, o por cualquier otro intervalo de tiempo. Por ejemplo, un banco puede cobrar un 2% mensual en sus préstamos sobre tarjetas de crédito, o puede cobrar un 1% trimestral en sus préstamos. Para obtener la tasa de interés periódica, tienes que dividir la tasa anual por el número de pagos en un año. Por ejemplo, en el caso de un pago mensual con una tasa anual del 6%, la tasa de interés periódica es igual a 6% / 12 = 0.5%.

• Cuota del préstamo: es la cantidad de dinero que debe devolver el prestatario en cada periodo de pago. En la mayoría de los casos el dinero prestado se devuelve en pagos (cuotas) del préstamo en cantidades iguales a lo largo del plazo de pago. Este tipo de construcción del préstamo se denomina préstamo amortizado.

• Cronograma de pagos del préstamo/Cronograma de amortización: cada pago del préstamo consta de dos partes: una parte de interés y otra de devolución del capital. La parte de intereses es mayor al principio del plazo del préstamo, pero disminuye a medida que se reduce el saldo del préstamo. En otras palabras, cuanto más se haya devuelto del préstamo, mayor será la parte del capital en una cuota.

Tras hacer un rápido recorrido por la terminología financiera, podemos construir la fórmula de pago del préstamo aplicada en nuestra calculadora de préstamos.

Pago periódico del préstamo = Importe del préstamo / (((1 + Tipo periódico) ^ Número de pagos) - 1) / (Tipo periódico × ((1 + Tipo periódico) ^ Número de pagos)).

Es importante tener en cuenta que la fórmula de pago del préstamo anterior se basa en la construcción amortizada del préstamo con pagos iguales en los que los importes de interés se calculan después del capital impagado. El otro tipo de construcción del préstamo se basa en el interés compuesto, en el que los importes de interés se añaden al saldo de capital después de cada periodo específico correspondiente a la frecuencia de capitalización.

Ahora, mientras te familiarizas con la jerga financiera utilizada en la construcción de préstamos y con la fórmula de pago de préstamos, vamos a ver cómo calcular los pagos de un préstamo mediante un sencillo ejemplo. Supongamos que estás a punto de comprarte un automóvil nuevo, y tus ahorros no son suficientes para pagar el precio total. Para obtener la cantidad que te falta, decides acudir a un banco que te ofrece un préstamo personal de 10.000 dólares con un interés del 6%, reembolsado mensualmente en 5 años. Puedes introducir fácilmente estos datos en nuestra calculadora:

• Importe del préstamo $10,000
• Tipo de interés anual: 6%
• Número de años: 5
• Frecuencia: mensual (Número de pagos en un año = 12)

Tasa periódica = Tasa anual / Número de pagos en un año = 0.06 / 12 = 0.005 = 0.5%.

Número de pagos = Número de años × Número de pagos al año = 5 × 12 = 60.

Podemos emplear la fórmula de pago del préstamo indicada anteriormente utilizando los valores anteriores.

Pago periódico del préstamo = Importe del préstamo / (((1 + Tipo periódico) ^ Número de pagos) - 1) / (Tipo periódico × ((1 + Tipo periódico) ^ Número de pagos)) = 10 000 / (((1 + 0.005) ^ 60) - 1) / (0.005 × ((1 + 0.005) ^ 60)) = $193.33

Después de calcular el pago periódico del préstamo, puedes tener una visión mucho mejor de tus obligaciones futuras, que te ayudarán a decidir si puedes hacer frente a la devolución del préstamo.

Además, puedes utilizar nuestra calculadora de préstamos para calcular el importe del préstamo o el pago total del préstamo a partir de las cuotas periódicas.

Supongamos que la cuota mensual de tu préstamo es de 100 dólares con un tipo anual del 9 por ciento y un plazo de pago de dos años.

• Cuota periódica del préstamo: 500 dólares
• Tipo anual: 9%
• Número de años: 2
• Periodicidad: mensual

Tipo periódico = Tipo anual / Número de pagos en un año = 0.09 / 12 = 0.0075 = 0.75%.

Número de pagos = Número de años × Número de pagos al año = 2 × 12 = 24.

importe del préstamo = Cuota periódica del préstamo × (((1 + Tipo periódico) ^ Número de pagos) - 1) / (Tipo periódico × ((1 + Tipo periódico) ^ Número de pagos)) = 500 × (((1 + 0.0075) ^ 24) - 1) / (0.0075 × ((1 + 0.0075) ^ 24)) = 10 944.5.

Pago total del préstamo = Número de pagos × Pago periódico del préstamo = 24 × 500 = 12 000 $.

Como ya hemos dicho, la mayoría de los préstamos se reembolsan en pagos iguales (cuotas) a lo largo de un tiempo determinado: los préstamos así construidos se denominan préstamos amortizados. Cada pago periódico consiste en una proporción cambiante de intereses y capital en la que el pago de intereses es decreciente y el pago de capital aumenta a lo largo del plazo de pago. La tendencia decreciente de la parte de intereses corresponde a la reducción del saldo pendiente del préstamo (saldo inicial). El calendario de pagos del préstamo (o calendario de amortización) representa una tabla detallada de los pagos periódicos del préstamo, mostrando el importe del capital y el importe de los intereses que constituyen cada pago hasta que el préstamo se liquida al final de su plazo.

La mejor forma de comprender mejor este tema es tomar un ejemplo práctico. La tabla siguiente representa el calendario de pagos de un préstamo hipotecario de 500.000 dólares a 20 años, reembolsado anualmente con un tipo anual del 5 por ciento. En este caso, la cuota anual del préstamo es de 40 121.29 dólares.

Esperemos que, al observar las tendencias del gráfico siguiente, comprendas mejor qué es la amortización.

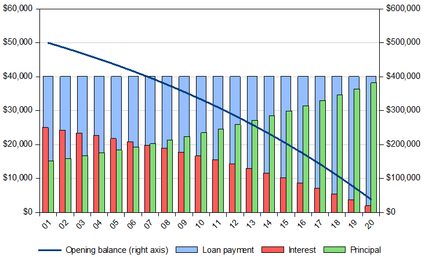
El saldo inicial de cada año representa el saldo pendiente (el importe del préstamo que hay que pagar). Como los pagos de intereses son relativamente altos al principio del plazo del préstamo, la parte del capital es pequeña durante los primeros periodos; así, el saldo pendiente disminuye lentamente. Sin embargo, a medida que disminuyen los saldos iniciales, los pagos de intereses también se reducen gradualmente, lo que da lugar a una parte creciente de las amortizaciones del capital. El mayor capital, a su vez, aumenta el ritmo de reducción del saldo inicial de cada periodo.