Kreisdiagramm Rechner
In der Mathematik hilft dir der Kreisdiagramm-Rechner dabei, die Datenverteilung (siehe Häufigkeitsverteilung Rechner 🇺🇸) in Form eines Kreisdiagramms zu visualisieren. Wenn du das Kreisdiagramm berechnest, kannst du den prozentualen Anteil jeder Art von Daten in deinem Datensatz sehen. Wir können auch die Wahrscheinlichkeit (siehe Wahrscheinlichkeitsrechner) im Kreisdiagramm berechnen, um Muster in den Daten zu erkennen.
Wie berechne ich ein Kreisdiagramm?
Kreisdiagramme basieren auf den Prozentsätzen jeder Art von Daten im Datensatz. Um ein Kreisdiagramm zu erstellen, listest du zuerst die Werte in den verschiedenen Segmenten des Datensatzes auf und gehst dann folgendermaßen vor:
- Finde die Gesamtsumme aller Werte im Datensatz.
- Teile den Wert jedes Segments durch die Gesamtsumme, um den entsprechenden Prozentsatz der Gesamtsumme für das Diagramm zu erhalten.
- Multipliziere diesen Prozentsatz mit 360°, um die Gradzahl für das Segment des Diagramms zu berechnen.
- Erstelle einen Sektor mit diesem Gradmaß im Kreisdiagramm.
- Mache das Gleiche für jedes Segment, um die Abbildung erfolgreich in unterschiedliche Sektoren zu unterteilen, die den verschiedenen Segmenten entsprechen! 🎉
Dadurch können wir verstehen, was ein Kreisdiagramm ist und die dazugehörigen Formeln, die uns sagen, wie wir Winkelgrade im Kreisdiagramm berechnen können. Ähnlich wie das Balkendiagramm 📊, das Histogramm (vgl. Histogramm Rechner 🇺🇸) und viele andere Diagrammtypen ist ein Kreisdiagramm ein mathematisches Werkzeug zur Datenvisualisierung. Sobald wir den prozentualen Anteil an der Gesamtsumme berechnet haben, wird die Abbildung darauf basierend erstellt.
Wie erstelle ich ein Kreisdiagramm? Ein Beispiel
Um ein Kreisdiagramm mit unserem Rechner zu erstellen, nehmen wir folgende Werte an:
Gruppen | Werte |
|---|---|
A | 20 |
B | 80 |
C | 20 |
D | 50 |
E | 30 |
Die Gesamtsumme aller Werte in dieser Beispieltabelle des Kreisdiagramms ist 200. Der Rechner bestimmt zunächst den prozentualen Anteil jedes Wertes an der Gesamtsumme und für das Sektordiagramm den entsprechenden Mittelwinkel des Sektors. Sobald wir den Winkel für die Sektoren erhalten haben, entsteht das Kreisdiagramm 🔵. Es wird dafür in Sektoren unterteilt, die den einzelnen Datensegmenten entsprechen.
Die entsprechenden Winkelgrade zu unserem Beispiel sind:
Gruppen | Werte | Prozent | Grad |
|---|---|---|---|
A | 20 | 10% | 36° |
B | 80 | 40% | 144° |
C | 20 | 10% | 36° |
D | 50 | 25% | 90° |
E | 30 | 15% | 54° |
Mit diesen Prozent- und Gradwerten erstellt der Kreisdiagramm-Rechner die Abbildung wie folgt:
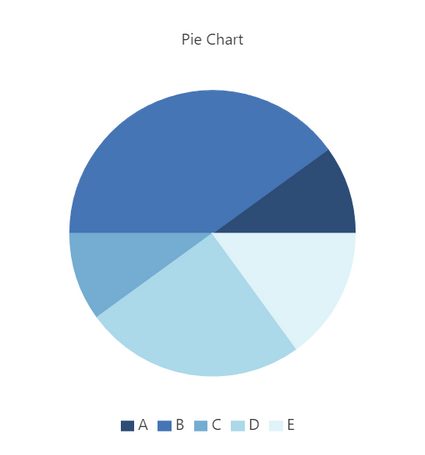
Dieses Beispiel zeigt uns, wie man mit dem Rechner die Winkel des Kreisdiagramms berechnet. Das hilft uns, zu verstehen, wie man ein Kreisdiagramm erstellt.
Wie berechne ich den Prozentsatz für ein Kreisdiagramm?
Um zu verstehen, wie man den Prozentsatz für ein Kreisdiagramm berechnet, gehen wir wie folgt vor:
- Finde die Summe aller Werte über alle Segmente der Daten.
- Dividiere den Wert jedes Segments durch die Summe, um den Dezimalwert zu erhalten.
- Wandle den Dezimalwert in einen Prozentsatz um, indem du ihn mit
100%multiplizierst 💯!
Wenn die Daten zum Beispiel nur zwei Arten von Segmenten haben, die jeweils die Hälfte der Gesamtwerte ausmachen, wird jedes dieser Segmente als Halbkreis in der Abbildung dargestellt, da es jeweils 50% der Gesamtwerte ausmacht.
FAQs
Wie berechne ich die Winkel für ein Kreisdiagramm?
Um den Winkel im Kreisdiagramm zu berechnen, müssen wir jeden Prozentsatz mit 360° multiplizieren. Sobald wir diesen Winkel im Kreisdiagramm berechnet haben, können wir einen Sektor mit diesem Winkel markieren, um den Teil der Abbildung zu kennzeichnen, der zu diesem Datensegment gehört.
Wie berechne ich die Wahrscheinlichkeit in einem Kreisdiagramm?
Der Kreisdiagramm-Rechner verwendet Prozentsätze, um den Zentralwinkel jedes Sektors in der Abbildung zu berechnen. Mit diesen Prozentsätzen können wir die Wahrscheinlichkeit jedes Datensegments ermitteln, indem wir sie einfach in einen Dezimalwert umwandeln! Wenn zum Beispiel ein Datensegment einen Sektor einnimmt, der 40 % der gesamten Abbildung ausmacht, ist die Wahrscheinlichkeit dieses Datensegments 0,4.
Was ist ein 75-25 Kreisdiagramm?
Wenn wir bei der Berechnung eines Kreisdiagramms mit 2 Datensegmenten 75% für das eine Datensegment und die restlichen 25% für das andere Datensegment erhalten, erhalten wir ein 75-25-Kreisdiagramm, bei dem drei Viertel ein Segment darstellen und ein Viertel das andere Segment darstellt. Das 75-25-Kreisdiagramm bedeutet, dass das Kreisdiagramm im Verhältnis 75:25 oder 3:1 zwischen den beiden Segmenten aufgeteilt wird.
Was sind 15 Prozent in einem Kreisdiagramm?
Um 15 Prozent in einem Kreisdiagramm zu berechnen, tue Folgendes:
- Multipliziere 15% mit 360°.
- So erhältst du 54°.
- Das heißt, wenn wir ein Datensegment mit 15 Prozent der Gesamtwerte haben, wird das im Kreisdiagramm als ein Sektor mit einem Zentralwinkel von 54° dargestellt.
Was sind 45% in einem Kreisdiagramm?
Es ist ein Sektor mit einem Zentralwinkel von 162°. Um zu wissen, was 45% in einem Kreisdiagramm sind, müssen wir Folgendes tun:
- Wir müssen den Prozentsatz mit 360° multiplizieren.
- So erhalten wir 162°.
- Dies wird im Kreisdiagramm als ein Sektor dargestellt, der etwas kleiner als ein Halbkreis ist.
Wie kann man 5% von 420 in einer Abbildung darstellen?
5% von 420 sind 21. Um dies in einem Kreisdiagramm zu visualisieren, finden wir 5% von 360°, was 18° ergibt. Dieses Ergebnis bedeutet, dass ein Datensegment, das 5 Prozent von 420 (oder der Gesamtzahl) ausmacht, im Kreisdiagramm mit einem Sektor mit einem zentralen Winkel von 18° dargestellt wird.