Zuletzt aktualisiert: 30. Oct 2024

Zylinder Volumen Rechner

Q: Wo gibt es Zylinder in der Natur?

Zylinder sind überall um uns herum , und wir reden nicht nur von Pringles-Dosen. Obwohl die Dinge in der Natur selten perfekte Zylinder sind, sind einige Beispiele dafür Baumstämme und Pflanzenstämme, einige Knochen (und damit Körper) und die Geißeln von mikroskopischen Organismen. Diese machen einen großen Teil der natürlichen Objekte auf der Erde aus!

Q: Wie berechnest du das Verhältnis von Oberfläche zu Volumen eines Zylinders?

Finde das Volumen des Zylinders mithilfe der Formel πr²h . Bestimme den Flächeninhalt des Zylinders mit der Formel 2πrh + 2πr² . Bilde ein Verhältnis aus den beiden Formeln, d.h. πr²h / 2πrh + 2πr² . Alternativ kannst du die Formel auch zu rh / 2(h+r) vereinfachen . Dividiere beide Seiten durch eine der Seiten, um das Verhältnis in seiner einfachsten Form zu erhalten.

Q: Wie kannst du die Höhe eines Zylinders bestimmen?

Wenn du das Volumen und den Radius des Zylinders gegeben hast: Achte darauf, dass das Volumen und der Radius in den gleichen Einheiten angegeben sind (z.B. cm³ und cm). Quadriere den Radius. Dividiere das Volumen durch den Radius zum Quadrat und Pi, um die Höhe in der gleichen Einheit wie den Radius zu erhalten. Wenn du den Flächeninhalt und den Radius (r) gegeben hast: Vergewissere dich, dass die Fläche und der Radius die gleiche Einheit haben. Ziehe 2πr² von der Fläche ab. Dividiere das Ergebnis aus Schritt 2 durch 2πr. Das Ergebnis ist die Höhe des Zylinders.

Q: Wie kann ich den Radius eines Zylinders bestimmen?

Wenn du das Volumen und die Höhe des Zylinders gegeben hast: Achte darauf, dass das Volumen und die Höhe in den gleichen Einheiten angegeben sind (z.B. cm³ und cm). Dividiere das Volumen durch Pi und die Höhe. Ziehe die Quadratwurzel aus dem Ergebnis. Wenn du die Fläche und Höhe (h) gegeben hast: Setze die Höhe h und den Flächeninhalt in die Gleichung ein: Flächeninhalt = 2πrh + 2πr². Dividiere beide Seiten durch 2π. Subtrahiere Fläche/2π von beiden Seiten. Löse die resultierende quadratische Gleichung. Die positive Wurzel ist der Radius.

Q: Wie kannst du das Volumen eines ovalen Zylinders bestimmen?

Für die Volumenberechnung eines ovalen Zylinders: Multipliziere den kleinsten Radius des Ovales (Nebenachse) mit seinem größten Radius (Hauptachse). Multipliziere diese neue Zahl mit Pi . Dividiere das Ergebnis aus Schritt 2 durch 4. Das Ergebnis ist die Fläche des Ovales. Multipliziere die Fläche des Ovales mit der Höhe des Zylinders. Das Ergebnis ist das Volumen eines ovalen Zylinders.

Erstellt von Hanna Pamuła, Doktorand*in

Überprüft von Bogna Szyk und Jack Bowater

Übersetzt von Luise Schwenke

Luise Schwenke

Luise works as a German translator and Calculatorian at Omni. She holds a degree in Food Engineering from the University of Sciences - Neubrandenburg, Germany, and specialized her career in biotechnology. She worked in human genetic diagnostics, developing and producing pharmaceutical products for clinical phase 2 and 3 studies. She is always hungry for new fields to learn about that allow her to combine her creative and analytical thinking. Currently, she is getting her hands on coding, focusing on data science and big data. Luise spent an academic year in Brazil and loves traveling the world to experience and learn from different cultures. See full profile

Check our editorial policy

und Julia Kopczyńska, promovierend

Julia Kopczyńska

PhD candidate, Polish Academy of Sciences

LinkedInResearch Gate

A microbiologist with a low-key addiction to coffee. Since her Bachelor’s, she has focused on the gut microbiome and its role in human health. Now she hopes to find the golden bacteria to improve gut health in her Ph.D. project. She enjoys scientific writing and digging really deep into a topic. She has been living in 5 different countries and loves to travel to new places. In her free time, she likes to be active by playing volleyball, biking, and going for long walks. See full profile

Check our editorial policy

Neu

Inhalt

Wie wird das Zylinder-Volumen berechnet? – Formeln des Zylinder-Volumen-Rechners Volumen eines Hohlzylinders mit dem Zylindervolumen-Rechner ermitteln Volumen eines schrägen Zylinders FAQs

Unser Zylinder-Volumen-Rechner ermöglicht es dir, das Zylinder-Volumen zu berechnen. Egal, ob du herausfinden möchtest, wie viel Wasser in eine Kanne oder wie viel Kaffee in deinen Lieblingsbecher passt oder du das Volumen eines Trinkhalms bestimmen möchtest – der Zylindervolumen-Rechner ist hier um dir zu helfen. Du kannst mit diesem Rechner auch das Volumen eines Hohlzylinders bestimmen.

Wie wird das Zylinder-Volumen berechnet? – Formeln des Zylinder-Volumen-Rechners

Fangen wir ganz von vorne an – was ist ein Zylinder? Er ist ein Festkörper, der aus einer zylindrischen Oberfläche und zwei parallelen Ebenen besteht. Wir können ihn uns wie eine Dose vorstellen, die oben und unten einen Deckel hat. Wir berechnen das Zylinder-Volumen mit dem Durchmesser (oder Radius) und der Höhe. Schaue dir dir Formel zur Berechnung des Volumens eines Zylinders an:

Zylindervolumen = π × Zylinderradius² × Zylinderhöhe

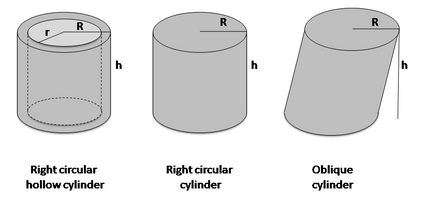
Der Zylinder-Volumen-Rechner hilft dir dabei, das Volumen von senkrechten, hohlen und schrägen Zylindern zu bestimmen:

Bilder von rechtwinkligen Hohlzylindern, rechtwinkligen Kreiszylindern und schrägen Zylindern.

Volumen eines Hohlzylinders mit dem Zylindervolumen-Rechner ermitteln

Der Hohlzylinder ist ein dreidimensionaler Bereich, der von zwei rechtwinkligen Kreiszylindern mit der gleichen Achse und zwei parallelen ringförmigen Basen senkrecht zur gemeinsamen Achse der Zylinder begrenzt wird.

Es ist einfacher, diese Definition zu verstehen, wenn du dir z. B. einen Trinkhalm oder ein Rohr vorstellst – der Hohlzylinder ist der Kunststoff, das Metall oder ein anderes Material. Die Formel für das Volumen eines Hohlzylinders lautet:

Zylindervolumen = π × (R² - r²) × Zylinderhöhe,

wobei R der Außenradius und r der Innenradius ist.

Du kannst das Volumen des Zylinders mit dem Durchmesser berechnen, wenn du den Außendurchmesser (D) und den Innendurchmesser (d) gegeben hast:

Zylindervolumen = π × [(D² - d²)/4] × Zylinderhöhe.

Um das Volumen eines Hohlzylinders zu berechnen, nehmen wir ein Beispiel aus dem wirklichen Leben, vielleicht... eine Rolle Toilettenpapier, warum nicht? 😀

Gib den Außendurchmesser des Zylinders in den Zylinder-Volumen-Rechner ein. Der Standard entspricht etwa 11 cm.
Bestimme den Innendurchmesser des Zylinders. Das ist der Innendurchmesser des Pappteils, etwa 4 cm.
Finde heraus, wie hoch der Zylinder ist; in unserem Fall sind es 9 cm.
Tadaaa! der Zylindervolumen-Rechner zeigt dir das Volumen des Hohlzylinders als 742,2 cm³ an.

Denk daran, dass das Ergebnis das Volumen des Papiers und der Pappe ist. Wenn du berechnen möchtest, wie viel Knete du in die Papprolle stecken kannst, verwende die Standardformel für die Berechnung des Volumens eines Zylinders – der Rechner wird es im Handumdrehen berechnen!

Volumen eines schrägen Zylinders

Der schräge Zylinder ist ein Zylinder, der sich „nach vorne neigt” – die Seiten stehen im Gegensatz zu einem normalen „senkrechten Zylinder” nicht senkrecht auf der Grundfläche. Wie berechnet man das Volumen eines schrägen Zylinders? Die Formel ist dieselbe wie für die Volumenberechnung eines senkrechten Zylinders. Denke nur daran, dass die Höhe senkrecht zu den Grundflächen sein muss.

Da du nun weißt, wie du das Volumen eines Zylinders mit dem Zylinder-Volumen-Rechner berechnen kannst, möchtest du vielleicht auch das Volumen anderer 3D-Körper bestimmen? Verwende diesen allgemeinen Volumenrechner!

Wenn du wissen möchtest, wie viele Teelöffel oder Tassen in deinen Behälter passen, verwende unseren Volumenumrechner 🇺🇸.

Um das Volumen der Pflanzenerde zu berechnen, das für Blumentöpfe verschiedener Formen benötigt wird – auch für den zylindrischen –, verwende den Blumenerde Rechner.

FAQs

Wo gibt es Zylinder in der Natur?

Zylinder sind überall um uns herum, und wir reden nicht nur von Pringles-Dosen. Obwohl die Dinge in der Natur selten perfekte Zylinder sind, sind einige Beispiele dafür Baumstämme und Pflanzenstämme, einige Knochen (und damit Körper) und die Geißeln von mikroskopischen Organismen. Diese machen einen großen Teil der natürlichen Objekte auf der Erde aus!

Wie zeichnet man einen Zylinder?

Um einen Zylinder zu zeichnen, befolge diese Schritte:

Zeichne einen leicht abgeflachten Kreis (Oval). Je flacher er ist, desto eher siehst du den Zylinder von der Seite an.
Zeichne zwei gleiche, parallele Linien von den äußeren Seiten deines Kreises nach unten.
Verbinde die Enden der beiden Linien mit einer halbkreisförmigen Linie, die genauso aussieht wie die untere Hälfte deines oberen Kreises.
Füge nach Bedarf Schatten und Schattierungen hinzu.

Wie berechnet man das Gewicht eines Zylinders?

So berechnest du das Gewicht eines Zylinders:

Quadriere den Radius des Zylinders.
Multipliziere das Quadrat des Radius mit Pi und der Zylinderhöhe.
Multipliziere das Volumen mit der Dichte des Zylinders. Das Ergebnis ist das Gewicht des Zylinders.

Wie berechnest du das Verhältnis von Oberfläche zu Volumen eines Zylinders?

Finde das Volumen des Zylinders mithilfe der Formel πr²h.
Bestimme den Flächeninhalt des Zylinders mit der Formel 2πrh + 2πr².
Bilde ein Verhältnis aus den beiden Formeln, d.h. πr²h / 2πrh + 2πr².
Alternativ kannst du die Formel auch zu rh / 2(h+r) vereinfachen .
Dividiere beide Seiten durch eine der Seiten, um das Verhältnis in seiner einfachsten Form zu erhalten.

Wie kannst du die Höhe eines Zylinders bestimmen?

Wenn du das Volumen und den Radius des Zylinders gegeben hast:

Achte darauf, dass das Volumen und der Radius in den gleichen Einheiten angegeben sind (z.B. cm³ und cm).
Quadriere den Radius.
Dividiere das Volumen durch den Radius zum Quadrat und Pi, um die Höhe in der gleichen Einheit wie den Radius zu erhalten.

Wenn du den Flächeninhalt und den Radius (r) gegeben hast:

Vergewissere dich, dass die Fläche und der Radius die gleiche Einheit haben.
Ziehe 2πr² von der Fläche ab.
Dividiere das Ergebnis aus Schritt 2 durch 2πr.
Das Ergebnis ist die Höhe des Zylinders.

Wie kann ich den Radius eines Zylinders bestimmen?

Wenn du das Volumen und die Höhe des Zylinders gegeben hast:

Achte darauf, dass das Volumen und die Höhe in den gleichen Einheiten angegeben sind (z.B. cm³ und cm).
Dividiere das Volumen durch Pi und die Höhe.
Ziehe die Quadratwurzel aus dem Ergebnis.

Wenn du die Fläche und Höhe (h) gegeben hast:

Setze die Höhe h und den Flächeninhalt in die Gleichung ein: Flächeninhalt = 2πrh + 2πr².
Dividiere beide Seiten durch 2π.
Subtrahiere Fläche/2π von beiden Seiten.
Löse die resultierende quadratische Gleichung.
Die positive Wurzel ist der Radius.

Wie kannst du das Volumen eines ovalen Zylinders bestimmen?

Für die Volumenberechnung eines ovalen Zylinders:

Multipliziere den kleinsten Radius des Ovales (Nebenachse) mit seinem größten Radius (Hauptachse).
Multipliziere diese neue Zahl mit Pi.
Dividiere das Ergebnis aus Schritt 2 durch 4. Das Ergebnis ist die Fläche des Ovales.
Multipliziere die Fläche des Ovales mit der Höhe des Zylinders.
Das Ergebnis ist das Volumen eines ovalen Zylinders.

Wie kannst du das Volumen eines schrägen Zylinders bestimmen?

Für die Volumenberechnung eines schrägen Zylinders:

Finde den Radius, die Seitenlänge und den Neigungswinkel des Zylinders.
Quadriere den Radius.
Multipliziere das Ergebnis mit Pi.
Nimm den Sinus des Winkels.
Multipliziere den Sinus mit der Seitenlänge.
Multipliziere das Ergebnis aus Schritt 3 und 5 miteinander.
Das Ergebnis ist das schräge Volumen.

Wie berechnest du den Hubraum eines Zylinders?

So berechnest du den Hubraum eines Zylinders:

Dividiere den Bohrungsdurchmesser durch 2, um den Bohrungsradius zu erhalten.
Quadriere den Bohrungsradius.
Multipliziere den quadratischen Radius mit Pi.
Multipliziere das Ergebnis aus Schritt 3 mit der Länge des Hubs. Achte darauf, dass die Einheiten für die Länge der Bohrung und des Hubs dieselben sind.
Das Ergebnis ist den Hubraum eines Zylinders.