Warteschlangentheorie Rechner

Im letzten Jahrhundert haben Mathematiker einen Rahmen entwickelt, der die Dynamik einer Warteschlange beschreibt: Lerne mit diesem Rechner die Grundlagen der Warteschlangentheorie.

Seitdem die Menschen in der Gesellschaft miteinander auskommen, haben sie auch angefangen zu warten. Sie warten darauf, dass sie an der Reihe sind, um zu reden, zu essen, Steuern zu zahlen und so weiter. Mit dem Wachstum der Bevölkerung und der zunehmenden Komplexität unseres täglichen Lebens warten wir auf immer mehr.

Da ist es nicht verwunderlich, dass sich jemand dafür interessiert, das Verhalten von Warteschlangen zu analysieren und zu modellieren. Zu wissen, wie lange es dauert, eine Warteschlange abzuarbeiten oder wie viele Kassen an einem anstrengenden Nachmittag geöffnet bleiben müssen, ist eine echte Hilfe, um viele zeitaufwändige Prozesse zu vereinfachen.

Jetzt kannst du dir vorstellen, warum die Warteschlangentheorie wichtig ist: Lies weiter, um mehr zu erfahren. In diesem Artikel erkundest du:

• Die Grundlagen der Warteschlangentheorie: Was ist die Warteschlangentheorie?
• Die wichtigsten Elemente einer Warteschlange und die Kendall-Notation;
• Der Grundstein der Warteschlangen: die $\textbf{\text{M}/\text{M}/1}$ Warteschlange;
• Das Hinzufügen von Bedienungen: die $\textbf{\text{M}/\text{M}/s}$ Warteschlange;
• Wie man unseren Warteschlangentheorie-Rechner benutzt, mit Beispielen; und
• Anwendungen der Warteschlangentheorie.

Dieser Artikel ist nur der Anfang der faszinierenden der Warteschlangentheorie. Wenn du interessiert bist, laden wir dich ein, von hier aus zu expandieren! Worauf wartest du? Wortspiel beabsichtigt. 😉

Du musst nicht wochenlang ein dickes Buch lesen, um zu verstehen, was die Warteschlangentheorie ist — auch wenn ihre mathematische Beschreibung ziemlich lang werden kann: Wir sprechen von dem gleichen Vorgang, sich in eine Warteschlange einzureihen — und zu warten — um Zugang zu einer Dienstleistung zu bekommen. Das tust du jedes Mal, wenn du Lebensmittel einkaufst oder zur Bank gehst.

Die Warteschlangentheorie wurde von Agner Krarup Erlang zu Anfang des 20. Jahrhunderts entwickelt, als er an der Analyse von Telefonnetzen arbeitete. Die Theorie entwickelte sich in den folgenden Jahren erfolgreich, dank der allgegenwärtigen Natur von Warteschlangen und der Nützlichkeit der Ergebnisse der Warteschlangenmodelle.

Was genau ist also die Warteschlangentheorie? Die Warteschlangentheorie analysiert das Verhalten einer Warteschlange, um Vorhersagen über ihre zukünftige Entwicklung zu treffen. Einige Beispiele dafür, was wir mit einem Warteschlangenmodell berechnen können, sind:

• Die Warte- und Servicezeit;
• Die Gesamtzahl der Kunden in der Warteschlange;
• Die Auslastung der Bedienung.

Und vieles mehr.

Die Warteschlangentheorie hat tiefe Wurzeln in der Statistik und Wahrscheinlichkeitstheorie. Das Eintreffen und die Bedienung von Kunden sind im Grunde stochastische Prozesse. Bei der Analyse solcher Prozesse über lange Zeiträume oder weit in der Zukunft verschwindet jedoch ihre implizite Zufälligkeit: Wir sprechen dann vom stetigen Zustand des Prozesses. Eine detaillierte Beschreibung der Grundlagen der Warteschlangentheorie erfordert ein gewisses statistisches Hintergrundwissen:

Wann nutzen wir die Warteschlangentheorie?

Die Warteschlangentheorie hat viele Anwendungsmöglichkeiten, z. B. bei der Verwaltung der Starts und Landungen auf Flughäfen, die Ausführung von Programmen auf deinem Computer und das Verhalten einer automatisierten Fabrik profitieren alle von einer sorgfältigen Analyse der Warteschlangen.

Von der Berechnung der Verkehrsdichte 🇺🇸 bis zur Graphentheorie – Warteschlangen sind überall, von der theoretischen Mathematik bis zu unserem täglichen Leben!

Apropos...

Im mathematischen Sinne ist eine Warteschlange ein komplexes Objekt, das durch eine Black Box modelliert wird. In dieser Black Box identifizieren wir zwei Ströme: einen eingehenden und einen ausgehenden. Was in der Box passiert, ist unbekannt, aber die ausgehenden Kunden sind glücklicher als die eingehenden.

Wenn wir einen Blick in die Box werfen, sehen wir eine bestimmte Anzahl an Bedienern, die die Anfragen der Kunden bearbeiten. Einige sind frei — sie warten darauf, einen Kunden zu empfangen, und andere sind gerade beschäftigt. So oder so, die Warteschlange bewegt sich weiter.

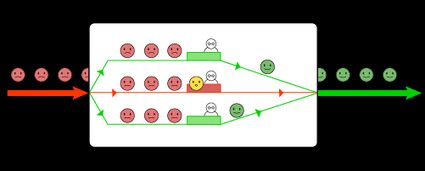
Normalerweise ist die Wartezeit der Kunden das wichtigste bei der Modellierung einer Warteschlange. Angenommen, du möchtest sie optimieren oder Fallstricke finden, die sie unnötig verlängern. Andere Ziele sind, die Auslastung der Bedienung zu optimieren oder die Länge der Warteschlange zu verringern.

Um eine Warteschlange im mathematischen Sinne zu beschreiben, muss man einige grundlegende Konzepte verstehen. Erstens wird eine Warteschlange durch Zustände dargestellt, von denen jeder die Anzahl der Personen in der Warteschlange angibt, die entweder warten oder bedient werden.

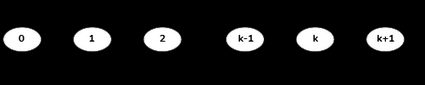
Mit einer gewissen Wahrscheinlichkeit — eine kurze Erinnerung daran, dass Warteschlangen in stochastischen Prozessen verwurzelt sind — kommen die Kunden an und erhalten die gewünschte Dienstleistung. Dadurch bewegt sich die Warteschlange: Ankünfte erhöhen den Zustand, und Dienstleistungen verringern ihn, um den Zustand $0$ zu erreichen.

Zustände sind mit Wahrscheinlichkeiten verbunden, aber die Warteschlangentheorie beschreibt eher die Zeit, die in einem bestimmten Zustand verbracht wird, als dass sie diese Menge definiert. Eine alternative Erklärung ist die Chance, eine bestimmte Anzahl von Kunden in der Warteschlange zu haben: Zeit und Besetzung sind überraschenderweise gleichwertig!

Die Reihenfolge, in der die Kunden in einer Warteschlange bedient werden, ist die Warteschlangen-Reihenfolge. Die gängigste Reihenfolge ist die „First in, first out“ -Reihenfolge (FIFO; wörtlich zuerst hinein – zuerst heraus), bei der die Priorität der Kunden von der Zeit in der Warteschlange abhängt.

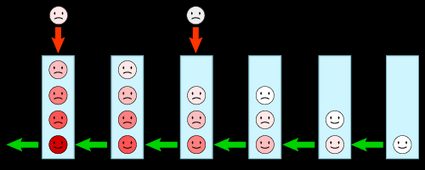
Andere Reihenfolgen sind:

• „Last in, first out“ (LIFO), bei der die zuletzt eingegebenen Gegenstände als erste bedient werden. Denk an einen Stapel Pfannkuchen oder Dinge, die in einen Rucksack gestopft werden. Diese Disziplin wird selten angewendet, wenn Menschen beteiligt sind: Wir lassen dich raten, warum!
• die Dringlichkeits-Reihenfolge kommt zum Einsatz, wenn die Reihenfolge der Bedienung von bestimmten Faktoren abhängt. In der Notaufnahme wird der Mann, dem ein Außerirdischer aus der Brust ragt, vor demjenigen behandelt, der sich den kleinen Finger an einer Ecke gestoßen hat: Du kannst sogar unseren Verletzungsschweregrad-Rechner 🇺🇸 benutzen, um die Priorität eines Patienten zu bestimmen.
• Rundum-Bedienung, bei der der Kunde für eine bestimmte Zeit bedient wird und sich dann wieder in die Warteschlange einreihen kann; und
• Bedienung in zufälliger Reihenfolge (SIRO), die niemandem gefällt.

Die meisten Modelle, und alle, die wir hier analysieren, verwenden die FIFO-Reihenfolge — sie ist am sinnvollsten!

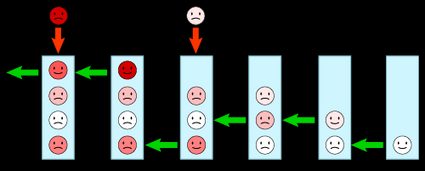
Erfahre mehr über die Arten von Warteschlangen in anderen Bereichen in Omni's FIFO Rechner 🇺🇸 und LIFO Rechner 🇺🇸!

Wie erkennen wir eine Warteschlange? David George Kendall beantwortete diese Frage, indem er eine einfache Notation aufstellte, die dabei hilft, schnell das richtige Set von Gleichungen für jede Situation zu wählen. Die grundlegende Kendall-Notation besteht aus drei Symbolen in der Form:

wobei:

• $a$ — Wahrscheinlichkeitsverteilung für die Intervalle zwischen den Kundenankünften;
• $b$ — Wahrscheinlichkeitsverteilung für die Bedienungszeit; und
• $c$ — Anzahl der Bedienungskräfte.

$a$ und $b$ können verschiedene Werte (Buchstaben) annehmen:

• $\text{M}$, steht für die Exponentialverteilung;
• $\text{E}$, steht für die Erlang-Verteilung; und
• $\text{G}$ für jede allgemeine Wahrscheinlichkeitsverteilung, deren Mittelwert und Varianz du kennst.

Du kannst die Kendall-Notation erweitern, um andere Parameter hinzuzufügen. Die Notation $a/b/c/d/e/f$ beinhaltet:

• $d$ — die maximale Anzahl von Kunden, die in der Warteschlange akzeptiert werden (denke an die Kapazität eines Büros);
• $e$ — die Größe der Kundenpopulation; und
• $f$ — die Warteschlangenreihenfolge.

Die am häufigsten analysierte Warteschlange ist die $\text{M}/\text{M}/1$ Warteschlange (Exponentialverteilung für die Intervalle zwischen den Ankünften und den Bearbeitungszeiten durch eine einzelne Bedienungskraft). Wir werden sie im Detail beschreiben. Andere häufig untersuchte Warteschlangen sind die $\text{M}/\text{M}/\text{s}$ und $\text{M}/\text{M}/\text{s}/\text{N}$.

Jetzt, wo du weißt, was die Warteschlangentheorie ist, können wir einige Modelle analysieren. Hier werden wir uns mit dem einfachsten Warteschlangenmodell beschäftigen. Nimm eine einzige Warteschlange mit einer einzigen Bedienungskraft und nimm an, dass:

• Die Zeitintervalle zwischen den Ankünften der aufeinanderfolgenden Kunden einer Exponentialverteilung folgen; und
• Die Bedienungszeiten einer Exponentialverteilung folgen.

Die Poisson-Verteilung und die Exponentialverteilung sind eng miteinander verbunden. Betrachten wir einen Poisson-Prozess (ein stochastischer Prozess, der das zufällige Auftreten eines Ereignisses beschreibt): Die Anzahl der Ereignisse in einer bestimmten Zeit folgt der Poisson-Verteilung. Das Intervall zwischen diesen Ereignissen hingegen folgt der Exponentialverteilung.

Im Zusammenhang mit einer $\text{M}/\text{M}/1$ Warteschlange bedeutet das, dass der Zeitpunkt der Ankunft jedes Kunden unabhängig von den anderen ist (keine Stoßzeiten oder Ausfallzeiten) und dass das Zeitintervall zwischen den Ankünften $t_{\mathrm{a}}$ dieser Verteilung folgt:

Die Bedienungskraft nimmt sich für jede Anfrage eine bestimmte Zeit, $t_{\mathrm{s}}$ die nicht von vorherigen oder zukünftigen Ereignissen abhängt (z. B. wird die Bedienung eines verspäteten Kunden nicht schneller gehen, weil die Pausenzeit naht!). Die Verteilung sieht folgendermaßen aus:

Ankunft und Bedienung ermöglichen es uns, die Warteschlange zwischen den Zuständen zu verschieben, auszugleichen oder zu überwiegen; sie lassen unser System tanzen.

Wenn wir uns im stetigen Zustand bewegen, können wir die beiden grundlegenden Mengen, die wir gerade kennengelernt haben, in den Formeln für die Verteilungen definieren:

• Die Ankunftsrate $\lambda$, die die Anzahl der Kunden beschreibt, die pro Zeiteinheit in die Warteschlange kommen; und
• Die Bedienungsrate $\mu$, die Anzahl der bedienten Kunden pro Zeiteinheit.

$\lambda$ und $\mu$ beschreiben, wie sich die Warteschlange zwischen den Zuständen bewegt, im Zusammenspiel mit dem Zeitanteil, der im Zustand $n$, $p_{n}$ verbracht wird (wobei $n$ die Anzahl der Kunden in der Warteschlange zu dieser Zeit angibt). Wir befolgen diese Regeln:

$\mu p_1$ steht für eine Warteschlange, in der ein Kunde bedient wird und die Warteschlange leer bleibt. Sie entspricht dem umgekehrten Prozess, bei dem ein Kunde eine leere Warteschlange betritt ($\lambda p_0$).

Für weitere Zustände, finden wir:

Wie berechent man diese Beziehungen? Mithilfe der zuvor gefundenen Äquivalenz und einer Analyse der Warteschlangendarstellung können wir die Summe der „Pfeile”, die von einem bestimmten Zustand aus ein- und ausgehen, gleichsetzen. Sieh dir das folgende Diagramm an:

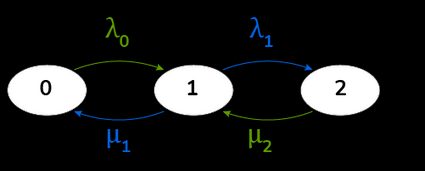
So bewegt sich die Warteschlange. Indem wir das Verhältnis zwischen der Ankunftsrate und der Bedienungsrate berechnen, finden wir die Bedienungsintensität $\rho$:

Analysieren wir nun die Leistungskennzahlen der Warteschlange. Wir beginnen mit der Durchschnittszahl der Kunden, $L$.

Mit dem Gesetz von Little können wir nun die Durchschnittszeit im System ableiten, $W$:

Die Zeit, die in der Warteschlange verbracht wird, ist von gleichem Interesse. Wir bezeichnen sie als $W_{\text{Q}}$ und berechnen sie erneut nach dem Gesetz von Little, diesmal aber ausgehend von der Anzahl der Kunden in der Warteschlange $L_{\text{Q}} = \rho L$:

Die vier Warteschlangengleichungen, die wir kennengelernt haben, definieren die grundlegenden Mengen in jedem Modell der Warteschlangentheorie.

Was kann bei der Analyse einer $\text{M}/\text{M}/1$ noch hilfreich sein? Wir können die Wahrscheinlichkeit, dass keine Kunden im System sind, $p_0$ definieren:

Wir berechnen die Wahrscheinlichkeit der Anwesenheit von $n$ Kunden in der Warteschlange, $p_{n}$ indem wir $\rho^n$ mal $p_0$ multiplizieren:

Wie sieht es mit den Werten von $p_n$ für alle anderen $n$ aus? Die Formel ist einfach und leitet sich aus mehreren Anwendungen des Übergangs zwischen den Zuständen der leeren Warteschlange ab:

Nachdem wir nun die $\text{M}/\text{M}/1$ Warteschlange analysiert haben, können wir zu etwas komplexeren Modellen übergehen.

Wir werden jetzt eine $\text{M}/\text{M}$ Warteschlange mit mehreren Bedienungskräften größer als einer analysieren. Hier müssen wir noch ein paar Mengen einführen.

$s$ ist die Anzahl der Bedienungskräfte im System. Jeder von ihnen bedient unabhängig voneinander und folgt der gleichen Exponentialverteilung und Service-Rate $\mu$.

Wir definieren die Auslastung der Bedienung $\rho$ als $\rho = \tfrac{\lambda}{s\mu}$ um. Du kannst dir $s\mu$ als die maximale Servicerate vorstellen. In der Tat ist eine $\text{M}/\text{M}/s$ Warteschlange nichts anderes als eine $\text{M}/\text{M}/1$ Warteschlange mit der Servicerate $s\mu$.

Führen wir noch eine letzte Menge ein, $\alpha = \tfrac{\lambda}{\mu}$ (die der Bedien ungsauslastung in der $\text{M}/\text{M}/1$ Warteschlange entspricht), also $\rho = \tfrac{\alpha}{s}$.

Achte auf das Verhalten im Serviceprozess. In der $\mathrm{M/M/s}$ Warteschlange können wir Situationen finden, in denen einige Servicekräfte einfach nur... abwarten, bis ein Kunde kommt. In dieser Situation ändern wir unsere Definition von $\mu$ leicht ab:

Die Wahrscheinlichkeit, dass sich in der Warteschlange keine Kunden befinden, hängt, wie du dir vorstellen kannst, von der Anzahl der Bedienungskräfte ab. Wir berechnen $p_0$ mit der Formel:

Die Anzahl der Kunden in der Warteschlange und im System, $L$ bzw. $L_{\text{q}}$, sind die Ergebnisse der $\text{M}/\text{M}/s$ Warteschlangengleichungen:

Lass uns die Wartezeiten berechnen. Wir machen es ähnlich wie bei der $\text{M}/\text{M}/1$ Warteschlange, aber wir müssen sie leicht abändern.

Die Wartezeit im System und in der Warteschlange sind:

Wir können eine letzte Menge einführen, die spezifisch für die $\text{M}/\text{M}/s$ Warteschlange ist: die Wahrscheinlichkeit, dass ein Kunde sich in die Warteschlange einreiht und keinen freie Bedienung findet. Wir nennen diese Menge Wahrscheinlichkeit der Kundenverzögerung, $C(s,\alpha)$:

$K$ ist ein Parameter, den wir schon kennen, wenn auch etwas anders:

Schließlich können wir die Wahrscheinlichkeit definieren, mit der sich die Warteschlange im Zustand $n$ befindet: Diese Menge haben wir bereits kennengelernt. Da das Verhalten dieser Warteschlange von der Anzahl der Kunden und der Bedienung abhängt:

Jetzt ist es an der Zeit, unseren Rechner für die Warteschlangentheorie kennenzulernen!

Mit unserem Rechner für die Warteschlangentheorie kannst du die Ergebnisse von $\text{M}/\text{M}/1$ Warteschlangen und $\text{M}/\text{M}/s$ Warteschlangen berechnen.

Der Rahmen der Warteschlangentheorie ist ziemlich komplex: Dieser kurze Artikel ist nur eine Einführung, und unser Rechner ist ziemlich grundlegend! Du kannst ihn erkunden, wenn du diesen spannenden Zweig der Mathematik gerade erst für dich entdeckt hast, oder ihn nutzen, um die Ergebnisse deiner Berechnungen zu überprüfen (insbesondere für Warteschlangen mit mehreren Bedienungen).

Wähle zunächst die Warteschlange aus, für die du dich interessierst. Gib die Werte ein, die du kennst; den Rest werden wir berechnen. Beachte, dass sich bestimmte Operationen nur schwer umkehren lassen: $p_0$ für eine $\mathrm{M/M/s}$ Warteschlange enthält eine Summation und eine Fakultät, und selbst bei aller Mühe könnten wir diesen Wert nicht als Eingabe verwenden. Er ist zusammen mit den anderen „schwierigen” Werten in unserem Rechner für die Warteschlangentheorie ausgegraut.