Geometrische Folge Rechner

Berechne mit diesem Rechner alles rund um die geometrische Folge. Er hilft dir, die Definition der geometrischen Folge zu verstehen und die Frage zu beantworten, eine geometrische Folge ist.
Wir erklären den Unterschied zwischen den beiden Gleichungen – explizite und rekursive Formel für eine geometrische Folge – und wie du die Formel für geometrische Folgen an einigen interessanten Beispielen anwenden kannst.

Der Rechner verfügt zudem über eine „geometrische Reihenrechner“ Funktion, welche die Summe einer geometrischen Folge berechnet. Sie geht von der expliziten Formel für eine geometrische Folge aus und berechnet daraus die Werte der geometrischen Reihe.

Eine geometrische Folge ist eine Folge von Zahlen, bei der alle Zahlen bis auf die erste durch Multiplikation der vorhergehenden Zahl mit einem festen Wert ungleich Null, dem Quotienten, berechnet werden. Wenn du noch nicht ganz verstehst, was eine geometrische Folge ist, sei nicht frustriert! Wir erklären dir, was das bedeutet und schauen uns die rekursive und explizite Formel für eine geometrische Folge an. Außerdem gehen wir ein paar Beispiele für geometrische Folgen durch.

Bevor wir uns die Definition im Detail ansehen, ist es wichtig, ein paar Dinge zu klären und so Verwirrung zu vermeiden. Zunächst einmal müssen wir verstehen, dass die geometrische Folge zwar durch die stetige Multiplikation von Zahlen mit einem Faktor entsteht, dies aber nichts mit der Fakultät zu tun hat (siehe unseren Fakultät Rechner 🇺🇸). Es gibt aber einen Zusammenhang mit dem größten gemeinsamen Teiler (ggT) und dem kleinsten gemeinsamen Vielfachen (kgV), da alle Zahlen einer geometrischen Folge einen ggT oder einen kgV haben, wenn die erste Zahl eine ganze Zahl ist.

Der ggT (siehe unseren ggT-Rechner) ist einfach die kleinste Zahl in der Folge. Umgekehrt ist das kgV einfach die größte der Zahlen in der Folge. In der Folge 3, 6, 12, 24, 48 ist der ggT zum Beispiel 3 und das kgV wäre gleich 48. Aber wenn wir nur die Zahlen 6, 12, 24 betrachten, wäre der ggT 6 und das kgV 24.

Schauen wir uns nun eine einfache Definition der geometrischen Folge an. Eine geometrische Folge ist eine Sammlung bestimmter Zahlen, die durch einen Quotienten miteinander in Verbindung stehen, den wir bereits erwähnt haben. Dieser Quotient gehört zusammen mit dem Anfangsterm einer geometrischen Folge zu ihren bestimmenden Merkmalen. Später werden wir sehen, wie diese beiden Zahlen die Grundlage der Definition einer geometrischen Folge bilden und wie sie bei der expliziten und rekursiven Formel für eine geometrische Folge verwendet werden.

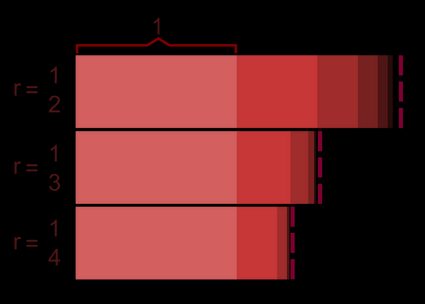
Konstruieren wir nun eine einfache geometrische Folge mit konkreten Werten für diese beiden definierenden Parameter. Der Einfachheit halber nehmen wir an, dass der erste Term $1$ und der Quotient $2$ ist. In diesem Fall wäre das erste Glied per Definition $a_1 = 1$, das zweite wäre $a_2 = a_1 \cdot 2 = 2$, das dritte Glied wäre dann $a_3 = a_2 × 2 = a_1 × 2^2 = 4$ usw. Das n-te Glied der Folge wäre somit:

wobei $n$ die Position des besagten Gliedes in der Folge ist.

Wie du siehst, ist der Quotient zweier beliebiger aufeinanderfolgender Glieder der Folge – wie auch in unserem Quotientenrechner 🇺🇸 definiert – konstant und gleich dem allgemeinen Quotienten der Folge.

Eine gängige Methode, eine geometrische Folge aufzuschreiben, ist, die ersten Terme explizit aufzuschreiben. So kannst du alle darauffolgende Zahlen der Folge berechnen; für unser Beispiel würden wir die Folge wie folgt aufschreiben:

Es gibt jedoch noch weitere, mathematische Wege, um die gleiche Information zu vermitteln. Diese anderen Wege sind die sogenannte explizite und rekursive Formel für geometrische Folgen. Jetzt, wo wir wissen, was eine geometrische Folge ist, können wir uns diese Formel genauer anschauen und herausfinden, wie wir dieselbe Information mit weniger Worten und mit größerer Präzision ausdrücken können.

Es gibt zwei verschiedene Möglichkeiten, eine geometrische Folge mit nur einer Formel mathematisch darzustellen: die explizite Formel für eine geometrische Folge und die rekursive Formel für eine geometrische Folge. Die erste davon haben wir bereits in unserem Beispiel für eine geometrische Folge angewendet. Es war eine konkrete, explizite Formel für dieses Beispiel. Damit die Formel für jede geometrische Folge gültig ist, musst du: den Anfangswert durch $a_1$ und den Quotienten durch $r$ ersetzen. Die allgemeine Formel für den n-ten Term lautet:

wobei $n \in \mathbb N$ bedeutet, dass $n = 1, 2, 3, ...$. Die explizite Formel für geometrische Folgen vermittelt die wichtigsten Informationen über eine geometrische Folge: den Anfangswert $a_1$, wie du einen beliebigen Wert aus dem ersten Wert berechnest und die Tatsache, dass es keinen Term vor dem Anfangsterm gibt.

Es gibt eine andere Möglichkeit, die gleichen Informationen mit einer anderen Art von Formel darzustellen: die rekursive Formel für eine geometrische Folge. Sie besteht aus zwei Teilen, die unterschiedliche Informationen aus der Definition der geometrischen Folge vermitteln. Der erste Teil erklärt, wie man mithilfe des Quotienten von einem beliebigen Glied der Folge zu einem beliebigen anderen Glied gelangt. Diese Bedeutung allein reicht nicht aus, um eine geometrische Folge von Grund auf zu konstruieren, da wir den Ausgangspunkt nicht kennen. Das ist der zweite Teil der Formel, der Anfangsterm (oder ein anderer, beliebiger Wert der Folge). Schauen wir uns an, wie diese rekursive Formel aussieht:

wobei $x$ verwendet wird, um auszudrücken, dass jede beliebige Zahl an dieser Stelle stehen kann, aber auch, dass es sich um eine konkrete Zahl handeln muss. Der Index $i$ steht für eine beliebige natürliche Zahl (genau wie $n$), wird aber anstelle von $n$ verwendet, um zu verdeutlichen, dass $i$ nicht dieselbe Zahl sein muss wie $n$.

Jetzt, wo du weißt, was eine geometrische Folge ist und wie man sie sowohl mittels der rekursiven als auch der expliziten Formel aufschreibt, ist es an der Zeit, dein Wissen anzuwenden und mit geometrischen Folgen zu rechnen! Mit unserem Tool kannst du alle Eigenschaften geometrischer Folgen berechnen, wie z.B. den Quotienten, den Anfangsterm, den n-ten Term usw.. Hier ist eine kurze Beschreibung, wie der Rechner aufgebaut ist:

1. Zuerst gibst du in den Rechner ein, was du über deine Folge weißt. Gib dafür den Wert für den Typ den du auswählst ein:
   • den gemeinsamen Quotienten und den ersten Term der Folge,
   • den gemeinsamen Quotienten und einen n-ten Term oder
   • zwei Terme.
2. Gib die Werte ein. Auf dieser Grundlage bestimmt der Rechner die gesamte geometrische Folge.
3. Standardmäßig zeigt der Rechner die ersten fünf Terme deiner Folge an. Du kannst die Anfangs- und Endterme nach deinen Bedürfnissen anpassen.

Unser Tool kann auch die Summe deiner Folge berechnen: für die gesamte Folge oder einen Teil davon. Im letzteren Fall reicht es aus, den Anfangs- und Endpunkt der Summe einzugeben, und schon zeigt dir der Rechner das Ergebnis an. Wie du in den folgenden Abschnitten lernen wirst, gibt es die unendliche Summe vielleicht gar nicht!

Bis jetzt haben wir über geometrische Folgen gesprochen, welche Sammlungen von Zahlen sind. Du kommst aber auch zu interessanten Ergebnissen, wenn du die Terme einer geometrischen Folge aufsummierst. Wenn es sich um eine endliche geometrische Folge mit einer begrenzten Anzahl von Termen handelt, ist das Verfahren einfach – du musst nur alle Elemente aufaddieren. Dies kannst du theoretisch sogar handschriftlich berechnen.

Aber wir können noch effizienter sein, indem wir die Formel für die geometrische Reihe verwenden und mit ihr herumprobieren. Dazu verwenden wir das mathematische Summenzeichen $\Sigma$, welches bedeutet, dass wir eine Sequenz von Termen aufsummieren. Wenn wir zum Beispiel eine geometrische Reihe mit dem Namen a_n haben und die Summe der geometrischen Reihe S nennen, würden sie in der folgenden Beziehung zueinander stehen:

wenn wir die ersten m Terme aufsummieren wollen, oder:

wenn wir alle Terme aufaddieren wollen.

Leider bleibt dann immer noch das Problem bestehen, den Wert der geometrischen Reihe tatsächlich zu berechnen. Du könntest zwar immer diesen Rechner zur Berechnung geometrischer Reihen verwenden, es ist aber natürlich viel hilfreicher, wenn du es auch handschriftlich schaffst. Es gibt einen Trick, der uns die Arbeit sehr erleichtern kann. Er besteht darin, die Gleichung der geometrischen Reihe wie folgt umzustellen und zu lösen:

Multipliziere nun beide Seiten mit $(1-r)$ und löse auf:

Dieses Ergebnis kannst du leicht selbst berechnen und es entspricht der Grundformel der geometrischen Reihe, wenn die Anzahl der Terme in der Reihe endlich ist. Da es sich hier aber um Mathematik und nicht um die Anwendungen im echten Leben handelt, können wir auch eine unendliche Anzahl von Termen in unserer geometrischen Reihe haben und trotzdem die Gesamtsumme aller Terme berechnen. Wie funktioniert diese Zauberei? – höre ich dich fragen. Keine Sorge, wir werden dir alle Details erklären, junger Lehrling.

Nachdem wir gesehen haben, wie man die Formel der geometrischen Reihe für eine endliche Anzahl von Termen herleitet, ist es selbstverständlich (zumindest für Mathematiker) sich zu fragen: Wie kann ich die unendliche Summe einer geometrischen Reihe berechnen? Es mag unmöglich erscheinen, aber mithilfe bestimmter Tricks können wir diesen Wert in ein paar einfachen Schritten berechnen. Dazu müssen wir das Konzept des Limes (oder Grenzwertes) einführen. Das ist ein mathematisches Verfahren, dank dessen wir verstehen können, was im Unendlichen passiert. Man kann damit auch versuchen, diejenigen Ausdrücke mathematisch zu definieren, die normalerweise undefiniert bleiben, wie z. B. Null geteilt durch Null oder Null hoch Null.

Über Grenzwerte zu sprechen ist ein sehr komplexes Thema, das den Rahmen dieses Rechners sprengen würde. Deshalb werden wir sie nur erwähnen und nicht ins Detail gehen. Mach dir aber keine Sorgen – wenn du wissen möchtest, wie Grenzwerte berechnet werden, gibt es zum Beispiel im Wikipedia-Artikel detaillierte Informationen zu diesem Thema.

Du kannst aber auch ohne tieferes Wissen über Grenzwerte die unendliche Summe einer geometrischen Reihe mit unserem Rechner bestimmen. Du musst nur beachten, dass nicht jede Reihe eine definierte Summe hat. Die Bedingungen, die eine Reihe erfüllen muss, damit ihre Summe eine Zahl ist (die Mathematiker nennen diese Konzept Konvergenz), sind im Prinzip ganz einfach. Wir erklären sie im folgenden Abschnitt.

Wenn es um mathematische Reihen (sowohl geometrische als auch arithmetische Reihen) geht, werden sie oft in zwei verschiedene Kategorien eingeteilt. Man unterscheidet, ob die Summe ihren unendlichen Elementen endlich (konvergente Reihen) oder unendlich/unbestimmt (divergente Reihen) ist. Der beste Weg, um herauszufinden, ob eine Reihe konvergent ist, ist durch die Berechnung der Summe ihrer unendlichen Anzahl von Elementen mithilfe des Limes. Abgesehen davon gibt es ein paar Tricks, mit denen wir schnell zwischen konvergenten und divergenten Reihen unterscheiden können, ohne alle Berechnungen durchführen zu müssen. Zu diesen Tricks gehören: sich den anfänglichen und den allgemeinen Term $a_n$ oder den Quotienten anzuschauen, oder sie mit anderen Reihen zu vergleichen.

Damit eine Reihe konvergent ist, muss der allgemeine Term $a_n$ bei jeder Erhöhung von $n$ kleiner werden. Wenn $a_n$ dabei kleiner wird, können wir nicht garantieren, dass die Reihe konvergent ist. Wenn $a_n$ bei der Erhöhung von $n$ konstant bleibt oder größer wird, können wir mit Sicherheit sagen, dass die Reihe divergent ist. Wenn wir uns nicht sicher sind, ob $a_n$ kleiner wird, können wir uns den Anfangswert und den Quotienten ansehen oder sogar einige der ersten Glieder berechnen. So bekommen wir ein Gefühl dafür, wie sich $a_n$ entwickelt.

Die zweite Möglichkeit ist der Vergleich der Entwicklung unserer geometrischen Reihe mit einer Reihe, von der wir sicher wissen, dass sie konvergiert (oder divergiert) ist. Das lässt sich mit einer schnellen Suche im Internet ganz einfach herausfinden. Ganz allgemein gesagt: Wenn die von uns untersuchte Reihe kleiner ist (d. h. $a_n$ ist kleiner) als eine Reihe, von der wir sicher wissen, dass sie konvergiert, können wir sicher sein, dass auch unsere Reihe konvergieren wird. Umgekehrt gilt: Wenn unsere Reihe größer ist als eine, von der wir sicher wissen, dass sie divergiert, wird sie immer divergieren. In den übrigen Fällen (größer als eine konvergente oder kleiner als eine divergente Reihe) können wir keine Aussage über unsere geometrische Reihe treffen und sind gezwungen, eine andere Reihe zum Vergleich zu finden oder eine andere Methode anzuwenden.

Diese Kriterien gelten für arithmetische und geometrische Folgen. Tatsächlich sind diese beiden eng miteinander verwandt und beide Folgen können durch das Potenzieren und den Logarithmus miteinander verbunden werden.

Wir haben bereits ein Beispiel für eine geometrische Folge in Form der Zweierpotenzfolge gesehen. Diese Folge ist für die binären Darstellung von Daten in Computern sehr wichtig. In dieser Folge finden wir Werte für die maximale zulässige Zahl in einem Computer (variiert je nach Art der Variablen, die wir verwenden), die Anzahl der Bytes in einem Gigabyte oder die Anzahl der Sekunden bis zum Ende der Unixzeit (sowohl den ursprünglichen als auch gepatchten Wert).

Zusätzlich zur Zweierpotenzfolge können wir jede andere Potenzfolge darstellen, wenn wir einfach $r = 2$ durch den Wert der Basis ersetzen, die uns interessiert. Potenzreihen sind weit verbreitet und können praktisch durch die geometrische Formel ausgedrückt werden. Es gibt aber auch wichtigere oder interessantere geometrische Reihen, wie z. B. die alternierende Reihe oder das verblüffende Zenons Paradoxon.

Beginnen wir mit den Zenons Paradoxien, insbesondere mit dem sogenannten Dichotomie-Paradoxon. Dieses Paradoxon ist im Grunde nur ein mathematisches Rätsel in Form einer unendlichen geometrischen Reihe. Zenon war ein griechischer Philosoph, der noch vor Sokrates lebte. Er erfand ein System, mit dem er beweisen konnte, dass Bewegung unmöglich ist und im wirklichen Leben niemals vorkommen darf. Die Idee ist, die Entfernung zwischen dem Startpunkt (A) und dem Zielpunkt (B) in zwei Hälften zu teilen. Wenn du die erste Hälfte zurückgelegt hast, teilst du die verbleibende Strecke noch einmal... Du kannst diesen Vorgang so oft wiederholen, wie du willst, sodass dir immer eine gewisse Strecke bis zum Punkt B bleibt.

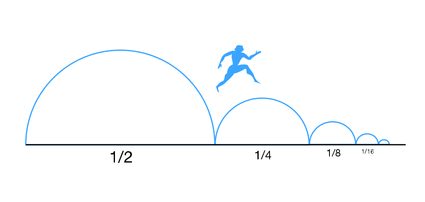
Zenons Paradoxon scheint vorauszusagen, dass wir, da wir eine unendliche Anzahl von Hälften laufen können, unendlich viel Zeit brauchen würden, um von A nach B zu kommen. Wie wir jedoch aus unserer alltäglichen Erfahrung wissen, ist das nicht wahr, und wir können immer in einer endlichen Zeit von Punkt A nach Punkt B gelangen (mit Ausnahme einiger Personen, die immer und überall unendlich spät anzukommen scheinen). Die Lösung für dieses scheinbare Paradoxon lässt sich mithilfe der Mathematik finden.

Wenn wir die Zeit (nennen wir sie erst einmal $t$), um von A nach B zu kommen, in Form einer geometrischen Reihe ausdrücken, hätten wir eine Reihe, die gegeben ist durch: $a_1 = t/2$ mit $r = 1/2$ als Quantil. Die erste Hälfte des Weges würde also $t/2$ dauern, dann würden wir die Hälfte der verbleibenden Strecke in $t/4$ zurücklegen, dann $t/8$ usw... Wenn wir nun die Summe der unendlichen geometrischen Reihe berechnen, würden wir feststellen, dass:

Das ist der mathematische Beweis dafür, dass wir in einer endlichen Zeit von A nach B kommen können (in diesem Fall in der Zeit $t$).

Zum Schluss, und falls Zenons Paradoxon eine noch keine genug verblüffende Erfahrung war, wollen wir die alternierende Reihe erwähnen.

Diese Reihe beginnt bei $a_1 = 1$ und hat den Quotienten $r = -1$, wir erhalten also:

Diese Reihe konvergiert nicht nach den Standardkriterien, weil das Ergebnis davon abhängt, ob wir eine gerade ($S = 0$) oder ungerade ($S = 1$) Anzahl von Termen nehmen. Es gibt jedoch einen Trick, mit dem wir diese Reihe zu einer endlichen Zahl konvergieren „lassen“ können. Der Trick selbst ist sehr einfach, beruht aber auf sehr komplexen mathematischen (und sogar meta-mathematischen) Argumenten. Wenn du ihn also jemals einem Mathematiker zeigst, riskierst du großen Ärger (eine ähnliche Reaktion kannst du erwarten, wenn du von der berüchtigten Collatz-Vermutung sprichst). Du wurdest gewarnt. Lass uns die „Lösung“ anschauen:

Wir multiplizieren beide Seiten mit $-1$:

Wenn wir jetzt nach $S$ auflösen:

Jetzt kannst du damit vor deinen Freunden angeben, solange sie keine Mathematiker sind.

Eine geometrische Folge ist eine Folge von Zahlen, bei der der nächste Term durch die Multiplikation des vorherigen Terms mit einer konstanten Zahl gebildet wird.

So findest du die Summe einer geometrischen Folge:

1. Berechne r (der Quotient) hoch n.
2. Subtrahiere das erhaltene rⁿ von 1.
3. Teile das Ergebnis durch (1 - r).
4. Multipliziere dieses Ergebnis mit dem ersten Term der Folge, a₁.

Um den n-ten Term einer geometrischen Folge zu finden:

1. Potenziere den Quotienten mit (n-1).
2. Multipliziere das Ergebnis mit dem ersten Term, a.

Um den Quotienten einer geometrischen Folge zu berechnen, teilst du zwei beliebige aufeinanderfolgende Terme der Folge.