Trigonometri – Kalkylator
Den här trigonometri kalkylatorn hjälper dig i två vanliga fall. Vill du räkna ut värdena för sin, cos, tan och deras omvända funktioner? Använd den första delen. Behöver du räkna ut en okänd vinkel eller sida i en rätvinklig triangel? Den andra delen är perfekt för det, fyll bara i 2–3 kända värden så får du snabbt ett exakt svar. Vill du lära dig mer om trigonometri och hur du använder den? Scrolla vidare!
För mer hjälp med trianglar – prova även vår sinusregel kalkylator 🇺🇸 och vår cosinusregel kalkylator 🇺🇸. De funkar för alla typer av trianglar.
Så använder du vår trigonometri kalkylator
Vår trigonometri kalkylator har två sektioner med olika funktioner. Här är en snabb guide så att du enkelt kan räkna ut det du behöver:
- I den första delen fyller du i en vinkel och får ut trigonometriska värden för sin, cos, tan och andra funktioner. Vill du använda en annan enhet? Klicka på enheten för att ändra den innan du skriver in vinkeln.
Till exempel, om du vill räkna ut sin(45°), skriver du bara in 45 grader – kalkylatorn visar direkt att sin(45°) = 0,70710678. Du får också automatiskt värden för cos(45°), tan(45°) och fler trigonometriska funktioner.
-
Den andra delen använder trigonometri för att räkna ut okända sidor eller vinklar i en rätvinklig triangel:
-
Börja med att välja vad du redan vet om triangeln. Du kan välja mellan "två sidor", "en vinkel och en sida" eller "area och en sida".
-
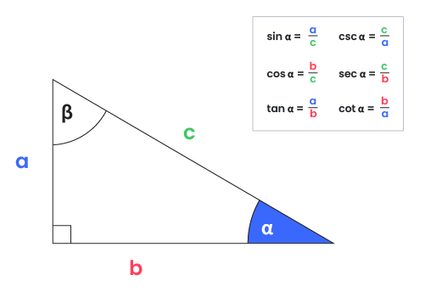
Titta på figuren längst ner i kalkylatorn för att förstå vad de olika parametrarna betyder. Fyll i det du vet. Vill du använda andra enheter? Ändra enheten innan du skriver in värdet.
-
Verktyget räknar sedan ut de saknade värdena med hjälp av trigonometri.
-
Om vi till exempel känner till två sidor, a = 7 cm och b = 12 cm, matar vi in dem i kalkylatorn. Genast ser vi att c = 13,892 cm, α = 30,256° och β = 59,74°.
Vi kan använda detta avsnitt i omvänd ordning också! Säg att vi vet att vinkeln β = 30°, b = 10 cm och c = 20 cm. Ange först β = 30°, och vi får genast veta att α = 60°. Skriv nu in b = 10 cm (se till att enheten är tum först). På samma sätt matar du in c = 20 cm, och vi ser att a = 17,32 cm.
Om du undrar hur trigonometri kan hjälpa dig att förstå så mycket om trianglar, fortsätt läsa den här artikeln. Den besvarar många av de vanligaste frågorna för dig som är ny till trigonometri.
Vad är trigonometri?
Trigonometri är en gren inom matematiken. Ordet kommer från grekiskan: trigōnon betyder "triangel" och metron betyder "mått". Som namnet antyder handlar trigonometri främst om vinklar och trianglar, särskilt om att definiera och använda förhållanden mellan sidor och vinklar i trianglar. Det används framför allt för att lösa trianglar, i synnerhet rätvinkliga trianglar, men även andra typer av trianglar.
🔎 Trigonometriska funktioner (sin, cos, tan) är alla förhållanden. Därför kan du räkna ut de saknade värdena med hjälp av vår förhållande kalkylator 🇺🇸!
Trigonometri har många användningsområden – från vardagliga problem som att räkna ut höjd eller avstånd mellan objekt, till satellitnavigering, astronomi och geografi. Dessutom är sinus- och cosinusfunktionerna grundläggande för att beskriva periodiska fenomen, tack vare dem kan vi beskriva svängningsrörelser (som i vår pendel kalkylator 🇺🇸) och vågor som ljud, vibrationer och ljus.
Många vetenskaps- och teknikområden använder trigonometri och trigonometriska funktioner – bland annat musik, akustik, elektronik, medicin och medicinsk bildbehandling, biologi, kemi, meteorologi, samt el-, maskin- och byggteknik. Även inom ekonomi förekommer det! Trigonometriska funktioner finns verkligen överallt omkring oss!
Trigonometri kalkylator som verktyg för att lösa rätvinkliga trianglar
För att hitta de okända sidorna eller vinklarna i en rätvinklig triangel behöver du bara fylla i de värden du känner till i trigonometri-kalkylatorn. Du behöver endast två givna värden i följande fall:
- en sida och en vinkel
- två sidor
- area och en sida
Kom ihåg att om du bara känner till två vinklar räcker det inte för att räkna ut sidorna i triangeln. Två trianglar med samma form (det vill säga lika vinklar) kan ändå ha olika storlek, det kallas för triangellikhet. Om sidorna också har samma längd är trianglarna kongruenta.
Möt skaparen bakom vår trigonometri kalkylator
Hej! Jag heter Hanna och ligger bakom den här trigonometri-kalkylatorn. Jag är doktor i maskinteknik och expert på att ta fram vetenskapliga verktyg. Jag insåg att en bra trigonometri-kalkylator skulle hjälpa mig att få rätt skärpedjup i fotograferingen, så jag satte mig ner och byggde en. Tack vare det har jag lyckats fånga några riktigt skarpa bilder på färgglada fåglar i naturen!
Vi lägger stor vikt vid att våra kalkylatorer ska vara så korrekta och pålitliga som möjligt. Varje verktyg granskas av en expert. Vill du veta mer om våra kvalitetskrav? Läs gärna vår sida om .
Vanliga frågor
Vad är trigonometri?
Trigonometri är läran om förhållandena i en triangel. I rätvinkliga trianglar är förhållandet mellan två sidor alltid detsamma och beskrivs med trigonometriska kvoter: cos, sin och tan. Trigonometri kan också användas för att räkna ut saknade värden i en triangel, till exempel med sinusregeln.
Hur gör man trigonometri?
- Identifiera vilka två värden du har: hypotenusan, närliggande sida, motstående sida eller en vinkel.
- Bestäm vilket värde du vill räkna ut.
- 'Välj rätt trigonometrisk formel (kom ihåg SOHCAHTOA).
- Fyll i dina kända värden i formeln.
- Lös ut det okända värdet.
- Dubbelkolla ditt svar med vår trigonometri kalkylator.
Är trigonometri svårt?
Trigonometri kan kännas svårt i början, men med lite övning kommer du att bemästra det! Här är några tips som hjälper:
- Märk ut hypotenusan, den närliggande och den motstående sidan i triangeln – det gör det lättare att veta vilken regel du ska använda.
- Kom ihåg minnesregeln SOHCAHTOA för trigonometriska samband!
Vad används trigonometri till?
Trigonometri används för att räkna ut information om alla typer av trianglar, särskilt rätvinkliga. Eftersom trianglar finns överallt i naturen, används trigonometri även utanför matematiken – till exempel inom byggteknik, fysik, kemiteknik och astronomi.
Vem uppfann trigonometri?
Eftersom trigonometri beskriver sambandet mellan vinklar och sidor i en triangel, är det inget som någon har uppfunnit utan det hade funnits där ändå! De första som började upptäcka trigonometri var forntida egyptier och babylonier, men det var Euklides och Arkimedes som först bevisade sambanden, även om de använde geometriska figurer istället för algebra.
När lär man sig trigonometri i skolan?
I Sverige brukar man först stöta på grunderna i trigonometri i årskurs 9 på högstadiet, och sedan fördjupas det i gymnasiet, särskilt i kurserna Matematik 1c och 2c.
Hur omvandlar man ett decimaltal till grader i trigonometri?
- Identifiera vilken trigonometrisk funktion du använder – tänk SOHCAHTOA.
- Använd inversen av funktionen, t.ex. sin⁻¹(0,5).
- Resultatet är vinkeln i grader.
- Dubbelkolla gärna svaret med vår trigonometri kalkylator.
Hur hittar man höjden på en triangel med hjälp av trigonometri?
- Rita triangeln och markera höjden. Dela triangeln i två rätvinkliga trianglar om det behövs.
- Lös någon av de nya trianglarna med vanlig trigonometri för att hitta höjden. Den motstående eller närliggande sidan blir nu hypotenusan.
- Kontrollera dina svar med kalkylatorn.
