Räkna ut hypotenusan
Med den här hypotenusa kalkylatorn kan du snabbt räkna ut den längsta sidan i en rätvinklig triangel. Om du undrar hur man hittar hypotenusan eller vill förstå formeln bakom Pythagoras sats, hittar du svaren här – tillsammans med ett enkelt exempel som visar hur du gör. Du får även se formeln för hypotenusan och hur vår kalkylator använder den för att ge dig ett exakt resultat.
Slösa inte mer tid, prova vår kalkylator för att räkna ut hypotenusa direkt!
Så använder du vår hypotenusa kalkylator
Så här gör du för att enkelt räkna ut hypotenusan i en rätvinklig triangel med hjälp av kalkylatorn:
-
Välj vilka värden du redan känner till. Du kan välja mellan:
-
Två sidor.
-
En vinkel och en sida.
-
Arean och en sida.
-
-
Fyll i de kända värdena, enligt markeringarna i diagrammet. Vill du ändra enhet? Klicka på den befintliga enheten, välj ny och skriv in ditt värde.
-
Verktyget räknar ut hypotenusan (och andra okända sidor eller vinklar). Du kan även ändra resultatets enhet om du vill.
Exempel: Tänk dig en rätvinklig triangel där vinkeln α = 60° och sidan a = 5 cm. Välj alternativet vinkel och en sida och fyll i dessa värden. Kalkylatorn visar direkt att:
- Sidan b = 2,887 cm;
- Vinkel β = 30°;
- Hypotenusa c = 5,774 cm.
Kalkylatorn fungerar även omvänt. Om du till exempel känner till hypotenusan (13 cm) och en annan sida (12 cm), välj alternativet två sidor och skriv in dessa värden. Resultatet? Sida b = 5 cm.
Läs vidare nedan för att förstå vad hypotenusan är och hur du beräknar den med olika metoder, med hjälp av Pythagoras sats, vinklar eller area.
Vad är hypotenusan i en triangel?
En hypotenusa är den längsta sidan i en rätvinklig triangel. Det är sidan som ligger mittemot den räta vinkeln (90°). Hypotenusans längd kan till exempel beräknas med hjälp av Pythagoras sats. Du kan läsa mer om detta i vår pythagoras sats kalkylator 🇺🇸.
Formeln för hypotenusan i en triangel
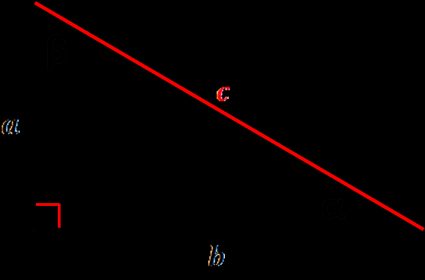
Denna kalkylator för hypotenusan har flera inbyggda formler, på så sätt ser vi till att den passar olika situationer du kan stöta på. Du kan räkna ut hypotenusan:
- Om du känner till de två kateterna i en rätvinklig triangel
Använd Pythagoras sats för att räkna ut hypotenusan utifrån de två benen i en rätvinklig triangel. Ta kvadratroten 🇺🇸 av summan av kvadraterna av sidorna:
c = √(a² + b²)

- Om du känner till en vinkel och en katet
c = a / sin(α) = b / sin(β), som vi förklarar i vår sinusregel kalkylator 🇺🇸.
- Om du känner till arean och en katet
Eftersom arean av en rätvinklig triangel är a × b / 2, så får vi:
c = √(a² + b²) = √(a² + (area × 2 / a)²) = √((area × 2 / b)² + b²).
Vill du lära dig mer om beräkningar med rätvinkliga trianglar? Kolla in vår area av en rätvinklig triangel kalkylator 🇺🇸 och kalkylatorn för sidor och vinklar i en rätvinklig triangel.
Exempel med stege – så hittar du hypotenusan i en rätvinklig triangel med denna hypotenusakalkylator

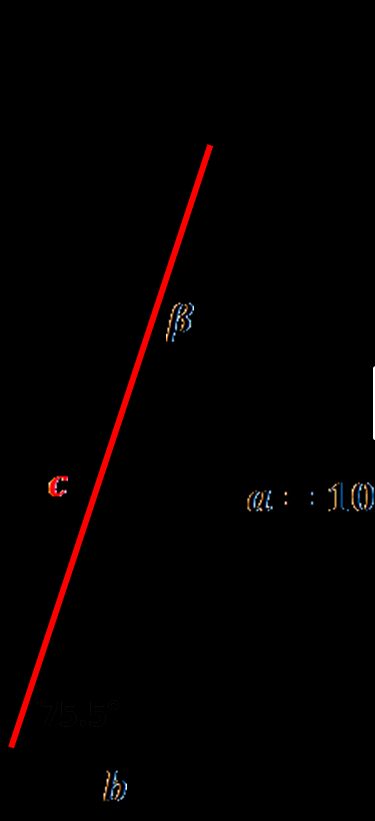
Låt oss räkna ut hur lång stegen behöver vara om vi ska rädda en kattunge från ett tak som är 10 meter högt. Kalkylatorn hjälper dig att ta reda på hur lång stegen behöver vara från marken upp till takets kant, men glöm inte att stegen även bör sticka ut lite över kanten!
- Välj det alternativ som passar dina beräkningar. Vi vet att taket är 10 meter högt och att den säkraste vinkeln för en stege är cirka 75,5°. I rullgardinsmenyn för givna värden, välj alternativet: vinkel ∡ och en sida.
- Byt enhet till meter.
-
Fyll i de givna värdena. Vår sida a (höjd) är 10 m och vinkeln α mellan stegen och marken är 75,5°.
-
Stegens längd, alltså hypotenusan visas direkt! Den är 10,33 m.
Du får också veta att vinkeln β = 14,5° och att sida b = 2,586 m. Den andra sidan är viktig eftersom den visar hur långt från väggen (eller takkanten) stegen ska placeras. En bra tumregel att minnas är 4:1-regeln, för varje fyra meter i höjd bör stegens fot stå en meter från väggen.
Hur hypotenusakalkylatorn kom till
Jag heter Hanna och har länge skapat verktyg för Omni Calculator – allt från enkla vardagsräknare till avancerade vetenskapliga hjälpmedel. Idén till just den här kalkylatorn fick jag när jag behövde räkna ut hur lång stege som krävdes för att nå upp till mitt tak. Jag insåg hur ofta rätvinkliga trianglar dyker upp i vardagen och bestämde mig för att skapa ett verktyg som kunde hjälpa andra i liknande situationer.
På Omni strävar vi alltid efter att vårt innehåll ska vara så korrekt och tillförlitligt som möjligt. Varje verktyg granskas noga av en expert inom ämnet. Läs mer om våra kvalitetsprinciper på vår sida om .
Vanliga frågor
Så här hittar du hypotenusan med hjälp av sinus:
- Använd sinusfunktionen på vinkeln (inte den räta vinkeln).
- Dividera längden på motstående sida med resultatet från steg 1.
- Resultatet är hypotenusan.
Är hypotenusan alltid den längsta sidan?
Ja, hypotenusan är alltid den längsta sidan, men bara i rätvinkliga trianglar. I likbenta trianglar kallas de två lika långa sidorna för ben, och i en liksidig triangel kallas alla sidor helt enkelt för sidor.
Så här hittar du hypotenusa, närliggande och motstående sida i en rätvinklig triangel:
- Identifiera den längsta sidan, det är hypotenusan.
- Välj en av de spetsiga vinklarna (mindre än 90°).
- Närliggande sidan är den som tillsammans med hypotenusan bildar den valda vinkeln.
- Motstående sidan är den som ligger mittemot den valda vinkeln, alltså den som inte bildar vinkeln.
Så räknar du ut höjden till hypotenusan i en rätvinklig triangel:
- Rita höjden från den räta vinkeln vinkelrätt mot hypotenusan. Du har nu delat triangeln i två mindre trianglar, som båda är likformiga med den ursprungliga.
- Dividera längden på den kortaste sidan i huvudtriangeln med hypotenusans längd.
- Multiplicera resultatet med längden på den återstående sidan för att få höjden.
- Alternativt kan du använda trigonometriska metoder, eftersom de nya trianglarnas vinklar är samma som i originaltriangeln.
Vad ska jag göra om hypotenusan är den motstående sidan?
Om hypotenusan verkar vara den motstående sidan har du valt fel vinkel. Du kan inte använda trigonometriska formler med den räta vinkeln. Välj istället en av de andra vinklarna i triangeln, då är hypotenusan alltid den sida som ligger mittemot den räta vinkeln, medan den motstående sidan är den som inte ingår i vinkeln du valt.
Hur konstruerar jag en linje som är vinkelrät mot hypotenusan?
- Ta fram en passare, en linjal och en penna.
- Ställ in passaren på längden av hypotenusan (eller valfri konstant längd).
- Rita en cirkel med centrum i ena änden av hypotenusan.
- Rita en till cirkel med centrum i andra änden.
- Dra en linje genom skärningspunkterna mellan cirklarna – den är vinkelrät mot hypotenusan.
Hur räknar jag ut hypotenusan i en likbent rätvinklig triangel?
- Ta reda på längden på en av de två lika långa sidorna (de som inte är hypotenusan).
- Kvadrera längden på sidan.
- Multiplicera resultatet med 2.
- Ta kvadratroten av resultatet, det är hypotenusans längd.
Vad är hypotenus-vinkel-satsen?
Hypotenus-vinkel-satsen är ett sätt att avgöra om två rätvinkliga trianglar är kongruenta (alltså exakt lika). Satsen säger att om två rätvinkliga trianglar har samma hypotenusa och en likadan spetsig vinkel, så är trianglarna kongruenta.
Var kommer ordet hypotenusa ifrån?
Ordet hypotenusa kommer från forngrekiskans hypoteinousa, som betyder ”den som sträcker sig under (en rät vinkel)”. Det härstammar i sin tur från hypo- (”under”) och teinein (”att sträcka”). Ännu en sak vi kan tacka de gamla grekerna för!
Hur löser man en rätvinklig triangel om man bara har hypotenusan?
Du kan inte lösa en rätvinklig triangel om du bara känner till hypotenusan. De andra två sidorna och vinklarna är fortfarande okända, vilket innebär att det finns oändligt många möjliga trianglar med samma hypotenusa.
