Calculadora da Lei de Wien

Com a calculadora da lei de Wien da Omni, você pode facilmente estimar a temperatura de um objeto, baseado em seu comprimento de onda ou frequência de pico do espectro de emissão térmica. Leia sobre a lei de Deslocamento de Wien, aprenda a fórmula da lei de Wien e avalie você mesmo a temperatura da superfície do Sol, da lava ou de qualquer corpo quente!

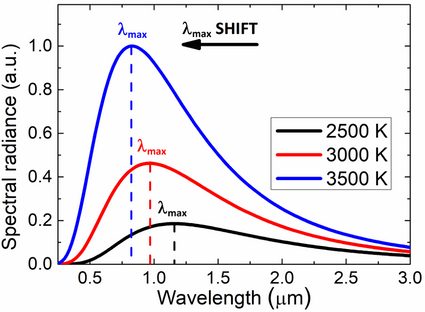
A lei de Deslocamento de Wien descreve uma das relações entre o espectro de emissão de um corpo negro e sua temperatura. Ela afirma que quanto maior a temperatura, menor o comprimento de onda λ_max para o qual a curva de radiação atinge seu máximo.

A mudança para comprimentos de onda mais curtos corresponde a fótons de energias mais altas. Em outras palavras, o λ_max (comprimento de onda máximo) é inversamente proporcional à temperatura.

A lei de Stefan-Boltzmann leva em conta a potência total irradiada de um corpo em qualquer temperatura (você pode verificá-la em nossa calculadora da lei de Stefan-Boltzmann 🇺🇸). Juntamente com a lei de Wien, elas se originam da distribuição de Planck.

A equação que descreve a lei de Wien é muito simples:

λ_max = b / T

onde:

• λ_max: pico do comprimento de onda da luz;
• T: temperatura absoluta de um corpo negro; e
• b = 2,8977719 mm·K: constante de deslocamento de Wien.

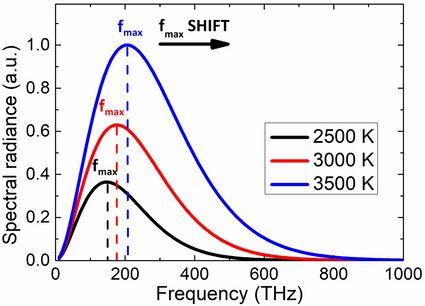
Embora a relação entre o comprimento de onda e a frequência das ondas eletromagnéticas seja relativamente simples (λ · f = c), não podemos calcular a frequência de pico f_max por meio dessa analogia. O motivo é que a radiância espectral é uma espécie de função de densidade de energia, portanto, sua forma e seu máximo dependem do argumento (comprimento de onda ou frequência, no nosso caso). Sabendo que a fórmula para a frequência de pico é:

f_max = k · T

onde k = 5,8789232 × 10¹⁰ Hz/K é uma constante numérica.

Não é possível derivar a fórmula da lei de Wien na física clássica. Várias observações que confirmam essa lei estão entre os experimentos (por exemplo, o efeito fotoelétrico), que contribuíram para a criação da mecânica quântica.

Você sabe como os cientistas podem encontrar a temperatura de objetos distantes? Normalmente, eles realizam uma observação espectroscópica, ajustam a função Planck à medição e obtêm um parâmetro que é a temperatura.

No entanto, também podemos obter uma boa estimativa aplicando a lei de Deslocamento de Wien aos resultados. Vamos tentar calcular a temperatura da superfície do Sol:

1. Encontre o comprimento de onda máximo de um espectro solar. É aproximadamente λ_max = 501,7 nm (ou 5,017 × 10-⁷ m na notação científica).

2. Transforme a fórmula da lei de Wien para obter a temperatura: T = b / λ_máx = 2,8977719 mm·K / 501,7 nm = 5.776 K.

Embora o corpo negro seja apenas um modelo idealizado, a lei de Wien é universal e pode ser uma aproximação muito precisa para objetos reais. Você também pode calcular a temperatura de qualquer corpo, como um metal quente ou lava, dependendo da cor da luz que ele emite. Use esta calculadora da lei de Wien e descubra se o resultado te surpreende ou não!