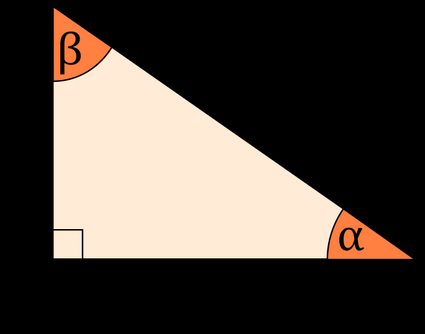
Zijden en hoeken van een rechthoekige driehoek berekenen

Het vinden van de ontbrekende zijde of hoek kan niet eenvoudiger zijn dan met onze geweldige tool - rechthoekige driehoek zijde en hoek calculator. Kies twee gegeven waarden, voer ze in de calculator in en de calculator bepaalt de resterende onbekende waarden in een oogwenk! Als je je afvraagt hoe je de ontbrekende zijde van een rechthoekige driehoek kunt vinden, scrol dan verder dan vind je de formules achter onze calculator.

Er zijn een paar methoden om de lengte van zijden van rechthoekige driehoeken te bepalen. Afhankelijk van wat er gegeven is, kun je verschillende relaties of wetten gebruiken om de ontbrekende zijde te vinden:

1. Aan de hand van twee zijden

Als je twee andere zijden van de rechthoekige driehoek kent, is dit de gemakkelijkste optie; je hoeft alleen maar de stelling van Pythagoras toe te passen:

a² + b² = c²

• Als zijde a de ontbrekende zijde is, transformeer de vergelijking dan naar de vorm waarbij a aan één zijde en bereken de vierkantswortel:

  a = √(c² - b²)

• Als zijde b onbekend is, dan:

  b = √(c² - a²)

• Als hypotenusa c ontbreekt, dan is de formule:

  c = √(a² + b²)

2. Aan de hand van een hoek en de schuine zijde

Pas de wet van sinus of goniometrie toe om de zijden van de rechthoekige driehoek te vinden:

• a = c × sin(α) of a = c × cos(β)

• b = c × sin(β) of b = c × cos(α)

3. Aan de hand van een hoek en een zijde

Vind de ontbrekende zijde met behulp van goniometrische functies:

• a = b × tan(α)

• b = a × tan(β)

4. Aan de hand van de oppervlakte en een zijde

Zoals we ons herinneren van basisformule oppervlakte driehoek 🇺🇸, kunnen we de oppervlakte berekenen door de hoogte en basis van de driehoek met elkaar te vermenigvuldigen en het resultaat door twee te delen. Een rechthoekige driehoek is een speciaal geval van een schalendriehoek, waarbij één zijde de hoogte is en de tweede zijde de basis, dus de vergelijking wordt vereenvoudigd tot:

oppervlakte = a × b / 2

Als we bijvoorbeeld alleen de oppervlakte van de rechthoekige driehoek en de lengte van de zijde a weten, kunnen we de vergelijking voor de andere zijden afleiden:

• b = 2 × oppervlakte / a
• c = √(a² + (2 × oppervlakte / a)²)

Als je één hoek kent behalve de rechte hoek, is de berekening van de derde hoek een fluitje van een cent:

Aan de hand van β: α = 90 - β

Aan de hand van α: β = 90 - α

Als echter slechts twee zijden van een driehoek gegeven zijn, moet je voor het vinden van de hoeken van een rechthoekige driehoek enkele goniometrische basisfuncties toepassen:

voor α:

• sin(α) = a / c dus α = arcsin(a / c) (inverse sinus);
• cos(α) = b / c dus α = arccos(b / c) (inverse cosinus);
• tan(α) = a / b dus α = arctan(a / b) (inverse tangens);
• cot(α) = b / a dus α = arccot(b / a) (inverse cotangens);

en voor β:

• sin(β) = b / c dus β = arcsin(b / c) (inverse sinus);
• cos(β) = a / c dus β = arccos(a / c) (inverse cosinus);
• tan(β) = b / a dus β = arctan(b / a) (inverse tangens);
• cot(β) = a / b dus β = arccot(a / b) (inverse cotangens).

Om een driehoek met één zijde op te lossen, heb je ook één van de niet-rechte hoeken nodig. Zo niet, dan is het onmogelijk:

1. Als je de hypotenusa hebt, vermenigvuldig die dan met sin(θ) om de lengte te krijgen van de zijde tegenover de hoek.

2. Je kunt ook de hypotenusa vermenigvuldigen met cos(θ) om de zijde te krijgen die aan de hoek grenst.

3. Als je de niet-hypotenusa zijde naast de hoek hebt, deel deze dan door cos(θ) om de lengte van de hypotenusa te krijgen.

4. Of vermenigvuldig deze lengte met tan(θ) om de lengte van de zijde tegenover de hoek te krijgen.

5. Als je een hoek hebt en de zijde ertegenover, dan kun je de lengte van de zijde delen door sin(θ) om de hypotenusa te krijgen.

6. Je kunt ook de lengte delen door tan(θ) om de lengte van de zijde naast de hoek te krijgen.

Laten we eens kijken hoe je de zijden van een rechthoekige driehoek kunt vinden met dit hulpmiddel:

1. Stel dat we de ontbrekende zijde willen vinden aan de hand van de oppervlakte en één zijde. Selecteer de juiste optie uit de lijst. Het is de derde.

2. Tik de gegeven waarden in. Bijvoorbeeld, de oppervlakte van een rechthoekige driehoek is gelijk aan 28 in² en b = 9 in.

3. Onze zijden en hoeken calculator voor rechthoekige driehoeken geeft ontbrekende zijden en hoeken weer! Nu weten we dat:

   • a = 6,222 in
   • c = 10,941 in
   • α = 34,66°
   • β = 55,34°

Laten we nu eens kijken hoe het vinden van de hoeken van een rechthoekige driehoek werkt:

1. Vernieuw de calculator. Kies de optie die je nodig hebt. Stel dat we twee zijden hebben en we willen alle hoeken vinden. De standaardoptie is de juiste.

2. Voer de lengtes van de zijden in. Onze rechthoekige driehoek heeft een schuine zijde gelijk aan 13 in en een zijde a = 5 in.

3. Ontbrekende zijde en hoeken worden weergegeven. In ons voorbeeld is b = 12 in, α = 22,62° en β = 67,38°.