Hypotenusa calculator
Met deze hypotenusa calculator bereken je snel de langste zijde van een rechthoekige driehoek. Als je wilt weten wat de hypotenusa van een rechthoekige driehoek is en hoe je die kunt bepalen, dan vind je hieronder de antwoorden, samen met een eenvoudig voorbeeld ter verduidelijking. We geven ook de formule voor de hypotenusa van een driehoek, zodat je de vergelijking achter onze calculator weet.
Wacht niet langer en probeer deze hypotenusa calculator!
Hoe kun je deze hypotenusa calculator gebruiken
De volgende instructies laten je zien hoe je deze calculator gemakkelijk kunt gebruiken:
-
Selecteer welke set parameters bekend is. Je kunt kiezen uit:
-
Twee zijden.
-
Een hoek en een zijde.
-
Een oppervlakte en een zijde.
-
-
Voer de bekende parameters in volgens de labels in het diagram. Om een parameter in een andere eenheid dan de standaardoptie in te voeren, klik je op de eenheid, wijzig je deze en voer je vervolgens de parameterwaarde in.
-
De tool zal onmiddellijk de hypotenusa berekenen (en eventuele andere ontbrekende afmetingen). Klik op de eenheid om deze te wijzigen in een eenheid naar keuze.
Stel je hebt een rechthoekige driehoek met hoek α = 60° en zijde a = 5 cm. We selecteren eerst de optie hoek en één zijde en voeren deze waarden in. De calculator berekent onmiddellijk dat:
- Zijde b = 2,887 cm;
- Hoek β = 30°; en
- Hypotenusa c = 5,774 cm.
De calculator kan ook andersom worden gebruikt. Stel dat je een onbekende zijde moet vinden met behulp van de hypotenusa (13 cm) en een bekende zijde (12 cm). Kies twee zijden als gegeven parameters en voer de hypotenusa c = 13 cm en zijde a = 12 cm in. Je kunt meteen zien dat zijde b = 5 cm.
In het volgende artikel wordt uitgelegd wat de hypotenusa is en hoe deze wordt berekend met behulp van verschillende parameters. Het is leuk en informatief, dus we raden je aan het te lezen om dit concept goed te kunnen begrijpen.
Wat is de hypotenusa van een driehoek?
Een hypotenusa is de langste zijde van een rechthoekige driehoek. Het is de zijde die tegenover de rechte hoek (90°) ligt. De lengte van de hypotenusa kan bijvoorbeeld worden gevonden met de stelling van Pythagoras. Je kunt hier meer over leren in onze stelling van Pythagoras calculator 🇺🇸.
Formule voor de hypotenusa van een driehoek
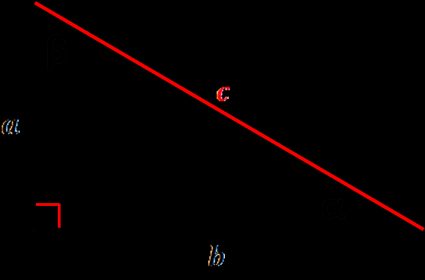
Deze hypotenusa calculator heeft een aantal formules geïmplementeerd - op deze manier hebben we ervoor gezorgd dat het past bij verschillende scenario's die je kunt tegenkomen. Je kunt de hypotenusa vinden:
- Aan de hand van de zijden van de rechthoekige driehoek
Gebruik de stelling van Pythagoras om de hypotenusa te berekenen aan de hand van de zijden van de rechthoekige driehoek. Neem een vierkantswortel 🇺🇸 van de som van hun kwadraten:
c = √(a² + b²)

- Aan de hand van een hoek en een zijde
c = a / sin(α) = b / sin(β), uitgelegd in onze wet van sinus calculator 🇺🇸.
- Aan de hand van de oppervlakte en een zijde
Omdat de oppervlakte van een rechthoekige driehoek gelijk is aan a × b / 2, dan is
c = √(a² + b²) = √(a² + (oppervlakte × 2 / a)²) = √((oppervlakte × 2 / b)² + b²).
Als je meer wilt weten over berekeningen met rechthoekige driehoeken, bekijk dan onze oppervlakte van een rechthoekige driehoek calculator 🇺🇸 en de rechthoekige driehoek zijde en hoek calculator.
Ladder voorbeeld - Hoe vind je de hypotenusa van een rechthoekige driehoek met deze hypotenusa calculator?

Laten we eens berekenen hoe lang de ladder moet zijn als we een kitten willen redden van een 305 cm hoog dak. De calculator helpt bij het vinden van de ladderlengte vanaf de grond tot aan de rand van het dak, maar vergeet niet het deel van de ladder dat over de rand moet uitsteken!
- Kies de optie die nodig is voor je berekeningen. We weten dat ons dak 305 cm hoog is en dat de veiligste hoek voor een ladder ~75,5° is. Selecteer de optie uit het keuzemenu van het gegeven vak: hoek ∡ en één zijde.
- Verander de eenheden in centimeter.
-
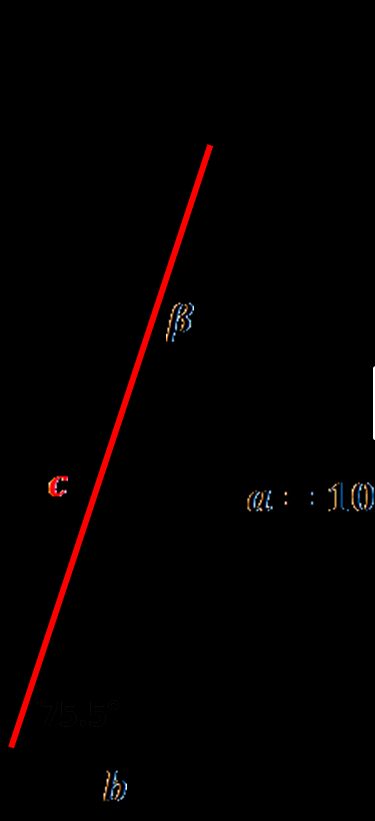
Voer de gegeven waarden in. Onze zijde a is 305 cm lang en de hoek α tussen de ladder en de grond is 75,5°.
-
De lengte van de ladder, onze schuine zijde van de rechte driehoek, verschijnt! Deze is gelijk aan 314,85 cm.
De hoek β = 14,5° en zijde b = 78,821 cm worden ook weergegeven. De tweede zijde is ook een belangrijke parameter, omdat het je vertelt hoe ver je de ladder van de muur (of liever van een dakrand) moet plaatsen. Het algemene principe dat je moet onthouden is de 4:1 regel - voor elke 120 cm verticale hoogte moet de laddervoet 30 cm van de muur af bewegen.
Het maken van de hypotenusa calculator
*Ik ben Hanna, al heel lang ontwerper bij Omni Calculator. Naast deze calculator heb ik al heel wat handige wetenschappelijke tools gemaakt die veel mensen elke dag weer helpen! Het idee voor deze calculator kwam bij me op toen ik de juiste lengte aan het berekenen was voor een ladder om op mijn dak te klimmen. Getroffen door de alomtegenwoordigheid van rechthoekige driehoeken in ons dagelijks leven, was ik vastbesloten om dit hulpmiddel te maken zodat het iedereen kan helpen!
Bij Omni besteden we uiterste zorg aan de kwaliteit van onze content, zodat deze zo nauwkeurig en betrouwbaar mogelijk is. Elke tool wordt beoordeeld door een getrainde expert en daarna nagelezen door iemand die de moedertaal spreekt. Je kunt meer te weten komen over onze normen op onze pagina.
Veelgestelde vragen
Hoe vind ik hypotenusa met sinus?
- Voer de sinus bewerking uit op de hoek (niet de rechte hoek).
- Deel de lengte van de zijde tegenover de hoek gebruikt in stap 1 door het resultaat van stap 1.
- Het resultaat is de hypotenusa.
Is de hypotenusa altijd de langste zijde?
Ja, de hypotenusa is altijd de langste zijde, maar alleen bij rechthoekige driehoeken. Bij gelijkbenige driehoeken worden de twee gelijke zijden de gelijkbenige zijden genoemd, terwijl bij een gelijkzijdige driehoek alle zijden gewoon zijden worden genoemd.
Hoe vind ik de aanliggende en overstaande zijde van de hypotenusa?
- Zoek de langste zijde en noem deze de hypotenusa.
- Je kunt de aanliggende en overstaande zijden alleen vinden als je één hoek kiest die kleiner is dan 90 graden.
- De aanliggende zijde is de zijde die samen met de hypotenusa de gekozen hoek vormt.
- De tegenovergestelde zijde is de zijde die niet de gekozen hoek vormt.
Hoe vind je de hoogte van een hypotenusa?
- Teken de hoogte van de hypotenusa op de driehoek. De twee nieuwe driehoeken die je hebt gemaakt lijken op elkaar en op de hoofddriehoek.
- Deel de lengte van de kortste zijde van de hoofddriehoek door de hypotenusa van de hoofddriehoek.
- Vermenigvuldig de uitkomst met de lengte van de overgebleven zijde om de lengte van de hoogte te krijgen.
- Als alternatief zullen de hoeken binnen de kleinere driehoeken hetzelfde zijn als de hoeken van de hoofddriehoek, dus je kunt goniometrie uitvoeren om het op een andere manier te vinden.
Wat moet ik doen als de hypotenusa de overstaande zijde is?
Als de hypotenusa de overstaande zijde is, dan bekijk je de verkeerde hoek - je kunt goniometrie niet gebruiken voor de rechte hoek van een driehoek. Bekijk een van de andere hoeken. Dit is de aanliggende hoek. De overstaande zijde is de zijde die die hoek niet vormt.
Hoe construeer ik een lijn loodrecht op de hypotenusa?
- Koop een passer, een liniaal en een pen of potlood.
- Stel je passer in op de lengte van de hypotenusa (of een willekeurige lengte, zolang deze maar constant blijft).
- Teken een cirkel met het middelpunt op een van de uiteinden van de hypotenusa.
- Teken nog een cirkel met het middelpunt aan het andere uiteinde van de hypotenusa.
- Teken een lijn tussen de twee punten waar deze cirkels elkaar raken. Deze lijn staat loodrecht op de hypotenusa.
Hoe vind ik de hypotenusa van een gelijkbenige rechthoekige driehoek?
- Bereken de lengte van een van de niet-hypotenusa zijden.
- Kwadrateer de lengte van de zijde.
- Verdubbel het resultaat van de vorige stap.
- Bereken de wortel van het resultaat van stap 3. Dit is de lengte van de hypotenusa.
Wat is de stelling van de hypotenusa-hoek?
Wat is de stelling van de hypotenusa-hoek is een manier om te testen of twee rechthoekige driehoeken al dan niet congruent zijn. Het stelt dat als twee rechthoekige driehoeken een schuine zijde en een scherpe hoek hebben die hetzelfde zijn, ze congruent zijn.
Waar komt het woord hypotenusa vandaan?
Het woord hypotenusa komt van het Oudgriekse hypoteinousa, wat 'uitrekken onder (een rechte hoek)' betekent. Dit komt weer van hypo- 'onder' en teinein 'uitrekken'. Nog iets waar we de Oude Grieken voor moeten bedanken!
Hoe los ik een rechthoekige driehoek op met alleen de hypotenusa?
Je kunt een rechthoekige driehoek niet oplossen met alleen de hypotenusa. Dit komt omdat de andere twee zijden en hoeken nog steeds ongedefinieerd zijn, dus de driehoek kan nog steeds vele vormen hebben.
