Combinatie berekenen

Deze combinatie calculator (n kies k calculator) is een hulpmiddel dat je niet alleen helpt bij het bepalen van het aantal combinaties in een verzameling (vaak aangeduid als nCr), maar je ook elke mogelijke combinatie (of permutatie) van je verzameling laat zien, tot de lengte van 10 elementen (of 300 combinaties/permutaties). Wees echter voorzichtig! Het eindresultaat kan erg lang zijn in onze combinatiegenerator. Als je je afvraagt hoeveel verschillende combinaties er mogelijk zijn van een specifiek aantal elementen en steekproefgrootte, probeer dan nu onze combinatie calculator!

Als je nog steeds niet zeker weet wat een combinatie is, dan wordt dat allemaal uitgelegd in het volgende artikel. Je vindt hier een combinatiedefinitie samen met de combinatieformule (met en zonder herhalingen). We laten je zien hoe je combinaties kunt berekenen en wat de lineaire combinatie en combinatiekans zijn. Tot slot zullen we het hebben over de relatie tussen permutatie en combinatie. Kort gezegd houdt permutatie rekening met de volgorde van de leden en combinatie niet. Hieronder vind je meer informatie!

Heb je je ooit afgevraagd wat je kansen zijn om de hoofdprijs in een loterij te winnen? Hoe waarschijnlijk is het winnen van de tweede prijs? Om beide en soortgelijke vragen te beantwoorden, moet je combinaties gebruiken. We hebben een speciaal hulpmiddel voor dat soort problemen. Onze loterij calculator 🇺🇸 schat niet alleen de combinatiekans om een loterijspel te winnen, maar geeft ook een loterijformule. Probeer het maar eens! Je zult ontdekken hoe groot (of klein) die getallen eigenlijk zijn.

De combinatiedefinitie zegt dat het gaat om het aantal manieren waarop je r elementen kunt kiezen uit een verzameling die n verschillende objecten bevat (daarom worden zulke problemen vaak "n kies r" problemen genoemd). De volgorde waarin je de elementen kiest is niet essentieel in tegenstelling tot de permutatie (je kunt een uitgebreide uitleg van dat probleem vinden in de permutatie en combinatie sectie).

Het zoeken naar elke combinatie van een verzameling objecten is een zuiver wiskundig probleem. Je hebt waarschijnlijk al geleerd hoe je bijvoorbeeld de grootste gemene deler (GGD) of het kleinste gemene veelvoud (KGV) kunt vinden. Nou, een combinatie is een heel ander verhaal. Laten we eens kijken hoe ingewikkeld het kan zijn.

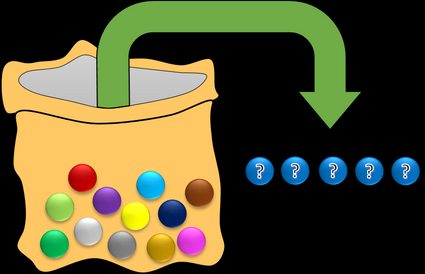
Stel je hebt een zak met twaalf ballen, die allemaal een andere kleur hebben. Je kiest willekeurig vijf ballen. Hoeveel verschillende verzamelingen ballen kun je krijgen? Of, met andere woorden, hoeveel verschillende combinaties kun je krijgen?

Wiskundigen geven de exacte oplossing voor veel verschillende problemen, bijvoorbeeld hoe je een vierkante meter berekent of hoe je het volume berekent. Is er een vergelijkbare benadering voor het schatten van het aantal combinaties in het bovenstaande voorbeeld met ballen?

Gelukkig hoef je niet alle mogelijke verzamelingen op te schrijven! Hoe bereken je dan de combinaties? Je kunt de volgende combinatieformule gebruiken waarmee je in een handomdraai het aantal combinaties kunt berekenen:

waarbij:

• $C(n,r)$ het aantal combinaties is;
• $n$ het totale aantal elementen in de verzameling is; en
• $r$ het aantal elementen is dat je kiest uit deze verzameling.

Het uitroepteken $!$ staat voor een factorial. Bekijk onze factorial calculator 🇺🇸 voor meer informatie over dit onderwerp. De uitdrukking aan de rechterkant wordt ook wel de binomiaalcoëfficiënt genoemd.

Laten we deze vergelijking toepassen op ons probleem met kleurrijke ballen. We moeten bepalen hoeveel verschillende combinaties er zijn:

Je zult merken dat, volgens de combinatieformule, het aantal combinaties voor het kiezen van slechts één element eenvoudig $n$ is. Aan de andere kant, als je alle elementen moet kiezen, is er maar één manier om dat te doen. Laten we deze combinatie-eigenschap eens controleren met ons voorbeeld. Je hebt het totale aantal objecten dat gelijk is aan $n = 12$. Elke letter die wordt weergegeven in de nCr calculator staat voor een bepaalde kleur van een bal, bijvoorbeeld A is rood, B is geel, C is groen, enzovoort. Als je slechts één element $r = 1$ kiest uit die verzameling, is het aantal combinaties $12$ - omdat er 12 verschillende ballen zijn. Als je echter $r = 12$ elementen kiest, zal er slechts $1$ mogelijke combinatie zijn die elke bal bevat. Probeer het zelf met de n kies r calculator!

Op dit punt weet je waarschijnlijk alles wat je moet weten over combinaties en de combinatieformule. Als je nog niet genoeg weet, vertellen we in de volgende paragrafen meer over de verschillen tussen permutatie en combinatie (die vaak onterecht als hetzelfde worden beschouwd), combinatiekans en lineaire combinatie.

Stel je voor dat je dezelfde zak met gekleurde ballen hebt als in het voorbeeld in de vorige paragraaf. Opnieuw kies je willekeurig vijf ballen, maar deze keer is de volgorde belangrijk - het maakt uit of je de rode bal als eerste of als derde kiest. Laten we een eenvoudiger voorbeeld nemen waarbij je drie ballen kiest met de namen R(rood), B(blauw), G(groen). Er zijn zes permutaties van deze verzameling (de volgorde van de letters bepaalt de volgorde van de gekozen ballen): RBG, RGB, BRG, BGR, GRB, GBR, en de combinatiedefinitie zegt dat er maar één combinatie is! Dit is het cruciale verschil.

Per definitie is een permutatie de herschikking van alle leden van een verzameling in een bepaalde volgorde. In de literatuur veralgemenen we dit concept echter vaak en stappen we af van de eis dat we alle elementen van een gegeven verzameling moeten gebruiken. Dat maakt permutatie en combinatie zo vergelijkbaar. Deze betekenis van permutatie bepaalt het aantal manieren waarop je r elementen kunt kiezen en rangschikken uit een verzameling die n verschillende objecten bevat. Dit wordt r-permutaties van n genoemd (soms variaties genoemd). Als je op zoek bent naar een nog diepgaandere uitleg, bekijk dan de permutatie calculator 🇺🇸 voor meer informatie.

De permutatieformule is zoals hieronder:

Lijkt deze vergelijking niet veel op de combinatieformule? In feite kun je, als je het aantal combinaties weet, gemakkelijk het aantal permutaties berekenen:

Met deze combinatie calculator kun je het aantal permutaties vinden door de bijbehorende optie in het selectievakje te selecteren.

Je vraagt je misschien af wanneer je een permutatie moet gebruiken in plaats van een combinatie. Nou, dat hangt ervan af of je rekening moet houden met de volgorde of niet. Laten we bijvoorbeeld zeggen dat je een stapel van negen kaarten hebt met cijfers van 1 tot 9. Je trekt drie willekeurige kaarten en legt ze op een rij op tafel, zodat er een getal van drie cijfers ontstaat, bijvoorbeeld 425 of 837. Hoeveel verschillende getallen kun je maken?

Controleer het resultaat met onze nCr-calculator! En hoeveel verschillende combinaties zijn er?

Het aantal combinaties is altijd kleiner dan het aantal permutaties. Deze keer is het zes keer kleiner (als je 84 vermenigvuldigt met $3! = 6$, krijg je 504). Het komt voort uit het feit dat elke drie kaarten die je kiest op zes verschillende manieren herschikt kunnen worden, net als in het vorige voorbeeld met drie gekleurde ballen.

Om onze overwegingen over permutatie en combinatie af te ronden, moeten we een soortgelijke selectie introduceren, maar deze keer met toegestane herhalingen. Dit betekent dat elke keer nadat je een element hebt gekozen uit de verzameling van n verschillende objecten, je het terugplaatst in die verzameling. In het voorbeeld met de gekleurde ballen, neem je één bal uit de zak, onthoud je welke je hebt getrokken en stop je die terug in de zak. Analoog daaraan kies je in het tweede voorbeeld met kaarten één kaart, noteert het nummer van die kaart en legt die terug in de stapel. Op die manier kun je bijvoorbeeld twee rode ballen in je combinatie hebben of 228 als permutatie.

Je raadt waarschijnlijk al dat beide formules veel ingewikkelder worden. Toch is het niet zo ingewikkeld als het berekenen van het alcoholpercentage van je zelfgebrouwen bier. In het geval van permutatie wordt de vergelijking zelfs nog eenvoudiger. De formule voor combinatie met herhaling is als volgt:

en voor permutatie met herhaling:

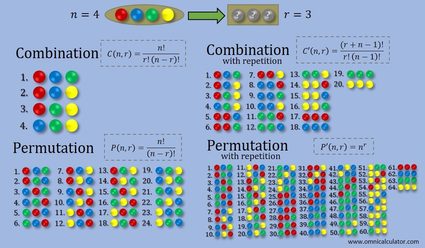
In de afbeelding hieronder geven we een overzicht van de verschillen tussen vier soorten selectie van een object: combinatie, combinatie met herhaling, permutatie en permutatie met herhaling. Het is een voorbeeld waarin je vier ballen van verschillende kleuren hebt, en je er drie kiest. In het geval van selecties met herhaling kun je een van de ballen meerdere keren kiezen. Als je het met permutaties wilt proberen, wees dan voorzichtig, er zullen duizenden verschillende verzamelingen zijn! Je kunt echter nog steeds veilig berekenen hoeveel het er zijn (permutaties zijn beschikbaar in onze tool).

Laten we beginnen met de combinatiekans, een essentieel element in veel statistische problemen. Een voorbeeld hierboven legt het gemakkelijk uit - je pakt drie van de vier gekleurde ballen uit de zak. Laten we zeggen dat je de kans (waarschijnlijkheid) wilt weten dat er een rode bal tussen zit. Er zijn vier verschillende combinaties en de rode bal zit in drie combinaties. De combinatiekans is dan:

Als je drie willekeurige ballen uit de zak trekt, kies je in 75% van de gevallen een rode bal. Om waarschijnlijkheid uit te drukken, gebruiken we meestal het procentteken.

Stel nu dat je één bal pakt, noteert welke kleur je hebt en hem terug in de zak stopt. Wat is de combinatiekans dat je minstens één rode bal krijgt? Dit is een 'combinatie met herhaling' probleem. In de afbeelding hierboven kun je zien dat er in totaal twintig combinaties zijn en dat de rode bal in tien daarvan voorkomt, dus:

Ben je hierdoor verrast? Nou, dat zou niet moeten. Als je de eerste bal teruglegt, bijvoorbeeld een blauwe bal, kun je deze ook als tweede en derde bal trekken. De kans dat je een rode bal krijgt wordt dus verlaagd. Je kunt analoge overwegingen maken met permutatie. Probeer een probleem op te lossen met de zak met gekleurde ballen: wat is de kans dat je eerst gekozen bal rood is?

Stel dat je ons niet vertrouwt en het zelf wilt testen. Je trekt drie van de vier ballen en controleert of er een rode bal bij zit of niet (zoals in het eerste voorbeeld van deze paragraaf). Je herhaalt dat proces nog drie keer, en je krijgt de rode bal slechts in één van de vier gevallen - $25\%$ van de gevallen. Je verwachtte $75\%$ volgens de theorie. Wat is er gebeurd? Nou, zo werkt waarschijnlijkheid! Er is de wet van de grote getallen die het resultaat beschrijft van een groot aantal keren hetzelfde experiment uitvoeren. Als je de trekking herhaalt, bijvoorbeeld honderd keer, kom je veel dichter bij $75\%$.

Bovendien leidt de wet van de grote getallen bijna altijd tot de standaard normale verdeling, die bijvoorbeeld intelligentie of de lengte van mensen kan beschrijven met een zogenaamde p-waarde. Wil je meer weten? Normale verdeling calculator 🇺🇸 is waar je moet wezen!

Heb je ooit gehoord van de lineaire combinatie? In feite heeft het, ondanks dat het woord combinatie erin voorkomt, niet veel gemeen met wat we tot nu toe hebben geleerd. Toch zullen we proberen het kort uit te leggen. Een lineaire combinatie is het resultaat van het nemen van een verzameling termen en het vermenigvuldigen van elke term met een constante en het optellen van de resultaten. Het wordt vaak gebruikt in de golffysica om de diffractieroostervergelijking te voorspellen of zelfs in de kwantumfysica vanwege de de Broglie-vergelijking. Hier zie je enkele veelvoorkomende voorbeelden van een lineaire combinatie:

1. Vectoren. Elke vector in 3D kan worden ontbonden in drie eenheidsvectoren $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ en $\^e_3 = (0,0,1)$. Bijvoorbeeld $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ en dat is lineaire combinatie.
2. Functies. Laten we zeggen dat je twee functies hebt $f(x) = \text{e}^x$ en $g(x) = \text{e}^{-x}$. Uit die twee functies kun je lineaire combinaties maken die de hyperbolische sinus $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ of cosinus $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$ beschrijven. Je kunt iets soortgelijks doen met de normale sinus en cosinus, maar dan moet je het imaginaire getal $i$ gebruiken. We vertellen hier meer over in het laatste deel van de vierkantswortel calculator 🇺🇸.
3. Polynomen. Je hebt bijvoorbeeld drie polynomen $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ en je wilt de functie $q(x) = 2x^2 + x + 3$ uitdrukken als een lineaire combinatie van die polynomen. Dat is niet altijd mogelijk, maar in dit geval $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.